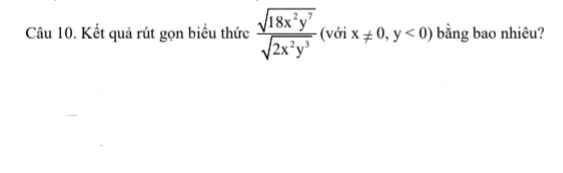a.

\(\lim\limits_{x\rightarrow0}\dfrac{\sqrt{4+x}-2}{4x}=\lim\limits_{x\rightarrow0}\dfrac{\left(\sqrt{4+x}-2\right)\left(\sqrt{4+x}+2\right)}{4x\left(\sqrt{4+x}+2\right)}\)

\(=\lim\limits_{x\rightarrow0}\dfrac{x}{4x\left(\sqrt{4+x}+2\right)}=\lim\limits_{x\rightarrow0}\dfrac{1}{4\left(\sqrt{4+x}+2\right)}=\dfrac{1}{4\left(\sqrt{4+0}+2\right)}=\dfrac{1}{16}\)

b.

\(\lim\limits_{x\rightarrow1}\dfrac{\sqrt[3]{x+7}-2}{x-1}=\lim\limits_{x\rightarrow1}\dfrac{\left(\sqrt[3]{x+7}-2\right)\left(\sqrt[3]{\left(x+7\right)^2}+2\sqrt[3]{x+7}+4\right)}{\left(x-1\right)\left(\sqrt[3]{\left(x+7\right)^2}+2\sqrt[3]{x+7}+4\right)}\)

\(=\lim\limits_{x\rightarrow1}\dfrac{x-1}{\left(x-1\right)\left(\sqrt[3]{\left(x+7\right)^2}+2\sqrt[3]{x+7}+4\right)}=\lim\limits_{x\rightarrow1}\dfrac{1}{\sqrt[3]{\left(x+7\right)^2}+2\sqrt[3]{x+7}+4}\)

\(=\dfrac{1}{\sqrt[3]{8^2}+2\sqrt[3]{8}+4}=\dfrac{1}{12}\)

Lời giải:

$A=1+\frac{1}{\sqrt{x}-3}$

Để $A$ max thì $\sqrt{x}-3$ phải dương và nhỏ nhất. 

Với $x$ nguyên, để $\sqrt{x}-3$ dương và nhỏ nhất thì $x=10$

Khi đó, $A_{\max}=1+\frac{1}{\sqrt{10}-3}=4+\sqrt{10}$

------------------

$B=1+\frac{1}{\sqrt{x}-2}$.

Lập luận tương tự phần a, ta thấy với $x$ nguyên không âm thì $\sqrt{x}-2$ đạt giá trị dương nhỏ nhất tại $x=5$

$\Rightarrow B_{\max}=1+\frac{1}{\sqrt{5}-2}=3+\sqrt{5}$

D

C

ủa vậy đáp án nào ạ??

\(x+y=1\Rightarrow x=1-y\) 

\(C=x^2+y^2+xy=\left(1-y\right)^2+y^2+\left(1-y\right)y\)

\(=y^2-y+1\)\(=\left(y-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall y\)

=>minC=\(\dfrac{3}{4}\) \(\Leftrightarrow y=\dfrac{1}{2}\Rightarrow x=\dfrac{1}{2}\)

Ta có :

\(x+y=1\Rightarrow\left(x+y\right)^2=1\)

\(\Leftrightarrow x^2+2xy+y^2=1\)

\(\Leftrightarrow x^2+xy+y^2=1-xy\ge1-\left(\dfrac{x+y}{2}\right)^2=1-\dfrac{1}{4}=\dfrac{3}{4}\)

Hay \(C \ge \dfrac{3}{4}\)

Dấu "=" xảy ra khi \(x=y=\dfrac{1}{2}\)

D

C

B

D

A

Lời giải:

Gọi chiều dài và chiều rộng ban đầu là $a$ và $a-25$ (m) 

Diện tích ban đầu: $a(a-25)$

Diện tích sau thay đổi: $(a-25)(a-25)$

Theo bài ra: $a(a-25)-(a-25)(a-25)=1000$

$\Leftrightarrow (a-25)[a-(a-25)]=1000$

$\Leftrightarrow 25(a-25)=1000$

$\Leftrightarrow a-25=40$

$\Leftrightarrow a=65$ (m) 

Vậy mảnh đất ban đầu có chiều dài 65 m, chiều rộng 40 m 

\(=\sqrt{9y^4}=3y^2\)