Câu này em đã hỏi rồi

1.Tìm GTNN của Bthức : B= 4x2- 6x+1 : (x-2)2    với x ≠ 22. Tìm GTLN của Bthức: C= x2 + 4x - 14  : x2 -2x +1  với x≠ 1gi... - Hoc24

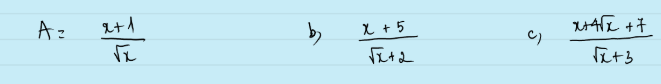
\(A=\sqrt{x}+\dfrac{1}{\sqrt{x}}\ge2\sqrt{\sqrt{x}\cdot\dfrac{1}{\sqrt{x}}}=2\\ A_{min}=2\Leftrightarrow x=1\\ B=\dfrac{x-4+9}{\sqrt{x}+2}=\sqrt{x}-2+\dfrac{9}{\sqrt{x}+2}\\ B=\sqrt{x}+2+\dfrac{9}{\sqrt{x}+2}+4\ge2\sqrt{\left(\sqrt{x}+2\right)\cdot\dfrac{9}{\sqrt{x}+2}}+4\\ B\ge2\sqrt{9}+4=10\\ B_{min}=10\Leftrightarrow\sqrt{x}+2=3\left(\sqrt{x}+2\ge2\right)\Leftrightarrow x=1\)

Áp dụng bất đẳng thức Cô - si ta có:

\(S\) \(=\) \(ab+\dfrac{1}{ab}\ge2\sqrt{ab.\dfrac{1}{ab}}\)

\(S\) \(=\)  \(ab+\dfrac{1}{ab}\ge2\sqrt{1}=2\)

Dấu " = " xảy ra khi \(\left\{{}\begin{matrix}ab=\dfrac{1}{ab}\\a+b=1\end{matrix}\right.\)  ⇔  \(\left\{{}\begin{matrix}\left(ab\right)^2=1\\a+b=1\end{matrix}\right.\)

                                ⇔ \(a=b=0,5\)

GTNN của \(S=ab+\dfrac{1}{ab}=2\) khi \(a=b=0,5\)

S=\(ab+\dfrac{1}{ab}\) 

Ta có :

Áp dụng BĐT Cauchy(cô-sy),ta có

1\(\ge a+b\ge2\sqrt{ab}\)\(\Leftrightarrow\sqrt{ab}\le\dfrac{1}{2}\)\(\Rightarrow ab\le\dfrac{1}{4}\)

Đặt x=ab(x\(\le\dfrac{1}{4}\))

\(\Rightarrow x+\dfrac{1}{x}=x+\dfrac{1}{16x}+\dfrac{15}{16x}\)

Áp dụng BĐT Cauchy (Cô -si):

\(S\ge2\sqrt{\dfrac{1}{16}}+\dfrac{15}{16x}=\dfrac{1}{2}+\dfrac{15}{16X}\ge\dfrac{1}{2}+\dfrac{16}{16.\dfrac{1}{4}}=\dfrac{17}{4}\)

Vậy Min S=\(\dfrac{17}{4}\) \(\Leftrightarrow\left\{{}\begin{matrix}a+b=1\\ab=\dfrac{1}{16ab}\\ab=\dfrac{1}{4}\\\end{matrix}\right.\) \(\Leftrightarrow a=b=\dfrac{1}{2}\)

Lời giải:

Ta thấy: $(x-1)^2\geq 0$ với mọi $x$

$(y+2)^2\geq 0$ với mọi $y$

$\Rightarrow A=(x-1)^2+4(y+2)^2+2021\geq 0+4.0+2021=2021$
Vậy $A_{\min}=2021$. Giá trị đạt được khi $x-1=y+2=0$

$\Rightarrow x=1; y=-2$

Lời giải:

$N=x^2-2xy+2y^2-x=(2y^2-2xy+\frac{x^2}{2})+(\frac{x^2}{2}-x+\frac{1}{2})-\frac{1}{2}$

$=2(y-\frac{x}{2})^2+\frac{1}{2}(x-1)^2-\frac{1}{2}\geq \frac{-1}{2}$

Vậy GTNN của $N$ là $\frac{-1}{2}$

Giá trị này đạt tại $y-\frac{x}{2}=x-1=0$

$\Leftrightarrow x=1; y=\frac{1}{2}$

Ta có: N = x^2 -2xy +2y^2 -x

         2N = 2x^2 - 4xy + 4y^2 - 2x

              = (x^2- 4xy +4y^2) +(x^2 - 2x +1) -1

              = (x-2y)^2 + ( x-1)^2 -1 

=> 2N lớn hơn hoặc bằng -1

=> N lớn hơn hoặc bằng -1/2

   Dấu "=" xảy ra <=> ( x-2y )^2 = 0 và ( x-1 )^2 = 0

                             => x-2y=0 và x-1=0

                             => x=1 và y=1/2

Vậy tại x=1 và y=1/2 thì biểu thức N đạt GTNN là -1/2

tìm GTLN thì đưa về dạng A^2 - k hoặc /A/ -k

GTNN đưa về dạng A^2 + k hoặc /A/ +k

Choi mình VD đi bạn

tìm GTLN của  x^2 - 5

Tìm GTLN của x^2 +1

đấy là các dạng cơ bản. tuy nhiên khi làm , đề bài có thể lắt léo hơn nhưng về cơ bản cuối cùng phải dưa đc về dạng như tui đã bảo

ĐKXĐ: \(\dfrac{3}{2}\le x\le3\)

\(A=\sqrt{2x-3}+\sqrt{6-2x}+\left(2-\sqrt{2}\right)\sqrt{3-x}\)

\(A\ge\sqrt{2x-3+6-2x}+\left(2-\sqrt{2}\right)\sqrt{3-x}\ge\sqrt{3}\)

\(A_{min}=\sqrt{3}\) khi \(3-x=0\Rightarrow x=3\)

\(A=1.\sqrt{2x-3}+\sqrt{2}.\sqrt{6-2x}\le\sqrt{\left(1+2\right)\left(2x-3+6-2x\right)}=3\)

\(A_{max}=3\) khi \(2x-3=\dfrac{6-2x}{2}\Rightarrow x=2\)

x = 2007 and 2008 nha bn