Giups mình với ạ
Giups mình với ạ

Những câu hỏi liên quan
Giups mình bài 9 với ạ!
Mình cần ngay ạ
giups mình với ạ
Bài 1:
\(a,=2\sqrt{3a}-5\sqrt{3a}+\dfrac{1}{2}\cdot4\sqrt{3a}=-3\sqrt{3a}+2\sqrt{3a}=-\sqrt{3a}\\ b,=\dfrac{a+b}{b^2}\cdot\dfrac{\left|a\right|b^2}{\left|a+b\right|}=\dfrac{a+b}{b^2}\cdot\dfrac{\left|a\right|b^2}{a+b}=\left|a\right|\\ c,=5\sqrt{a}-20\left|a\right|b\sqrt{a}+20a\left|b\right|\sqrt{a}-6\sqrt{a}\\ =\left(5\sqrt{a}-6\sqrt{a}\right)-\left(20ab\sqrt{a}-20ab\sqrt{a}\right)\\ =-\sqrt{a}\\ d,=\dfrac{\left(x-\sqrt{3}\right)\left(x+\sqrt{3}\right)}{x+\sqrt{3}}=x-\sqrt{3}\\ e,=\dfrac{\left(1-\sqrt{a}\right)\left(1+\sqrt{a}+a\right)}{1-\sqrt{a}}=1+\sqrt{a}+a\)
Bài 2:
\(a,B=7\sqrt{x+2}-4\sqrt{x+2}-2\sqrt{x+2}=\sqrt{x+2}\\ b,ĐK:x\ge-2\\ PT\Leftrightarrow\sqrt{x+2}=20\Leftrightarrow x+2=400\Leftrightarrow x=398\left(tm\right)\)
Bài 3:
\(a,M=\dfrac{1+\sqrt{a}}{\sqrt{a}\left(\sqrt{a}-1\right)}\cdot\dfrac{\left(\sqrt{a}-1\right)^2}{\sqrt{a}+1}=\dfrac{\sqrt{a}-1}{\sqrt{a}}\\ b,M=\dfrac{\sqrt{a}-1}{\sqrt{a}}=1-\dfrac{1}{\sqrt{a}}< 1\left(\dfrac{1}{\sqrt{a}}>0\right)\)
Đúng 1
Bình luận (0)
Giups mình với ạ
Giups mình với ạ
Giúp gì vậy em! Có gì thì nêu câu hỏi ra nha! Không spam.
Đúng 2
Bình luận (3)

Giups mình với ạ :((((
Bạn ơi, bạn chụp thế thì có nhìn rõ chữ được đâu mà giúp bạn.
Đúng 1
Bình luận (2)
giups mình với ạ :<

Giups mình với ạ!!!
Xét tam giác ABC vuông tại A có AH là đường cao, ta có: \(AB^2=BH.BC=1.\left(1+4\right)=5\Rightarrow AB=\sqrt{5}cm\)
Áp dụng định lí Py-ta-go vào tam giác ABH vuông tại H có:
\(AB^2=BH^2+AH^2\Rightarrow AH^2=AB^2-BH^2=5-1=4\Rightarrow AH=2cm\)
Đúng 1
Bình luận (0)
Ta có: \(BC=BH+HC=1+4=5\left(cm\right).\)
Xét tam giác ABC vuông tại A, AH là đường cao (gt).
\(\Rightarrow AB^2=BH.BC\) (Hệ thức lượng).
\(\Rightarrow AB^2=1.5=5.\\ \Rightarrow AB=\sqrt{5}\left(cm\right).\)
\(AH^2=BH.CH\) (Hệ thức lượng).
\(\Rightarrow AH^2=1.4=4.\\ \Rightarrow AH=2\left(cm\right).\)
Đúng 1
Bình luận (0)
ta có: tam giác ABC vuông tại A, đường cao AH
=>\(AB^2=BH.BC\) ( HTL )
\(\Leftrightarrow AB=\sqrt{1.5}=\sqrt{5}cm\)
ta có:
\(AC^2=CH.CB\left(HTL\right)\)
\(\Leftrightarrow AC=\sqrt{4.5}=\sqrt{20}cm\)
ta lại có:
\(AH.BC=AB.AC\left(HTL\right)\)
\(\Leftrightarrow AH.5=\sqrt{5}.\sqrt{20}\)
\(\Leftrightarrow AH=\dfrac{\sqrt{5.20}}{5}=2cm\)
Đúng 1
Bình luận (0)
Giups mình với ạ!!!!
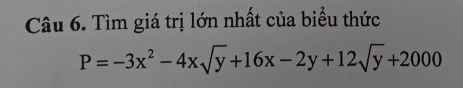
\(P=-3\left(x^2+\dfrac{4}{9}y+\dfrac{64}{9}+\dfrac{4}{3}x\sqrt{y}-\dfrac{16}{3}x-\dfrac{32}{9}\sqrt{y}\right)-\dfrac{2}{3}\left(y-2y+1\right)+2022\)
\(P=-3\left(x+\dfrac{2\sqrt{y}}{3}-\dfrac{8}{3}\right)^2-\dfrac{2}{3}\left(\sqrt{y}-1\right)^2+2022\le2022\)
\(P_{max}=2022\) khi \(\left(x;y\right)=\left(2;1\right)\)
Đúng 1
Bình luận (0)
Giups mình câu này với ạ, mình cmon:(