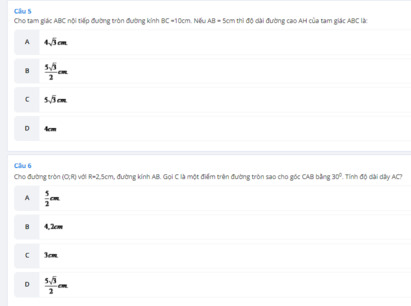
Xét tam giác ABC vuông tại A có AH là đường cao, ta có: \(AB^2=BH.BC=1.\left(1+4\right)=5\Rightarrow AB=\sqrt{5}cm\)
Áp dụng định lí Py-ta-go vào tam giác ABH vuông tại H có:
\(AB^2=BH^2+AH^2\Rightarrow AH^2=AB^2-BH^2=5-1=4\Rightarrow AH=2cm\)
Ta có: \(BC=BH+HC=1+4=5\left(cm\right).\)
Xét tam giác ABC vuông tại A, AH là đường cao (gt).
\(\Rightarrow AB^2=BH.BC\) (Hệ thức lượng).
\(\Rightarrow AB^2=1.5=5.\\ \Rightarrow AB=\sqrt{5}\left(cm\right).\)
\(AH^2=BH.CH\) (Hệ thức lượng).
\(\Rightarrow AH^2=1.4=4.\\ \Rightarrow AH=2\left(cm\right).\)
ta có: tam giác ABC vuông tại A, đường cao AH
=>\(AB^2=BH.BC\) ( HTL )
\(\Leftrightarrow AB=\sqrt{1.5}=\sqrt{5}cm\)
ta có:
\(AC^2=CH.CB\left(HTL\right)\)
\(\Leftrightarrow AC=\sqrt{4.5}=\sqrt{20}cm\)
ta lại có:
\(AH.BC=AB.AC\left(HTL\right)\)
\(\Leftrightarrow AH.5=\sqrt{5}.\sqrt{20}\)
\(\Leftrightarrow AH=\dfrac{\sqrt{5.20}}{5}=2cm\)