Cho tam giác abc đều nội tiếp đường tròn bán kính r=8. tính diện tích tam giác abc.

Những câu hỏi liên quan
Cho tam giác ABC có các cạnh BC = a, CA = b, AB = c. Gọi r là bán kính đường tròn nội tiếp, S là diện tích tam giác ABC.
a) Chứng minh : \(S=\dfrac{r\left(a+b+c\right)}{2}\)
b) Tính bán kính đường tròn nội tiếp của tam giác ABC. Biết tam giác ABC là tam giác cân có cạnh đáy bằng 16 cm, cạnh bên bằng 10 cm.
Hình như câu b chưa rõ lắm, tam giác ABC cân tại đâu?
Đúng 1
Bình luận (1)
Cho tam giác ABC có Â=60° bán kính đường tròn ngoại tiếp , nội tiếp tam giác ABC lần lượt lac R=7/√3 , r=√3. Tính diện tích của ∆ABC
cho tam giác ABC vuông tại A, Gọi r và R lần lượt là bán kính của đường tròn nội tiếp và ngoại tiếp của tam giác ABC. Biết r=5cm, R=37cm. tính diện tích tam giác ABC?
1. Cho tam giác ABC nội tiếp đường tròn tâm O, bán kính R = 3cm. Tính diện tích hình quạt tạo bởi hai bán kính OB,OC và cung nhỏ BC khi \(\widehat{BAC}=60^o\)
2. Cho tam giác ABC vuông tại A có AB=6cm, AC=8cm nội tiếp đường tròn (O). Tính diện tích hình tròn (O)
2: ΔABC vuông tại A nội tiếp (O)
=>O là trung điểm của BC
BC=căn 6^2+8^2=10cm
=>OB=OC=10/2=5cm
S=5^2*3,14=78,5cm2
Đúng 0
Bình luận (0)
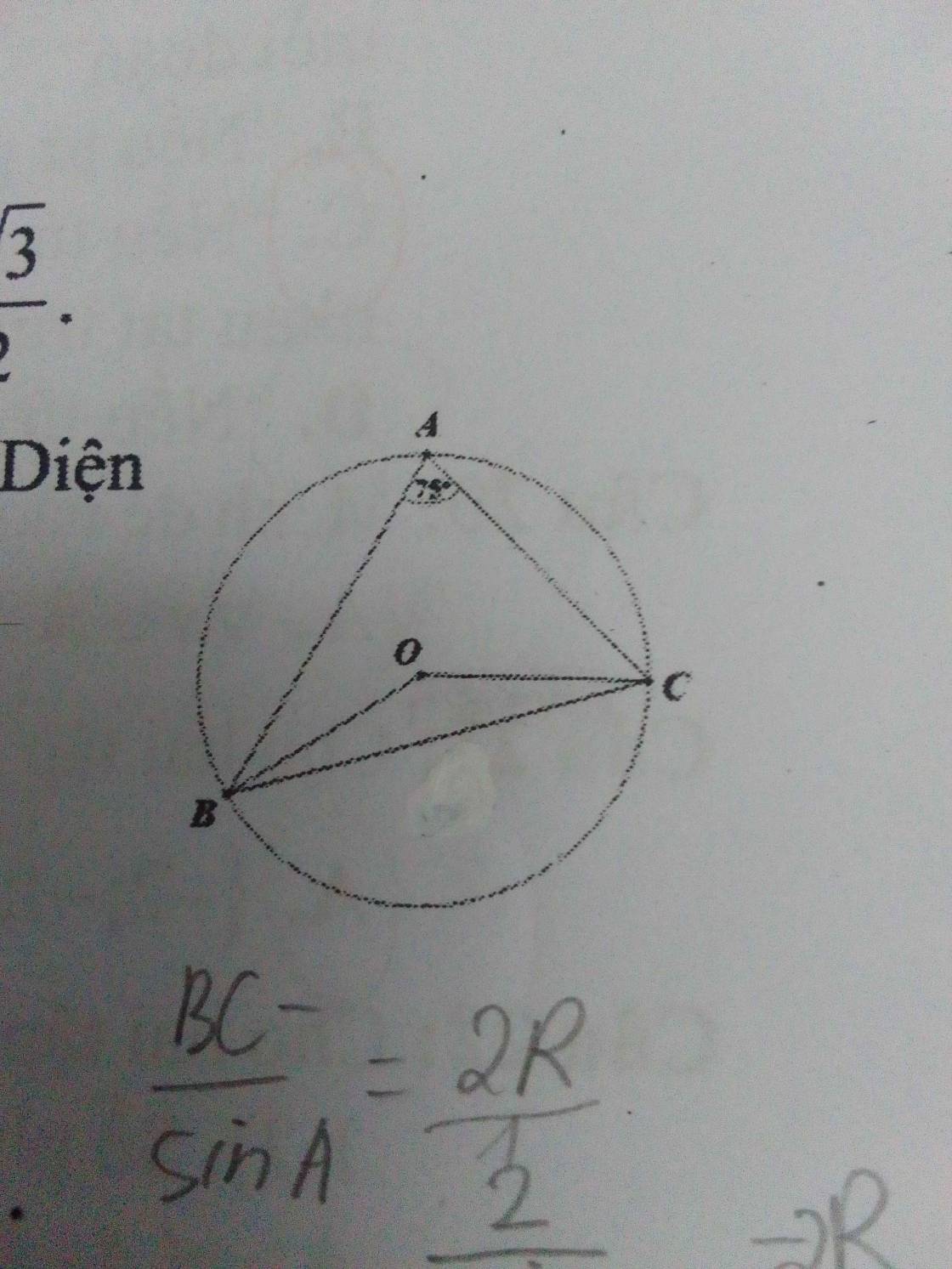 Cho tam giác ABC, góc A=75° nội tiếp đường tròn tâm O bán kính R=1. tính diện tích tam giác OBC.
Cho tam giác ABC, góc A=75° nội tiếp đường tròn tâm O bán kính R=1. tính diện tích tam giác OBC.
Xét (O) có
\(\widehat{BAC}\) là góc nội tiếp chắn cung BC
Do đó: \(\widehat{BAC}=\dfrac{1}{2}\cdot\widehat{BOC}\)
=>\(\widehat{BOC}=75^0:\dfrac{1}{2}=150^0\)
Diện tích tam giác OBC là:
\(S_{OBC}=\dfrac{1}{2}\cdot OB\cdot OC\cdot sinBOC\)
\(=\dfrac{1}{2}\cdot1\cdot1\cdot sin150=\dfrac{1}{4}\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB=8, AC=10,BC=13 A. TÍNH GÓC A B. TÍNH BÁN KÍNH đường tròn nội tiếp tam giác ABC. Tính diện tích tam giác ABC
Xem chi tiết
\(cosA=\dfrac{AB^2+AC^2-BC^2}{2AB.AC}=-\dfrac{1}{32}\)
\(\Rightarrow A\approx92^0\)
\(p=\dfrac{AB+AC+BC}{2}=\dfrac{31}{2}\)
\(S_{ABC}=\sqrt{p\left(p-AB\right)\left(p-AC\right)\left(p-BC\right)}\simeq40\)
\(r=\dfrac{S}{p}=\dfrac{80}{31}\)
Đúng 1
Bình luận (0)
Cho tam giác ABC đều cạnh a nội tiếp đường tròn (O). Tính bán kính đường tròn nội tiếp tam giác ABC. A.
r
a
3
3
B.
r
a
3
2
C.
r
a
3...
Đọc tiếp
Cho tam giác ABC đều cạnh a nội tiếp đường tròn (O). Tính bán kính đường tròn nội tiếp tam giác ABC.
A. r = a 3 3
B. r = a 3 2
C. r = a 3 6
D. r = a 2 3
Chọn đáp án C.
Gọi M là trung điểm của BC: 
Do tam giác ABC đều nên tâm đường tròn nội tiếp tam giác ABC là trọng tâm, tâm đường tròn ngoại tiếp tam giác ABC
Áp dụng định lí Pytago vào tam giác ABM ta có:

Đúng 0
Bình luận (0)
Cho tam giác ABC có a = 12, b = 16, c = 20. Tính diện tích S của tam giác, chiều cao ha, bán kính R, r của các đường tròn ngoại tiếp, nội tiếp tam giác và đường trung tuyến ma của tam giác
Nhận xét: Tam giác ABC có a2 + b2 = c2 nên vuông tại C.
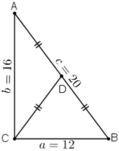
+ Diện tích tam giác: S = 1/2.a.b = 1/2.12.16 = 96 (đvdt)
+ Chiều cao ha: ha = AC = b = 16.
+ Tâm đường tròn ngoại tiếp tam giác là trung điểm của AB.
Bán kính đường tròn ngoại tiếp R = AB /2 = c/2 = 10.
+ Bán kính đường tròn nội tiếp tam giác: S = p.r ⇒ r = S/p.
Mà S = 96, p = (a + b + c) / 2 = 24 ⇒ r = 4.
+ Đường trung tuyến ma:
ma2 = (2.(b2 + c2) – a2) / 4 = 292 ⇒ ma = √292.
Đúng 0
Bình luận (0)
Cho tam giác ABC đều cạnh a nội tiếp đường tròn (O). Tính bán kính R của đường tròn A.
R
a
3
2
B.
R
a
3
3
C.
R
a
2
3...
Đọc tiếp
Cho tam giác ABC đều cạnh a nội tiếp đường tròn (O). Tính bán kính R của đường tròn
A. R = a 3 2
B. R = a 3 3
C. R = a 2 3
D. Đáp án khác
Chọn đáp án B.
Do O là tâm của đường tròn ngoại tiếp tam giác đều ABC nên O đồng thời là trọng tâm tam giác ABC.
Gọi M là trung điểm BC:

Đúng 0
Bình luận (0)















