không giải hệ cho biết số nghiệm của hệ
a,2x-y=3 và x+y=1
b,1/3x+y=5 và x+3y=2
Không cần vẽ hình, hãy cho biết số nghiệm của mỗi hệ phương trình sau đây và giải thích vì sao:
a ) y = 3 − 2 x y = 3 x − 1 b ) y = − 1 2 x + 3 y = − 1 2 x + 1 c ) 2 y = − 3 x 3 y = 2 x d ) 3 x − y = 3 x − 1 3 y = 1
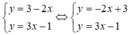
a) Xét (d): y = -2x + 3 có a = -2; b = 3
(d’) : y = 3x – 1 có a’ = 3 ; b’ = -1.
Có a ≠ a’ ⇒ (d) cắt (d’)
⇒ Hệ 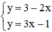 có nghiệm duy nhất.
có nghiệm duy nhất.
b) 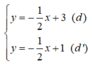
Xét (d): 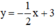 có a =
có a = 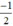 ; b = 3
; b = 3
(d’): 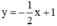 có a’ =
có a’ = 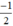 ; b’ = 1.
; b’ = 1.
Có a = a’; b ≠ b’ ⇒ (d) // (d’)
⇒ Hệ phương trình 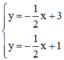 vô nghiệm.
vô nghiệm.
c) Ta có: 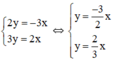
Xét (d): y = 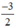 x có a =
x có a = 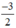 ; b = 0
; b = 0
(d’) : y = 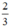 x có a’ =
x có a’ = 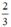 ; b’ = 0
; b’ = 0
Ta có: a ≠ a’ ⇒ (d) cắt (d’)
⇒ Hệ 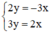 có nghiệm duy nhất.
có nghiệm duy nhất.
d) Ta có:
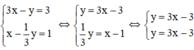
Ta có: a = a’=3; b = b’ = -3
Nhận thấy hai đường thẳng trên trùng nhau
⇒ Hệ phương trình có vô số nghiệm.
Kiến thức áp dụng
+ Xét hệ (I): 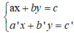
Gọi (d): ax + by = c và (d’): a’x + b’y = c’.
Số nghiệm của hệ (I) phụ thuộc vào vị trí tương đối của (d) và (d’).
(d) cắt (d’) ⇒ hệ (I) có nghiệm duy nhất.
(d) // (d’) ⇒ hệ (I) vô nghiệm
(d) ≡ (d’) ⇒ hệ (I) có vô số nghiệm.
+ Cho đường thẳng (d): y = ax + b và (d’): y = a’x + b’.
(d) cắt (d’) ⇔ a ≠ a’
(d) // (d’) ⇔ a = a’ và b ≠ b’
(d) trùng (d’) ⇔ a = a’ và b = b’.
1) {x^2+2x^2=3 {2x^2+3x^2=5 2) giải theo m {x+y=2m+1 {x-y=1 3)giải theo m {x +2y=3m+2 {2x+y=3m+2 4) cho hệ. {x+3y=4m+4 {2x+y=3m+3 Tìm m để hệ có nghiệm (x,y) thỏa mãn x+y=4 HỆ PHƯƠNG TRÌNH HẾT Ạ Giúp mik với nhé
4:
x+3y=4m+4 và 2x+y=3m+3
=>2x+6y=8m+8 và 2x+y=3m+3
=>5y=5m+5 và x+3y=4m+4
=>y=m+1 và x=4m+4-3m-3=m+1
x+y=4
=>m+1+m+1=4
=>2m+2=4
=>2m=2
=>m=1
3:
x+2y=3m+2 và 2x+y=3m+2
=>2x+4y=6m+4 và 2x+y=3m+2
=>3y=3m+2 và x+2y=3m+2
=>y=m+2/3 và x=3m+2-2m-4/3=m+2/3
giải các hệ phương trình
9x-6y=4 và 3(4x-3y)=-3x+y+7
3(x+1)+2y=-x và 5(x+y)=-3x+y-5
2(2x+3y)=3(2x-3y)+10 và 4x-3y=4(6y-2x)+3
Bài 1 Cho hệ phương trình mx+4y=10-m và x+y=4
a, giải hệ phương trình khi m= căn 2
b, giải và biện luận hệ phương trình đã cho theo tham số m
c, trong trường hợp hệ có nghiệm duy nhất (x;y) tìm các giá trị của m để:
i, y-5x=-4. ii, x<1 và y>0
Bài 2: Cho hệ phương trình 2x+3y=m và 2x-3y=6 (m là tham số không âm)
a, giải hệ phương trình với m=3
b, tìm các giá trị của m để nghiệm (x;y) của hệ phương trình thoả mãn điều kiện x>0, y>0
GIẢI HỆ PHƯƠNG TRÌNH ( Mình không gõ được hệ phương trình nên trong một câu mình để hai phương trình, các bạn tự hiểu là hệ phương trình )
1,
( 1 / x + y ) + ( 1 / x - y ) = 5 / 8
( 1 / x + y ) - ( 1 / x - y ) = - 3 / 8
2,
( 4 / 2x - 3y ) + ( 5 / 3x + y ) = - 2
( 3 / 3x + y ) - ( 5 / 2x + 3y ) = 21
MÌNH ĐANG CẦN GẤP GIÚP MÌNH NHÉ MÌNH SẼ TICK NHANH CHO BẠN NÀO GIẢI ĐẦY ĐỦ VÀ NHANH 😭😭😭
Ta có: \(\hept{\begin{cases}\left(\frac{1}{x}+y\right)+\left(\frac{1}{x}-y\right)=\frac{5}{8}\\\left(\frac{1}{x}+y\right)-\left(\frac{1}{x}-y\right)=-\frac{3}{8}\end{cases}\Leftrightarrow\hept{\begin{cases}\frac{2}{x}=\frac{5}{8}\\2y=-\frac{3}{8}\end{cases}\Leftrightarrow}\hept{\begin{cases}x=\frac{16}{5}\\y=-\frac{3}{16}\end{cases}}}\)
1. Cho hệ phương trình \(\left\{{}\begin{matrix}2x-y=m-1\\3x+y=4m+1\end{matrix}\right.\) (m là tham số)
a) Giải hệ phương trình vớim=2
b) Tìm m để hệ phương trình có nghiệm duy nhất (x;y) thỏa mãn \(2x^2-3y=2\)
Bài 1: Cho hpt \(\left\{{}\begin{matrix}x+2y=m+3\\2x-3y=m\end{matrix}\right.\) ( m là tham số)
a) Giải hệ phương trình m=1
b) Tìm m để hệ phương trình có nghiệm duy nhất thỏa mãn: x + y = 3
(mink đag cần gấp)
a)
Khi m = 1, ta có:
{ x+2y=1+3
2x-3y=1
=> { x+2y=4
2x-3y=1
=> { 2x+4y=8
2x-3y=1
=> { x+2y=4
2x-3y-2x-4y=1-8
=> { x=4-2y
-7y = -7
=> { x = 2
y = 1
Vậy khi m = 1 thì hệ phương trình có cặp nghệm
(x; y) = (2;1)
a) Thay m=1 vào HPT ta có:
\(\left\{{}\begin{matrix}x+2y=4\\2x-3y=1\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}2x+4y=8\\2x-3y=1\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}2x+4y=8\\7y=7\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)
Vậy HPT có nghiệm (x;y)= (2;1)
Bài 1: Cho hpt \(\left\{{}\begin{matrix}x+2y=m+3\\2x-3y=m\end{matrix}\right.\) ( m là tham số)
a) Giải hệ phương trình m=1
b) Tìm m để hệ phương trình có nghiệm duy nhất thỏa mãn: x + y = 3
(mink đag cần gấp)
a) Thay m=1 vào hệ phương trình, ta được:
\(\left\{{}\begin{matrix}x+2y=4\\2x-3y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+4y=8\\2x-3y=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}7y=7\\x+2y=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=1\\x=4-2y=4-2=2\end{matrix}\right.\)
Vậy: Khi m=1 thì hệ phương trình có nghiệm duy nhất là (x,y)=(2;1)
b) Ta có: \(\left\{{}\begin{matrix}x+2y=m+3\\2x-3y=m\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=m+3-2y\\2\left(m+3-2y\right)-3y=m\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=m+3-2y\\2m+6-4y-3y-m=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=m+3-2y\\-7y+m+6=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=m+3-2y\\-7y=-m-6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=m+3-2y\\y=\dfrac{m+6}{7}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=m+3-2\cdot\dfrac{m+6}{7}\\y=\dfrac{m+6}{7}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=m+3-\dfrac{2m+12}{7}\\y=\dfrac{m+6}{7}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{7m+21-2m-12}{7}=\dfrac{5m+9}{7}\\y=\dfrac{m+6}{7}\end{matrix}\right.\)
Để hệ phương trình có nghiệm duy nhất thỏa mãn x+y=3 thì \(\dfrac{5m+9}{7}+\dfrac{m+6}{7}=3\)
\(\Leftrightarrow6m+15=21\)
\(\Leftrightarrow6m=6\)
hay m=1
Vậy: Khi m=1 thì hệ phương trình có nghiệm duy nhất thỏa mãn x+y=3
a/ Thay \(m=1\) vào hpt ta có :
\(\left\{{}\begin{matrix}x+2y=4\\2x-3y=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)
Vậy...
b/ Ta có :
\(\left\{{}\begin{matrix}x+2y=m+3\\2x-3y=m\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{m+3}{2y}\\\dfrac{2\left(m+3\right)}{2y}-3y=m\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{m+3}{2y}\\\dfrac{m+3}{y}-3y=m\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{m+3}{2y}\\m-3y^2+3=my\end{matrix}\right.\)
Cho hệ phương trình (IV) :
3x-y=2m-1 và x+2y=3m+2
a, Gỉai hpt ( IV) khi m=1
b, Tìm m đề hpt (IV) có nghiệm duy nhất (x;y) sao cho :x^2+y^2=5
c, Tìm m để hpt có nghiệm duy nhất x;y sao cho x-3y>0