Trong bóng đá đúng ko em

Câu 1 

+Lấy đà

+tung bóng lên cao

Câu 2

giúp bóng bay vs lực mạnh hơn

 Câu 1: Có 4 giai đoạn: chuẩn bị, chạy đà,ra sức và cuối cùng là giữ thăng bằng

Câu 2 : Có tác dụng để ném bóng được xa hơn,tăng thêm uy lực tấn công

Tham khảo

Thông thường thì hướng di chuyển của bạn sẽ là từ cánh phải hoặc cánh trái của đối phương. Kỹ thuật ném bóng rổ 2 bước được thực hiện qua hai bước chính là chạy đà và ném bóng vào rổ

2?

2 bước

Sau khi chạy hết một còng chiều dài đoạn đường chạy mà vận động viên đã hoàn thành là :

               \(\left(64+109\right)\times2=346\left(m\right)\)

Vậy............

Số m chiều dài đoạn đường chạy mà vđv đã hoàn thành 1 vòng :

\(\left(64+109\right).2=346\left(m\right)\)

Đáp số...

Một vòng nha bạn.

Câu C nha

C

C

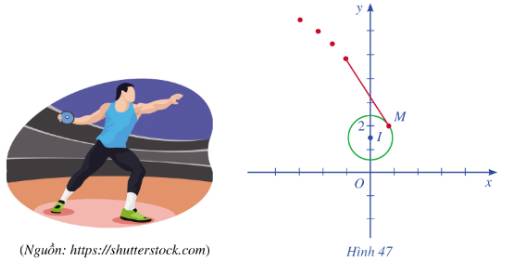
Sau khi được ném đi, quỹ đạo chuyển động của chiếc đĩa nằm trên tiếp tuyến của đường tròn tâm I tại điểm M.

Vậy quỹ đạo chuyển động của chiếc đĩa nằm trên đường thẳng có phương trình là:

\(\begin{array}{l}\left( {\frac{{\sqrt {39} }}{{10}} - 0} \right)\left( {x - \frac{{\sqrt {39} }}{{10}}} \right) + \left( {2 - \frac{3}{2}} \right)\left( {y - 2} \right) = 0\\ \Leftrightarrow \frac{{\sqrt {39} }}{{10}}\left( {x - \frac{{\sqrt {39} }}{{10}}} \right) + \frac{1}{2}\left( {y - 2} \right) = 0\\ \Leftrightarrow \sqrt {39} x + 5y - 13,9 = 0\end{array}\)

Sau khi được ném đi, quỹ đạo chuyển động của chiếc đĩa nằm trên tiếp tuyến của đường tròn tâm I tại điểm M.

Vậy quỹ đạo chuyển động của chiếc đĩa nằm trên đường thẳng có phương trình là:

\(\left(\dfrac{\sqrt{39}}{10}-0\right)\left(x-\dfrac{\sqrt{39}}{10}\right)+\left(2-\dfrac{3}{2}\right)\left(y-2\right)=0\\ \Leftrightarrow\dfrac{\sqrt{39}}{10}\left(x-\dfrac{\sqrt{39}}{10}\right)+\dfrac{1}{2}\left(y-2\right)=0\\ \Leftrightarrow\sqrt{39}x+5y-13,9=0\)

em ko biết

hi hi

Tham khảo:

Tầm xa đạt lớn nhất ↔ \(L = \)\(\dfrac{v_0^2.\sin2\alpha}{g}\)  lớn nhất

↔ \(\sin2\alpha=1\)

↔\(\alpha=45^0\)

Hay \(L \) lớn nhất = \(\dfrac{v^2_0}{g}=60\)

↔ \(v_0^2=60g\)

Tương tự, \(H\) lớn nhất = \(\dfrac{v_0^2}{2g}\), thay số:

\(H \) max \(=\dfrac{60g}{2g}=30\left(m\right)\)