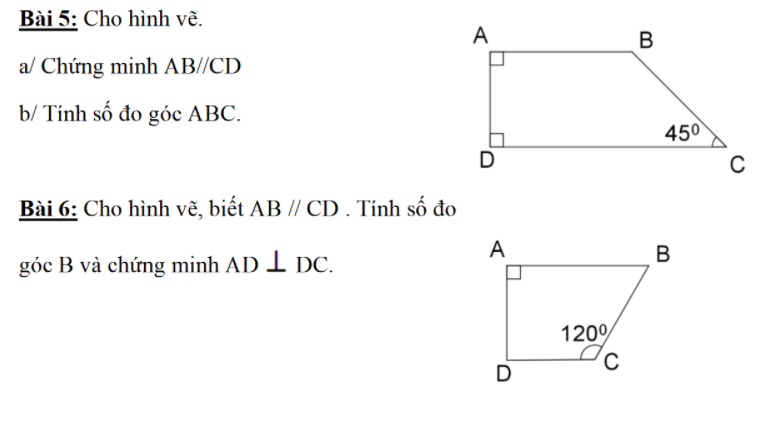
Bài 5:

a) Ta có: AB⊥AD,DC⊥AD

=> AB//DC

b) Ta có: AB//DC

\(\Rightarrow\widehat{ABC}+\widehat{C}=180^0\)(trong cùng phía)

\(\Rightarrow\widehat{ABC}=180^0-45^0=135^0\)

Bài 6:

a) Ta có: AB//CD

\(\Rightarrow\widehat{B}+\widehat{C}=180^0\)(trong cùng phía)

\(\Rightarrow\widehat{B}=180^0-120^0=60^0\)

Ta có: AB//CD,AB⊥AD

=> AD⊥DC

Bài 8:

a) \(\widehat{ACD}+\widehat{C}=180^0\)(kề bù)

\(\Rightarrow\widehat{ACD}=180^0-55^0=125^0\)

b) Ta có: \(\widehat{C}+\widehat{D}=55^0+125^0=180^0\)

Mà 2 góc này trong cùng phía

=> AC//BD

c) Ta có: AC//BD,AC⊥AB

=> AB⊥BD 

Sao không có gì hết vậy?

cái gì mới đc chứ bn

thiếu câu hỏi r bn

a: Xét ΔBAE và ΔBDE có

BA=BD

\(\widehat{ABE}=\widehat{DBE}\)

BE chung

Do đó: ΔBAE=ΔBDE

b: Ta có: ΔBAE=ΔBDE

nên \(\widehat{BAE}=\widehat{BDE}=90^0\)

hay ED\(\perp\)BC

c: Xét ΔAKE vuông tại A và ΔDCE vuông tại D có

EA=ED

\(\widehat{AEK}=\widehat{DEC}\)

Do đó: ΔAKE=ΔDCE
Suy ra: EK=EC
hay ΔEKC cân tại E

a)\(R_1//R_2\Rightarrow R_{12}=\dfrac{R_1\cdot R_2}{R_1+R_2}=\dfrac{60\cdot40}{60+40}=24\Omega\)

\(I=\dfrac{U}{R_{tđ}}=\dfrac{12}{24}=0,5A\)

b)\(U_1=U_2=U=12V\)

\(P_1=\dfrac{U_1^2}{R_1}=\dfrac{12^2}{60}=2,4W\)

\(P_2=\dfrac{U_2^2}{R_2}=\dfrac{12^2}{40}=3,6W\)

c)CTM mới: \(R_3nt(R_1//R_2)\)

\(I'=\dfrac{I}{2}=\dfrac{0,5}{2}=0,25A\)

\(R_{tđ}=\dfrac{U}{I'}=\dfrac{12}{0,25}=48\Omega\)

\(R_3=R_{tđ}-R_{12}=48-24=24\Omega\)

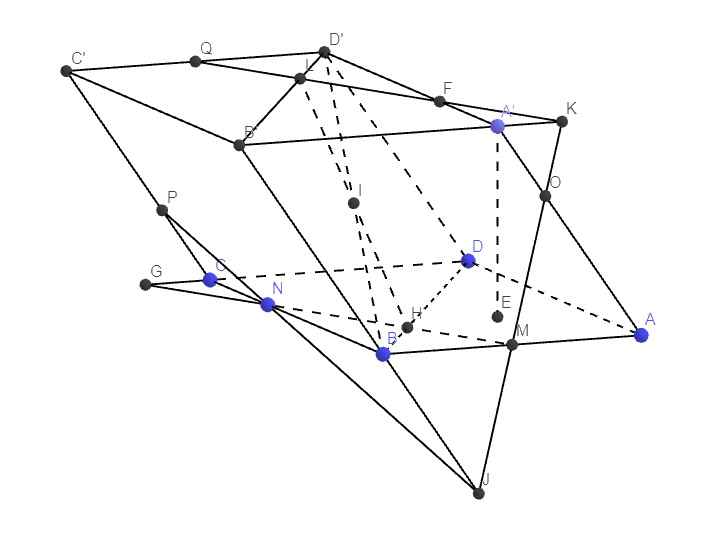
Từ đề bài ta suy ra tất cả các mặt bên của hộp đều là hình thoi (được ghép từ 2 tam giác đều)

\(\Rightarrow A'D=A'B=A'A=a\Rightarrow\) hình chiếu vuông góc của A' lên (ABCD) trùng trọng tâm E của tam giác ABD

\(\widehat{DBE}=\dfrac{1}{2}.60^0=30^0\Rightarrow\widehat{CBE}=\widehat{CBD}+\widehat{DBE}=60^0+30^0=90^0\)

\(\Rightarrow BC\perp BE\)

Mà \(A'E\perp\left(ABCD\right)\Rightarrow A'E\perp BC\)

\(\Rightarrow BC\perp\left(A'BE\right)\Rightarrow BC\perp A'B\)

\(\Rightarrow B'C'\perp A'B\)

\(AE=\dfrac{2}{3}.\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{3}\Rightarrow A'E=\sqrt{A'A^2-AE^2}=\dfrac{a\sqrt{6}}{3}\)

Qua C' dựng đường thẳng song song A'E cắt AC tại F \(\Rightarrow C'F=A'E=\dfrac{a\sqrt{6}}{3}\)

\(CF=AE=\dfrac{a\sqrt{3}}{3}\) ; \(AC=2.\dfrac{a\sqrt{3}}{2}=a\sqrt{3}\Rightarrow AF=AC+CF=\dfrac{4a\sqrt{3}}{3}\)

\(\Rightarrow AC'=\sqrt{AF^2+C'F^2}=a\sqrt{6}\)

\(CP=\dfrac{1}{3}CC'\) ; \(CN=\dfrac{1}{3}BC\)

Nối PN kéo dài cắt BB' tại J

Talet: \(\dfrac{CP}{BJ}=\dfrac{CN}{NB}=\dfrac{1}{2}\Rightarrow BJ=2CP=\dfrac{2a}{3}\Rightarrow\dfrac{BJ}{B'J}=\dfrac{\dfrac{2a}{3}}{a+\dfrac{2a}{3}}=\dfrac{2}{5}\)

Nối JM cắt A'B' kéo dài tại K

Talet: \(\dfrac{BM}{B'K}=\dfrac{BJ}{B'J}=\dfrac{2}{5}\Rightarrow B'K=\dfrac{5BM}{2}=\dfrac{5a}{4}\)

Nối MN cắt BD tại H và cắt CD tại G

Talet: \(\dfrac{CG}{BM}=\dfrac{CN}{BN}=\dfrac{1}{2}\Rightarrow CG=\dfrac{1}{2}BM=\dfrac{a}{4}\Rightarrow DG=a+\dfrac{a}{4}=\dfrac{5a}{4}\)

Talet: \(\dfrac{BH}{DH}=\dfrac{BM}{DG}=\dfrac{a\div2}{5a\div4}=\dfrac{2}{5}\) (1)

Nối GP cắt C'D' tại Q

Talet: \(\dfrac{CG}{C'Q}=\dfrac{CP}{C'P}=\dfrac{1}{2}\Rightarrow C'Q=2CG=\dfrac{a}{2}\)

Nối QK cắt B'D' tại L

Talet: \(\dfrac{D'L}{B'L}=\dfrac{D'Q}{B'K}=\dfrac{a\div2}{5a\div4}=\dfrac{2}{5}\) (2)

(1);(2) \(\Rightarrow D'L=BH\) (do \(BD=B'D'\))

Nối HL cắt BD' tại I

Talet: \(\dfrac{D'I}{IB}=\dfrac{D'L}{BH}=1\)

Gọi F là giao điểm QK và A'D', O là giao điểm JK và A'A

Ta đồng thời suy ra luôn NPQFOM là thiết diện của (MNP) và chóp

8 It took me 3 hours to do these exercise

9 Many years ago, my village used to be very poor

10 Mary last met him 5 years ago

11 Would you mind giving me a hand

12 There used to be many old buildings in this city

13 When were they married

14 I started learning Japanese 2 years ago

15 Jack used to be a good student

16  My sister used to buy all her clothes in Henry's

17 Braille is reading system for the blind

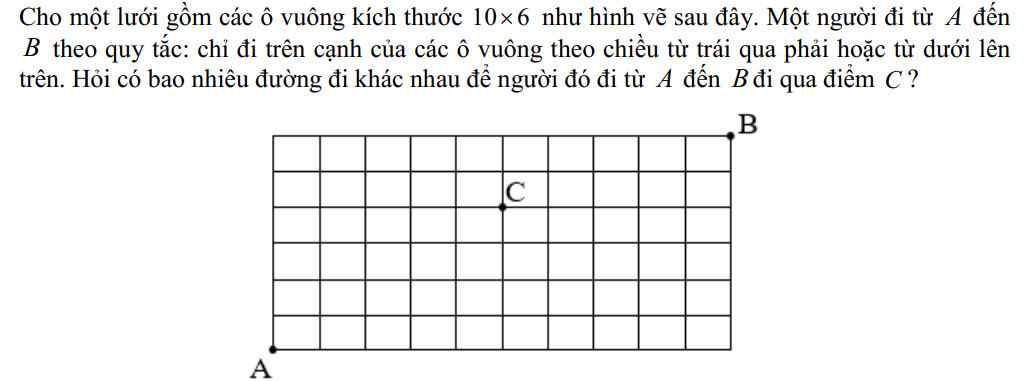
Từ A đến C, có 4 đoạn đi lên (nằm song song nhau) và 5 đoạn đi ngang nằm song song

Ta kí hiệu đi lên là L và đi ngang là N, như vậy, số cách đi từ A đến C là số cách sắp xếp 9 kí tự bao gồm 4L và 5N

\(\Rightarrow\) Có \(\dfrac{9!}{5!.4!}\) cách

Tương tự, từ C đến B có 2L và 5N, có \(\dfrac{7!}{2!.5!}\) cách

Tổng cộng: \(\dfrac{9!}{5!.4!}.\dfrac{7!}{2!.5!}\) cách đi từ A đến B

Cách làm ngắn gọn: \(5=\dfrac{5\left(x-1\right)}{x-1}=\dfrac{5x-5}{x-1}=\dfrac{5x+5-10}{x-1}\)

Do đó chọn \(f\left(x\right)=5x+5\) thế vào nhanh chóng tính ra kết quả giới hạn

Còn cách khác phức tạp hơn (có thể sử dụng cho tự luận):

Do \(\lim\limits_{x\rightarrow1}\dfrac{f\left(x\right)-10}{x-1}=5\) hữu hạn nên \(f\left(x\right)-10=0\) có nghiệm \(x=1\)

\(\Rightarrow f\left(1\right)-10=0\Rightarrow f\left(1\right)=10\)

Do đó:

\(\lim\limits_{x\rightarrow1}\dfrac{f\left(x\right)-10}{\left(\sqrt{x}-1\right)\left(\sqrt{4f\left(x\right)+9}+3\right)}=\lim\limits_{x\rightarrow1}\dfrac{\left[f\left(x\right)-10\right]\left(\sqrt{x}+1\right)}{\left(x-1\right)\left(\sqrt{4f\left(x\right)+9}+3\right)}\)

\(=\lim\limits_{x\rightarrow1}\dfrac{f\left(x\right)-10}{x-1}.\dfrac{\sqrt{x}+1}{\sqrt{4f\left(x\right)+9}+3}=5.\dfrac{1+1}{\sqrt{4f\left(1\right)+9}+3}=5.\dfrac{2}{\sqrt{4.10+9}+3}=...\)