Phân tích đa thức thành nhân tử:
a) 3x² – 6x
b) x² + 4x – 25y² + 4
c) 2x² – 5x – 3
Phân tích các đa thức sau thành nhân tử:
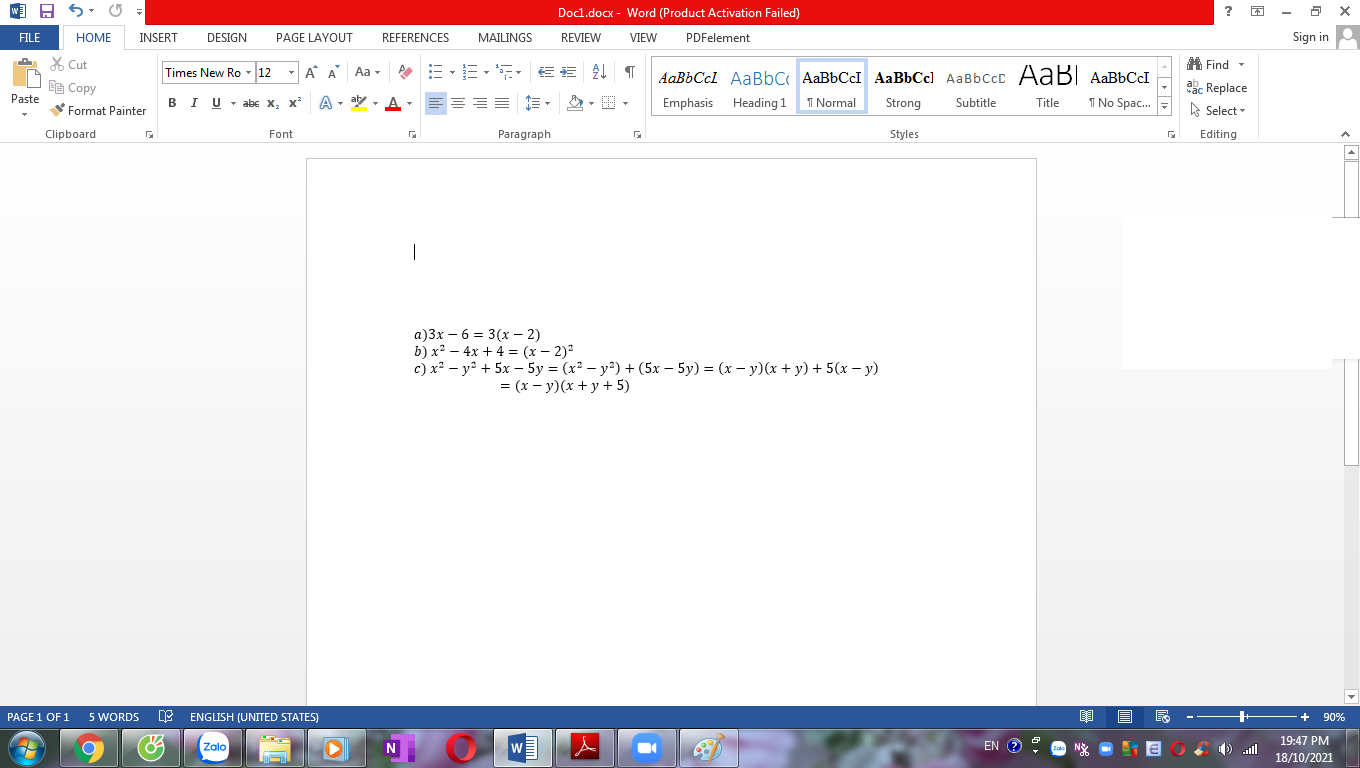
a) 3x-6
b) x2-4x+4
c) x2-y2+5x-5y
d) 8(x+y+z)3-(x+y)3-(y+z)3-(y+z)3-(z+x)3
Do câu d mình ko biết làm bởi v mình không làm được
1A. Phân tích các đa thức sau thành nhân tử:
a) x3+2x; b) 3x - 6y;
c) 5(x + 3y)- 15x(x + 3y); d) 3(x-y)- 5x(y-x).
1B. Phân tích các đa thức sau thành nhân tử:
a) 4x2 - 6x; b) x3y - 2x2y2 + 5xy;
![]()
![]() c) 2x2(x +1) + 4x(x +1); d) 2 x(y - 1) - 2
c) 2x2(x +1) + 4x(x +1); d) 2 x(y - 1) - 2
y(1 - y).
5 5
2A. Phân tích các đa thức sau thành nhân tử: a) 2(x -1)3 - 5(x -1)2 - (x - 1);
b) x(y - x)3 - y(x - y)2 + xy(x - y);
c) xy(x + y)- 2x - 2y;
d) x(x + y)2 - y(x + y)2 + y2 (x - y).
2B. Phân tích đa thức thành nhân tử: a) 4(2-x)2 + xy - 2y;
b) x(x- y)3 - y(y - x)2 - y2(x - y);
c) x2y-xy2 - 3x + 3y;
d) x(x + y)2 - y(x + y) 2 + xy - x 2 .
1A:
a: \(x^3+2x=x\left(x^2+2\right)\)
b: \(3x-6y=3\left(x-2y\right)\)
c: \(5\left(x+3y\right)-15x\left(x+3y\right)\)
\(=5\left(x+3y\right)\left(1-3x\right)\)
d: \(3\left(x-y\right)-5x\left(y-x\right)\)
\(=3\left(x-y\right)+5x\left(x-y\right)\)
\(=\left(x-y\right)\left(5x+3\right)\)
1A. a. x(x2+2)
b. 3(x-2y)
c. 5(x+3y)(1-3x)
d. (x-y) (3-5x)
1B. a. 2x(2x-3)
b.xy(x2-2xy+5)
c. 2x(x+1)(x+2)
d. 2x(y-1)+2y(y-1)=2(y-1)(x-y)
1B:
a: \(4x^2-6x=2x\left(2x-3\right)\)
b: \(x^3y-2x^2y^2+5xy\)
\(=xy\left(x^2-2xy+5\right)\)
Phân tích các đa thức sau thành nhân tử:
a) x^{3}-3x^{2}y+4x-12y
b) 4x^{2}-y^{2}+4y-4
c) 9x^{2}-6x-y^{2}+2y
a) $x^3-3x^2y+4x-12y$
$=(x^3-3x^2y)+(4x-12y)$
$=x^2(x-3y)+4(x-3y)$
$=(x-3y)(x^2+4)$
b) $4x^2-y^2+4y-4$
$=4x^2-(y^2-4y+4)$
$=(2x)^2-(y^2-2\cdot y\cdot2+2^2)$
$=(2x)^2-(y-2)^2$
$=[2x-(y-2)][2x+(y-2)]$
$=(2x-y+2)(2x+y-2)$
c) $9x^2-6x-y^2+2y$
$=(9x^2-y^2)-(6x-2y)$
$=[(3x)^2-y^2]-2(3x-y)$
$=(3x-y)(3x+y)-2(3x-y)$
$=(3x-y)(3x+y-2)$
$\text{#}Toru$
tính:
a) \(3x^2\left(2x-1\right)\)
phân tích đa thức thành nhân tử:
a) \(5x^2-10x\)
b) \(4x^2-y^2-4x+1\)
a) \(=5x\left(x-2\right)\)
b) \(=\left(2x\right)^2-2x.2+1-y^2=\left(2x-1\right)^2-y^2=\left(2x-1-y\right)\left(2x-1+y\right)\)
1/
a) 3x2(2x−1)
= 6x3-3x2
2/
a) \(5x^2-10x\)
= \(5x\left(x-2\right)\)
b) \(4x^2-y^2-4x+1\)
= \(4x^2-4x+1-y^2\)
= \(\left(2x-1\right)^2-y^2\)
= \(\left(2x-1-y\right)\left(2x-1+y\right)\)
a) \(3x^2\left(2x-1\right)=6x^3-3x^2.\)
a) \(5x^2-10x=5x\left(x-2\right).\)
b) \(4x^2-y^2-4x+1=\left(2x-1\right)^2-y^2=\left(2x-1-y\right)\left(2x-1+y\right).\)
Phân tích các đa thức sau thành nhân tử:
a,x3+4x-5
b,x3-3x2+4
c,x3+2x2+3x+2
d,x2+2xy+y2+2x-2y-3
e,(x2+3x)2-2(x2+3x)-8
f,(x2+4x+10)2-7(x2+4x+11)+7
a) x3+4x-5 = x3-x2+x2+4x-5=(x3-x2)+(x2-x)+(5x-5)=x2(x-1)+x(x-1)+5(x-1)=(x2+x+5)(x-1)
b) x3-3x2+4=x3-2x2-x2+4=(x3-2x2)-(x2-4)=x2(x-2)-(x-2)(x+2)=(x2-x+2)(x-2)
c) x3+2x2+3x+2=x3+x2+x2+x+2x+2=(x3+x2)+(x2+x)+(2x+2)=x2(x+1)+x(x+1)+2(x+1)=(x2+x+2)(x+1)
d) bạn xem lại đề đúng ko
e) (x2+3x)2-2(x2+3x)-8=x4+6x3+9x2-2x2-6x-8=x4+6x3+7x2-6x-8=x4-x3+7x3-7x2+14x2-14x+8x-8=(x4-x3)+(7x3-7x2)+(14x2-14x)+(8x-8)=x3(x-1)+7x2(x-1)+14x(x-1)+8(x-1)=(x3+7x2+14x+8)(x-1)=(x3+x2+6x2+6x+8x+8)(x-1)=\(\left[\left(x^3+x^2\right)+\left(6x^2+6x\right)+\left(8x+8\right)\right]\left(x-1\right)\)\(=\left[x^2\left(x+1\right)+6x\left(x+1\right)+8\left(x+1\right)\right]\left(x-1\right)\)\(=\left(x^2+6x+8\right)\left(x+1\right)\left(x-1\right)\)\(=\left(x^2+2x+4x+8\right)\left(x+1\right)\left(x-1\right)\)\(=\left[\left(x^2+2x\right)+\left(4x+8\right)\right]\left(x+1\right)\left(x-1\right)\)\(=\left[x\left(x+2\right)+4\left(x+2\right)\right]\left(x+1\right)\left(x-1\right)\)=\(\left(x-1\right)\left(x+1\right)\left(x+2\right)\left(x+4\right)\)
f) (x2+4x+10)2-7(x2+4x+11)+7=(x2+4x+10)2-\(\left[7\left(x^2+4x+11\right)-7\right]\)\(=\left(x^2+4x+10\right)^2-7\left(x^2+4x+10\right)\)\(=\left(x^2+4x+10\right)\left(x^2+4x+3\right)\)
a) Ta có: \(x^3+4x-5\)
\(=x^3-x+5x-5\)
\(=x\left(x-1\right)\left(x+1\right)+5\left(x-1\right)\)
\(=\left(x-1\right)\left(x^2+x+5\right)\)
b) Ta có: \(x^3-3x^2+4\)
\(=x^3+x^2-4x^2+4\)
\(=x^2\left(x+1\right)-4\left(x-1\right)\left(x+1\right)\)
\(=\left(x+1\right)\left(x^2-4x+4\right)\)
\(=\left(x+1\right)\cdot\left(x-2\right)^2\)
c) Ta có: \(x^3+2x^2+3x+2\)
\(=x^3+x^2+x^2+x+2x+2\)
\(=x^2\left(x+1\right)+x\left(x+1\right)+2\left(x+1\right)\)
\(=\left(x+1\right)\left(x^2+x+2\right)\)
d) Ta có: \(x^2+2xy+y^2+2x+2y-3\)
\(=\left(x+y\right)^2+2\left(x+y\right)-3\)
\(=\left(x+y\right)^2+3\left(x+y\right)-\left(x+y\right)-3\)
\(=\left(x+y\right)\left(x+y+3\right)-\left(x+y+3\right)\)
\(=\left(x+y+3\right)\left(x+y-1\right)\)
e) Ta có: \(\left(x^2+3x\right)^2-2\left(x^2+3x\right)-8\)
\(=\left(x^2+3x\right)^2-4\left(x^2+3x\right)+2\left(x^2+3x\right)-8\)
\(=\left(x^2+3x\right)\left(x^2+3x-4\right)+2\left(x^2+3x-4\right)\)
\(=\left(x^2+3x-4\right)\left(x^2+3x+2\right)\)
\(=\left(x+4\right)\left(x-1\right)\left(x+1\right)\left(x+2\right)\)
f) Ta có: \(\left(x^2+4x+10\right)^2-7\left(x^2+4x+11\right)+7\)
\(=\left(x^2+4x+10\right)^2-7\left(x^2+4x+10\right)-7+7\)
\(=\left(x^2+4x+10\right)\left(x^2+4x+10-7\right)\)
\(=\left(x^2+4x+3\right)\left(x^2+4x+10\right)\)
\(=\left(x+1\right)\left(x+3\right)\left(x^2+4x+10\right)\)
Thực hiện phép tính:
a) 2x. ( x + 1 )
b) ( x + 1 ). ( x + 3 ) – 4
c) ( x + 2 )2 + 3x – 5
Phân tích các đa thức sau thành nhân tử:
a) 3x + 3y
b) x2 – 6x + 9
c) 2x + 2y + 5x + 5y
Tìm x biết:
3x.( x – 1 ) - 5 .( x - 1 ) = 0
\(1,\\ a,=2x^2+2x\\ b,=x^2+4x+3-4=x^2+4x-1\\ c,=x^2+4x+4+3x-5=x^2+7x-1\\ 2,\\ a,=3\left(x+y\right)\\ b,=\left(x-3\right)^2\\ c,=7\left(x+y\right)\\ 3,\\ \Leftrightarrow\left(x-1\right)\left(3x-5\right)=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{5}{3}\end{matrix}\right.\)
Phân tích đa thức thành nhân tử:
a) x^2y + 2xy^2 + xy
b) x^3 + x^2 – 4x – 4
c) x^2 – 2x – 15
d) x^2 – 4 + (x – 2)^2
e) x^2 – y^2 + 2x + 1
g) (x + 9)^2 – 36x^2
h) x^2 – 2xy + y^2 – z^2 + 2zt – t^2
i) x^3 – 3x^2 + 3x – 1 – y^3
\(a,=xy\left(x+2y+1\right)\\ b,=x^2\left(x+1\right)-4\left(x+1\right)=\left(x+1\right)\left(x-2\right)\left(x+2\right)\\ c,=x^2-5x+3x-15=\left(x-5\right)\left(x+3\right)\\ d,=\left(x-2\right)\left(x+2\right)+\left(x-2\right)^2=\left(x-2\right)\left(x+2+x-2\right)=2x\left(x-2\right)\\ e,=\left(x+1\right)^2-y^2=\left(x+y+1\right)\left(x-y+1\right)\\ g,=\left(x+9-6x\right)\left(x+9+6x\right)=\left(9-5x\right)\left(7x+9\right)\\ h,=\left(x-y\right)^2-\left(z-t\right)^2=\left(x-y-z+t\right)\left(x-y+z-t\right)\\ i,=\left(x-1\right)^3-y^3=\left(x-y-1\right)\left(x^2-2x+1+xy+y+y^2\right)\)
c: =(x-5)(x+3)
e: =(x+1-y)(x+1+y)
Phân tích các đa thức sau thành nhân tử:
a) x^3-4x^2+4x
b) x^2-2xy+y^2-9
c)2x^3-x^2-8x+4
d) x^2-y^2-5x+5y
e) 3x^2-6xy+3y^2-12z^2
f) x^3-4x^2+4x-xy^2
g) x^3-2x^2y+xy^2-25x
h) x^3-3x+2
i) 3x^2-7x-10
\(a,=x\left(x-2\right)^2\\ b,=\left(x-y\right)^2-9=\left(x-y-3\right)\left(x-y+3\right)\\ c,=x^2\left(2x-1\right)-4\left(2x-1\right)=\left(x-2\right)\left(x+2\right)\left(2x-1\right)\\ d,=\left(x-y\right)\left(x+y\right)-5\left(x-y\right)=\left(x-y\right)\left(x+y-5\right)\\ e,=3\left[\left(x-y\right)^2-4z^2\right]=3\left(x-y-2z\right)\left(x-y+2z\right)\\ f,=x\left[\left(x-2\right)^2-y^2\right]=x\left(x-y-2\right)\left(x+y-2\right)\\ g,=x\left[\left(x-y\right)^2-25\right]=x\left(x-y-5\right)\left(x-y+5\right)\\ h,=x^3-x-2x+2=x\left(x-1\right)\left(x+1\right)-2\left(x-1\right)\\ =\left(x-1\right)\left(x^2+x-2\right)=\left(x-1\right)^2\left(x+2\right)\\ i,=3x^2+3x-10x-10=\left(x+1\right)\left(3x-10\right)\)
Hãy phân tích các đa thức sau thành nhân tử:
a) 4xy^2 – 2x^2y
b) x^3 + 5x – 4x^2 – 20
c) x^2 (x – y) + 25(y – x)
\(a,=2xy\left(2y-x\right)\\ b,=x^2\left(x-4\right)+5\left(x-4\right)=\left(x^2+5\right)\left(x-4\right)\\ c,=\left(x-y\right)\left(x^2-25\right)=\left(x-y\right)\left(x-5\right)\left(x+5\right)\)