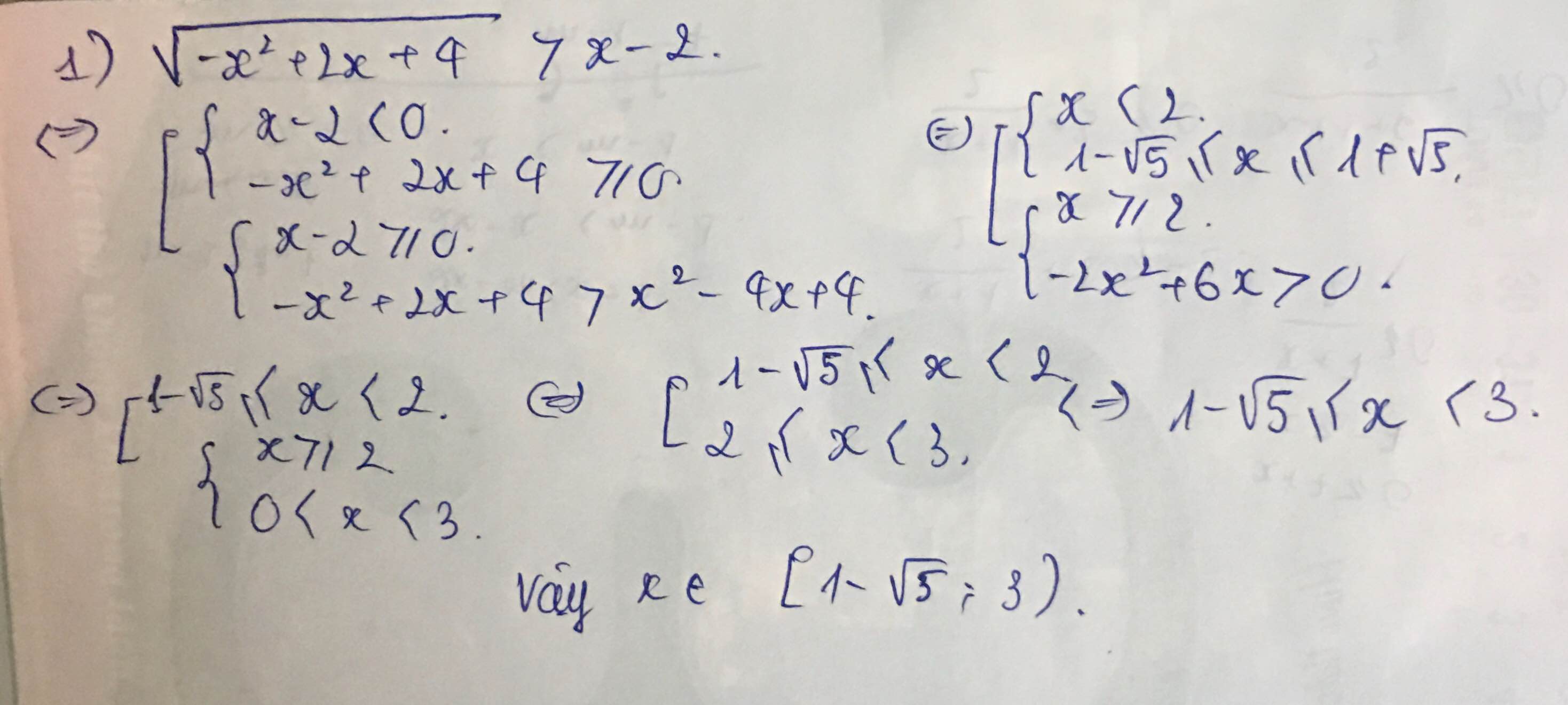Giải giúp mk câu 4 với

Những câu hỏi liên quan
Giải giúp mk 2 bài này với ạ mk đag cần gấp . dịch giúp mk 4 câu của part 7
P6:
1. big
2. been
3. bought
4. people
P7:
1. T
2. F
3. F
4. F
Đúng 1
Bình luận (1)
ai giải giúp mk câu 4 với
Diện tích lớn nhất mà vật đó tiếp xúc với mặt bàn :
\(40.20=800\left(cm^2\right)=0,08\left(m^2\right)\)
Diện tích nhỏ nhất mà vật đó tiếp xúc với mặt bàn :
\(20.20=400\left(cm^2\right)=0,04\left(m^2\right)\)
Áp suất lớn nhất mà vật tác dụng lên mặt bàn :
\(P=\dfrac{F}{S}=\dfrac{3000}{0,04}=75000\left(Pa\right)\)
Áp suất nhỏ nhất mà vật tác dụng lên mặt bàn :
\(P=\dfrac{F}{S}=\dfrac{3000}{0,08}=37500\left(Pa\right)\)
Đúng 1
Bình luận (0)

giúp mk giải chi tiết 4 câu trên ạ
mk cảm ơn
\(5;;\sqrt{\left(x+5\right)\left(3x+4\right)}>4\left(x-1\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}4\left(x-1\right)\le0\\\left(x+5\right)\left(3x+4\right)\ge0\end{matrix}\right.\\\left\{{}\begin{matrix}4\left(x-1\right)\ge0\\\left(x+5\right)\left(3x+4\right)\ge0\\\left(x+5\right)\left(3x+4\right)>16\left(x-1\right)^2\end{matrix}\right.\end{matrix}\right.\)
\(TH:\left\{{}\begin{matrix}4\left(x-1\right)\le0\\\left(x+5\right)\left(3x+4\right)\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\le1\\\left[{}\begin{matrix}x\le-5\\x\ge-\dfrac{4}{3}\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow x\in(-\infty;-5]\cup\left[-\dfrac{4}{3};1\right]\left(1\right)\)
\(TH:\left\{{}\begin{matrix}4\left(x-1\right)\ge0\\\left(x+5\right)\left(3x+4\right)\ge0\\\left(x+5\right)\left(3x+4\right)>16\left(x-1\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge1\\\left[{}\begin{matrix}x\le-5\\x\ge-\dfrac{4}{3}\end{matrix}\right.\\-\dfrac{1}{13}< x< 4\\\end{matrix}\right.\)\(\Rightarrow x\in[1;4)\left(2\right)\)
\(\left(1\right)\left(2\right)\Rightarrow x\in(-\infty;5]\cup[\dfrac{-4}{3};4)\)
Đúng 0
Bình luận (0)
\(6;;;;\sqrt{7x+7}+\sqrt{7x-6}+2\sqrt{49x^2+7x-42}< 181-14x\)
(đoạn 49x^2+7x+42 chắc bạn viết sai đề dấu"-" thành "+")
\(đk:\left\{{}\begin{matrix}7x+7\ge0\\7x-6\ge0\end{matrix}\right.\) \(\Leftrightarrow x\ge\dfrac{6}{7}\)
\(bpt\Leftrightarrow\sqrt{7x+7}+\sqrt{7x-6}+2\sqrt{\left(7x+7\right)\left(7x-6\right)}+14x+1< 182\left(1\right)\)
\(đặt:\sqrt{7x+7}+\sqrt{7x-6}=t>0\)
\(\Rightarrow t^2=14x+1+2\sqrt{\left(7x+7\right)\left(7x-6\right)}\)
\(\Rightarrow\left(1\right)\Leftrightarrow t^2+t< 182\Leftrightarrow-14< t< 13\)
\(\Rightarrow\sqrt{7x+7}+\sqrt{7x-6}< 13\Leftrightarrow14x+1+2\sqrt{\left(7x+7\right)\left(7x-6\right)}< 169\)
\(\Leftrightarrow2\sqrt{\left(7x+7\right)\left(7x-6\right)}< 168-14x\)
\(\Leftrightarrow\left\{{}\begin{matrix}168-14x\ge0\\\left(7x+7\right)\left(7x-6\right)\ge0\\4\left(7x+7\right)\left(7x-6\right)< \left(168-14x\right)^2\\\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le12\\\left[{}\begin{matrix}x\le-1\\x\ge\dfrac{6}{7}\end{matrix}\right.\\x< 6\\\end{matrix}\right.\)\(\Rightarrow\dfrac{6}{7}\le x< 6\)
Đúng 0
Bình luận (0)
\(7;\) \(3\sqrt{x}+\dfrac{3}{2\sqrt{x}}< 2x+\dfrac{1}{2x}-1\left(đk:x>0\right)\)
\(\Leftrightarrow3\left(\sqrt{x}+\dfrac{1}{2\sqrt{x}}\right)< 2\left(x+\dfrac{1}{4x}\right)-1\left(1\right)\)
\(đặt:\sqrt{x}+\dfrac{1}{2\sqrt{x}}=t>0\)
\(\Leftrightarrow t^2=\sqrt{x}^2+2.\sqrt{x}.\dfrac{1}{2\sqrt{x}}+\left(\dfrac{1}{2\sqrt{x}}\right)^2=x+\dfrac{1}{4x}+1\)
\(\Rightarrow x+\dfrac{1}{4x}=t^2-1\)
\(\left(1\right)\Leftrightarrow3t< 2\left(t^2-1\right)-1\)
\(\Leftrightarrow2t^2-3t-3>0\Leftrightarrow\left[{}\begin{matrix}t< \dfrac{3-\sqrt{33}}{4}\\t>\dfrac{3+\sqrt{33}}{4}\end{matrix}\right.\)
\(\Rightarrow\sqrt{x}+\dfrac{1}{2\sqrt{x}}>\dfrac{3+\sqrt{33}}{4}\)
\(\Leftrightarrow\dfrac{2x+1}{2\sqrt{x}}>\dfrac{3+\sqrt{33}}{4}\)
\(\Leftrightarrow\sqrt{x}< \dfrac{2\left(2x+1\right)}{3+\sqrt{33}}\Leftrightarrow\left\{{}\begin{matrix}x>0\\2\left(2x+1\right)\ge0\\x< \left[\dfrac{2\left(2x+1\right)}{3+\sqrt{33}}\right]^2\\\end{matrix}\right.\)
đến đây dễ dàng rồi như mấy ý trên bạn tự giải quyết để tìm ra x
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Mn giải giúp mk câu 4 ạ
Câu 4:
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Vậy: BC=10cm
Đúng 1
Bình luận (0)
a) Xét ΔABC có BD là đường phân giác ứng với cạnh AC(gt)
nên \(\dfrac{DA}{DC}=\dfrac{BA}{BC}\)(Tính chất tia phân giác của tam giác)
hay \(\dfrac{DA}{DC}=\dfrac{6}{10}=\dfrac{3}{5}\)
Đúng 1
Bình luận (0)
b) Xét ΔABD vuông tại A và ΔEBC vuông tại E có
\(\widehat{ABD}=\widehat{EBC}\)(BD là tia phân giác của \(\widehat{ABC}\))
Do đó: ΔABD\(\sim\)ΔEBC(g-g)
Đúng 1
Bình luận (0)
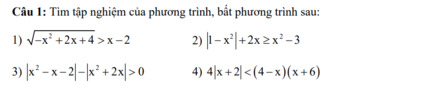
giải chi tiết 4 câu này giúp mk vs
mk cảm ơn <3
Giúp mk giải bài 2 câu 1 với mk đang cần gấp 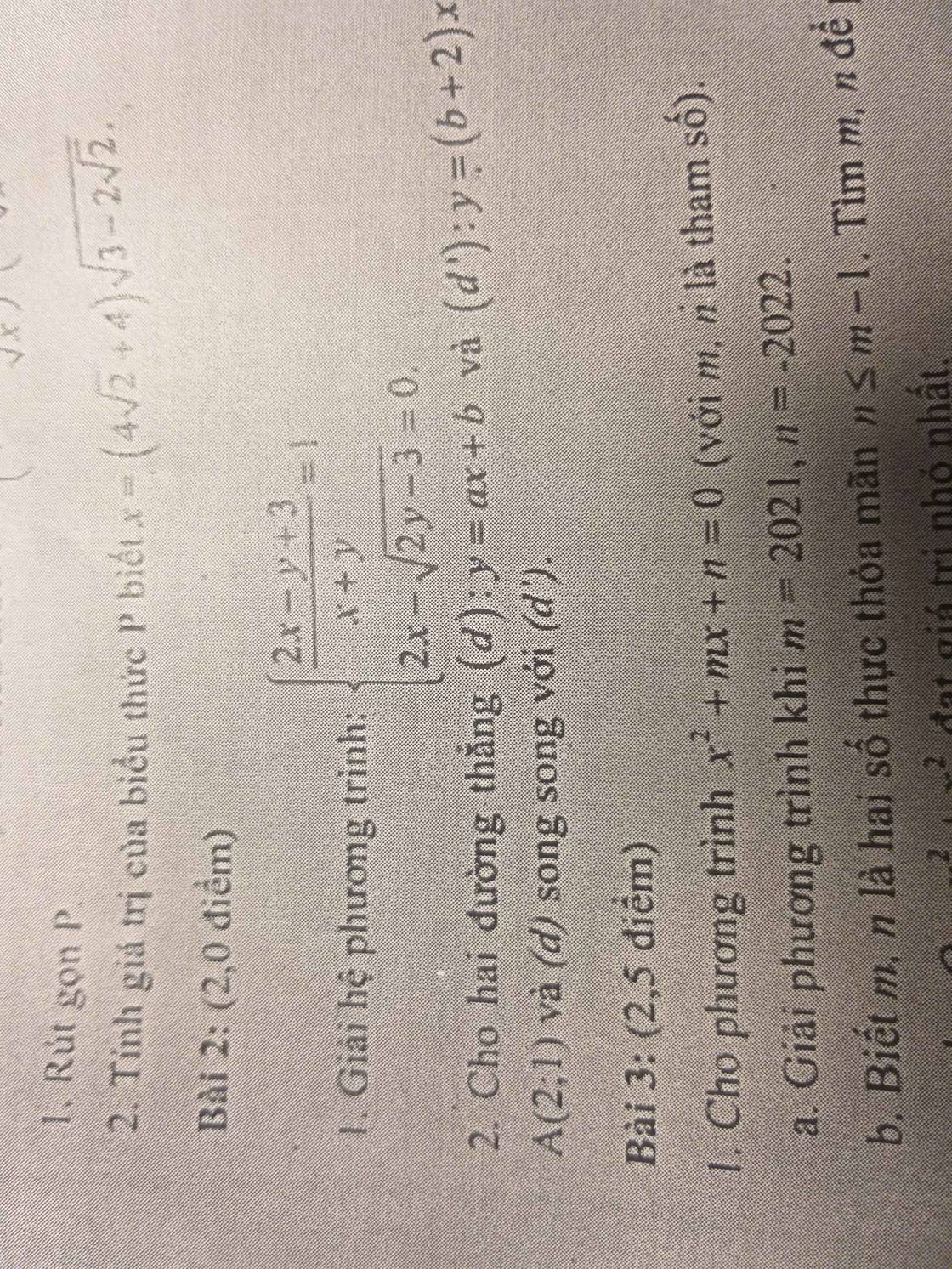
ĐK: \(\left\{{}\begin{matrix}x\ne-y\\y\ge\dfrac{3}{2}\end{matrix}\right.\).
\(\left\{{}\begin{matrix}\dfrac{2x-y+3}{x+y}=1\\2x-\sqrt{2y-3}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2x-y+3}{x+y}-1=0\\2x-\sqrt{2y-3}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2x-y+3}{x+y}-\dfrac{x+y}{x+y}=0\\2x-\sqrt{2y-3}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x-y+3-x-y=0\\2x-\sqrt{2y-3}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-2y+3=0\\2x-\sqrt{2y-3}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-\left(2y-3\right)=0\\2x-\sqrt{2y-3}=0\end{matrix}\right..\)
Đặt a = x, b = \(\sqrt{2y-3}\).
Hệ phương trình trở thành: \(\left\{{}\begin{matrix}a-b^2=0\\2a-b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=b^2\\2b^2-b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=b^2\\b\left(2b-1\right)=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=b^2\\\left[{}\begin{matrix}b=0\\b=\dfrac{1}{2}\end{matrix}\right.\end{matrix}\right.\left\{{}\begin{matrix}\left[{}\begin{matrix}a=0\\a=\dfrac{1}{4}\end{matrix}\right.\\\left[{}\begin{matrix}b=0\\b=\dfrac{1}{2}\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x=0\\x=\dfrac{1}{4}\end{matrix}\right.\\\left[{}\begin{matrix}y=\dfrac{3}{2}\\2y-3=\dfrac{1}{4}\end{matrix}\right.\end{matrix}\right.\left\{{}\begin{matrix}\left[{}\begin{matrix}x=0\\x=\dfrac{1}{4}\end{matrix}\right.\\\left[{}\begin{matrix}y=\dfrac{3}{2}\\2y=\dfrac{13}{4}\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x=0\\x=\dfrac{1}{4}\end{matrix}\right.\\\left[{}\begin{matrix}y=\dfrac{3}{2}\\y=\dfrac{13}{8}\end{matrix}\right.\end{matrix}\right..\)
Vậy hệ phương trình có nghiệm (x;y) \(\in\) \(\left\{\left(0;\dfrac{3}{2}\right),\left(\dfrac{1}{4};\dfrac{13}{8}\right)\right\}\).
Đúng 0
Bình luận (0)
Giải giúp mk câu 4 vs ạ. Thanks
THAM KHẢO
+ Giống nhau: Sự bay hơi và sự sôi giống nhau là đều là sự chuyển từ thể lỏng sang thể hơi.
+ Khác nhau: Sự bay hơi diễn ra trên bề mặt chất lỏng ở mọi nhiệt độ, còn sự sôi là sự bay hơi cả trên mặt và trong lòng chất lỏng, diễn ra ở nhiệt độ sôi.
Đúng 2
Bình luận (0)
 Mọi người giúp mk giải chi tiết câu này với ạ. Mk cảm ơn
Mọi người giúp mk giải chi tiết câu này với ạ. Mk cảm ơn
\(I=\int\dfrac{2}{2+5sinxcosx}dx=\int\dfrac{2sec^2x}{2sec^2x+5tanx}dx\\ =\int\dfrac{2sec^2x}{2tan^2x+5tanx+2}dx\)
We substitute :
\(u=tanx,du=sec^2xdx\\ I=\int\dfrac{2}{2u^2+5u+2}du\\ =\int\dfrac{2}{2\left(u+\dfrac{5}{4}\right)^2-\dfrac{9}{8}}du\\ =\int\dfrac{1}{\left(u+\dfrac{5}{4}\right)^2-\dfrac{9}{16}}du\\ \)
Then,
\(t=u+\dfrac{5}{4}\\I=\int\dfrac{1}{t^2-\dfrac{9}{16}}dt\\ =\int\dfrac{\dfrac{2}{3}}{t-\dfrac{3}{4}}-\dfrac{\dfrac{2}{3}}{t+\dfrac{3}{4}}dt\)
Finally,
\(I=\dfrac{2}{3}ln\left(\left|\dfrac{t-\dfrac{3}{4}}{t+\dfrac{3}{4}}\right|\right)+C=\dfrac{2}{3}ln\left(\left|\dfrac{tanx+\dfrac{1}{2}}{tanx+2}\right|\right)+C\)
Đúng 1
Bình luận (0)
Giúp mk với câu 25 giải PT ạ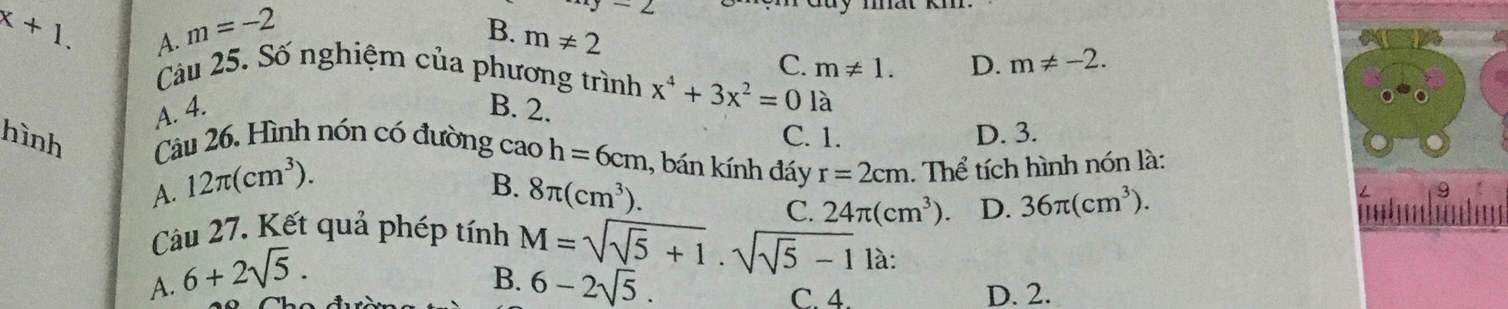
\(x^4+3x^2=0\)
Có \(x^4\ge0;\forall x\); \(3x^2\ge0;\forall x\)
=> VT\(\ge0;\forall x\)
Dấu = xảy ra <=> x=0
Ý C
Đúng 1
Bình luận (0)