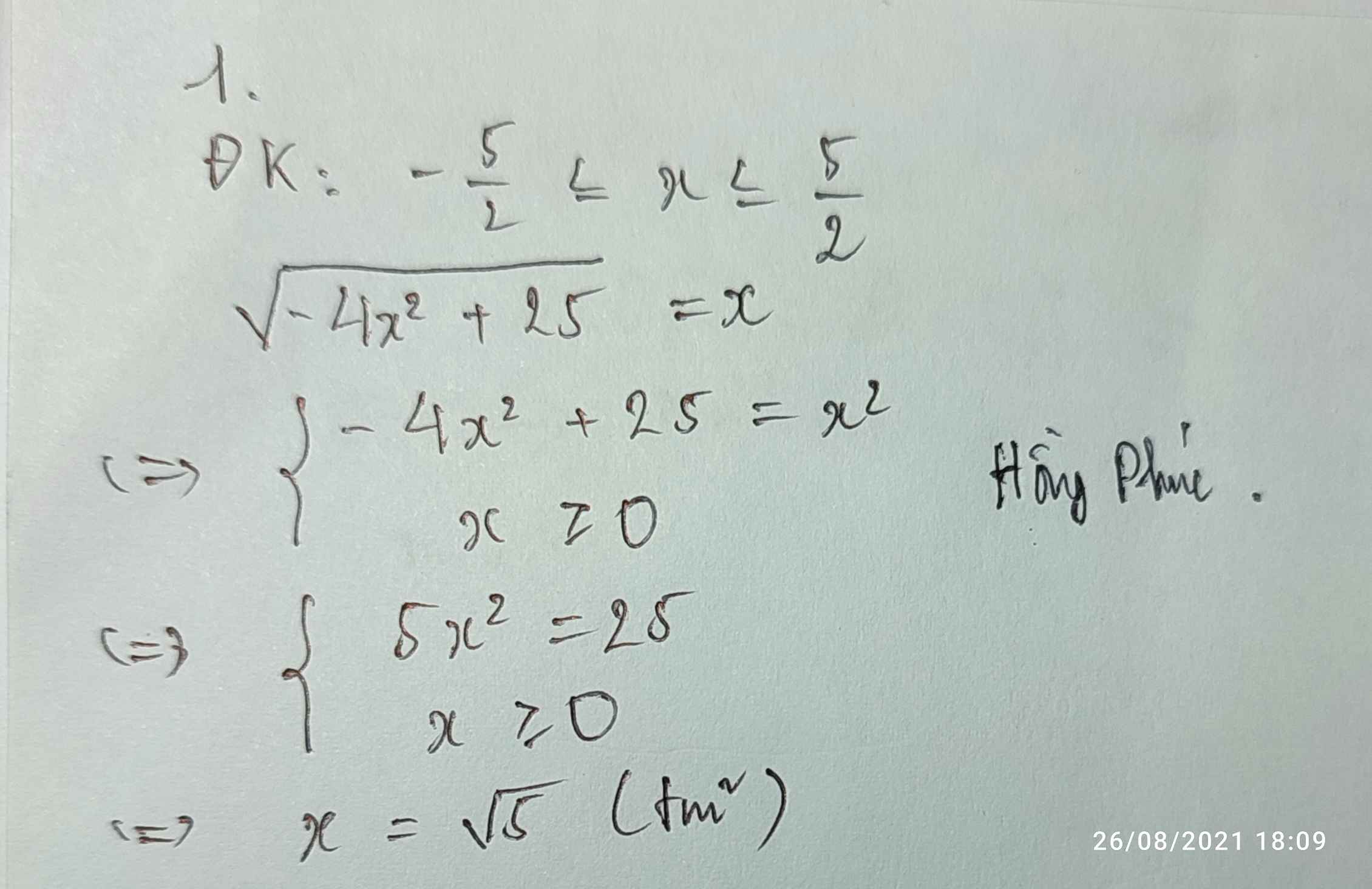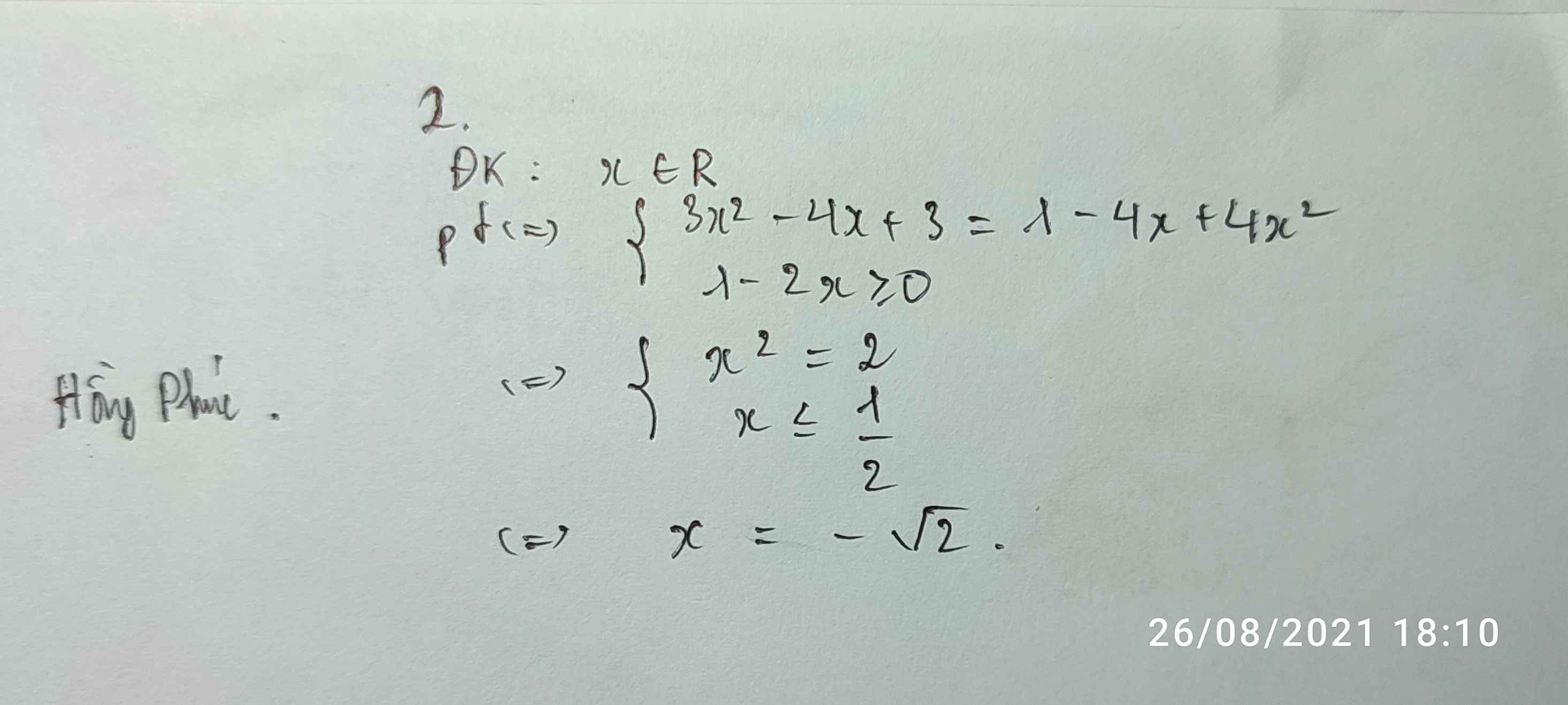a: \(x^2-2-x+\sqrt{2}=0\)

=>\(\left(x-\sqrt{2}\right)\left(x+\sqrt{2}\right)-\left(x-\sqrt{2}\right)=0\)

=>\(\left(x-\sqrt{2}\right)\left(x+\sqrt{2}-1\right)=0\)

=>\(\left[{}\begin{matrix}x=\sqrt{2}\\x=-\sqrt{2}+1\end{matrix}\right.\)

b: \(\left(1-\sqrt{2}\right)x^2-2\left(1+\sqrt{2}\right)x+1+3\sqrt{2}=0\)

\(\Delta=\left(-2-2\sqrt{2}\right)^2-4\left(1-\sqrt{2}\right)\left(1+3\sqrt{2}\right)\)

\(=12+8\sqrt{2}+4\left(\sqrt{2}-1\right)\left(3\sqrt{2}+1\right)\)

\(=12+8\sqrt{2}+4\left(6+\sqrt{2}-3\sqrt{2}-1\right)\)

\(=12+8\sqrt{2}+24-8\sqrt{2}-4=32>0\)

Do đó: Phương trình có hai nghiệm phân biệt là:

\(\left\{{}\begin{matrix}x_1=\dfrac{2\left(1+\sqrt{2}\right)-4\sqrt{2}}{2\left(1-\sqrt{2}\right)}=1\\x_2=\dfrac{2\left(1+\sqrt{2}\right)+4\sqrt{2}}{2\left(1-\sqrt{2}\right)}=-7-4\sqrt{2}\end{matrix}\right.\)

a: ĐKXĐ: x>=1

\(\dfrac{1}{2}\sqrt{x-1}-\sqrt{4x-4}+3=0\)

=>\(3+\dfrac{1}{2}\sqrt{x-1}-2\sqrt{x-1}=0\)

=>\(3-\dfrac{3}{2}\sqrt{x-1}=0\)

=>\(\dfrac{3}{2}\sqrt{x-1}=3\)

=>\(\sqrt{x-1}=2\)

=>x-1=4

=>x=5(nhận)

b: \(\sqrt{x^2-4x+4}+x-2=0\)

=>\(\sqrt{\left(x-2\right)^2}=-x+2\)

=>|x-2|=-(x-2)

=>x-2<=0

=>x<=2

c: 

ĐKXĐ: 7-x>=0

=>x<=7

\(\sqrt{7-x}+1=x\)

=>\(\sqrt{7-x}=x-1\)

=>\(\left\{{}\begin{matrix}x-1>=0\\7-x=x^2-2x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}1< =x< =7\\x^2-2x+1-7+x=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}1< =x< =7\\x^2-x-6=0\end{matrix}\right.\Leftrightarrow x=3\)

a.

$x^2-11=0$

$\Leftrightarrow x^2=11$

$\Leftrightarrow x=\pm \sqrt{11}$

b. $x^2-12x+52=0$

$\Leftrightarrow (x^2-12x+36)+16=0$

$\Leftrightarrow (x-6)^2=-16< 0$ (vô lý)

Vậy pt vô nghiệm.

c.

$x^2-3x-28=0$

$\Leftrightarrow x^2+4x-7x-28=0$

$\Leftrightarrow x(x+4)-7(x+4)=0$

$\Leftrightarrow (x+4)(x-7)=0$

$\Leftrightarrow x+4=0$ hoặc $x-7=0$

$\Leftrightarrow x=-4$ hoặc $x=7$

d.

$x^2-11x+38=0$

$\Leftrightarrow (x^2-11x+5,5^2)+7,75=0$

$\Leftrightarrow (x-5,5)^2=-7,75< 0$ (vô lý)

Vậy pt vô nghiệm

e.

$6x^2+71x+175=0$

$\Leftrightarrow 6x^2+21x+50x+175=0$

$\Leftrightarrow 3x(2x+7)+25(2x+7)=0$

$\Leftrightarrow (3x+25)(2x+7)=0$

$\Leftrightarrow 3x+25=0$ hoặc $2x+7=0$

$\Leftrightarrow x=-\frac{25}{3}$ hoặc $x=-\frac{7}{2}$

f.

$x^2-(\sqrt{2}+\sqrt{8})x+4=0$

$\Leftrightarrow x^2-\sqrt{2}x-2\sqrt{2}x+4=0$

$\Leftrightarrow x(x-\sqrt{2})-2\sqrt{2}(x-\sqrt{2})=0$

$\Leftrightarrow (x-\sqrt{2})(x-2\sqrt{2})=0$

$\Leftrightarrow x-\sqrt{2}=0$ hoặc $x-2\sqrt{2}=0$

$\Leftrightarrow x=\sqrt{2}$ hoặc $x=2\sqrt{2}$

g.

$(1+\sqrt{3})x^2-(2\sqrt{3}+1)x+\sqrt{3}=0$

$\Leftrightarrow (1+\sqrt{3})x^2-(1+\sqrt{3})x-(\sqrt{3}x-\sqrt{3})=0$

$\Leftrightarrow (1+\sqrt{3})x(x-1)-\sqrt{3}(x-1)=0$

$\Leftrightarrow (x-1)[(1+\sqrt{3})x-\sqrt{3}]=0$

$\Leftrightarrow x-1=0$ hoặc $(1+\sqrt{3})x-\sqrt{3}=0$

$\Leftrightarrow x=1$ hoặc $x=\frac{3-\sqrt{3}}{2}$

a: \(\Leftrightarrow\sqrt{x-2}\left(1-3\sqrt{x+2}\right)=0\)

=>x-2=0 hoặc x+2=1/9

=>x=-17/9(loại) hoặc x=2

b: \(\Leftrightarrow\sqrt{x^2-1}\left(1-\sqrt{x^2-1}\right)=0\)

=>x^2-1=0 hoặc x^2-1=1

=>x^2=1 hoặc x^2=2

=>\(x\in\left\{1;-1;\sqrt{2};-\sqrt{2}\right\}\)

a) \(P=\left(\dfrac{x+2}{x\sqrt{x}-1}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}+\dfrac{1}{1-\sqrt{x}}\right):\dfrac{\sqrt{x}-1}{2}\)

\(P=\left(\dfrac{x+2}{\left(\sqrt{x}\right)^3-1^3}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}+\dfrac{1}{1-\sqrt{x}}\right)\cdot\dfrac{2}{\sqrt{x}-1}\)

\(P=\left(\dfrac{x+2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}+\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}-\dfrac{x+\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\right)\cdot\dfrac{2}{\sqrt{x}-1}\)\(P=\left(\dfrac{x+2+x-\sqrt{x}-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\right)\cdot\dfrac{2}{\sqrt{x}-1}\)

\(P=\dfrac{x-2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\dfrac{2}{\sqrt{x}-1}\)

\(P=\dfrac{\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\dfrac{2}{\sqrt{x}-1}\)

\(P=\dfrac{2\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)^2\left(x+\sqrt{x}+1\right)}\)

\(P=\dfrac{2}{x+\sqrt{x}+1}\)

b) Mà với \(x\ge0\) và \(x\ne1\) thì 

\(x+\sqrt{x}+1\ge0\) và \(2>0\) nên \(P>0\)

a: \(P=\dfrac{x+2+x-\sqrt{x}-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\dfrac{2}{\sqrt{x}-1}\)

\(=\dfrac{2}{x+\sqrt{x}+1}\cdot\dfrac{\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)^2}=\dfrac{2}{x+\sqrt{x}+1}\)

b: x+căn x+1+1>=1>0

2>0

=>P>0 với mọi x thỏa mãn x>=0 và x<>1

a.

\(\Leftrightarrow\dfrac{x-\sqrt{1+x^2}+x+\sqrt{1+x^2}}{\left(x-\sqrt{1+x^2}\right)\left(x+\sqrt{1+x^2}\right)}+2=0\)

\(\Leftrightarrow\dfrac{2x}{x^2-1-x^2}+2=0\)

\(\Leftrightarrow-2x+2=0\)

\(\Leftrightarrow x=1\)

b.

ĐKXĐ: \(x\ge a\)

Đặt \(\sqrt{x-a}=t\ge0\Rightarrow x=t^2+a\)

Pt trở thành:

\(2\left(t^2+a\right)-5at+2a^2-2a=0\)

\(\Leftrightarrow2t^2-5at+2a^2=0\)

\(\Leftrightarrow\left(2t-a\right)\left(t-2a\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}t=\dfrac{a}{2}\\t=2a\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x-a}=\dfrac{a}{2}\\\sqrt{x-a}=2a\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{a^2}{4}+a\\x=4a^2+a\end{matrix}\right.\)