giúp e câu b ạ tìm đkxđ

Những câu hỏi liên quan
mọi người chỉ cần lm câu a và c giúp e thôi ạ có cả đkxđ ạ vd:x>3,... em CẢM ƠN NHIỀU Ạ
a)\(đkx\ge1,x\ne-1\)
\(\sqrt{\dfrac{x-1}{x+1}}=2\)
\(\Leftrightarrow\dfrac{x-1}{x+1}=4\)
\(\Leftrightarrow x-1=4x-4\)
\(\Leftrightarrow x=1\)(nhận)
Vậy S=\(\left\{1\right\}\)
c)đk\(25x^2-10x+1=\) \(\left(5x-1\right)^2\ge0\Leftrightarrow x\ge\dfrac{1}{5}\)
\(\sqrt{25x^2-10x+1}+2x=1\)
\(\Leftrightarrow\sqrt{\left(5x-1\right)^2}+2x=1\)
\(\Leftrightarrow5x-1+2x=1\)
\(\Leftrightarrow x=\dfrac{2}{7}\)(nhận)
Vậy S=\(\left\{\dfrac{2}{7}\right\}\)
Đúng 1
Bình luận (0)
c: Ta có: \(\sqrt{25x^2-10x+1}+2x=1\)
\(\Leftrightarrow\left|5x-1\right|=1-2x\)
\(\Leftrightarrow\left[{}\begin{matrix}5x-1=1-2x\left(x\ge\dfrac{1}{5}\right)\\5x-1=2x-1\left(x< \dfrac{1}{5}\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2}{7}\left(nhận\right)\\x=0\left(nhận\right)\end{matrix}\right.\)
Đúng 1
Bình luận (0)
giúp em giải câu d bài 3 với ạ (nhớ tìm ĐKXĐ)

ĐIều kiện:`x^2-7x+8>=0`
`<=>x^2-2*x*7/2+49/4-17/4>=0`
`<=>(x-7/2)^2-17/4>=0`
`<=>(x-7/2)^2>=17/4`
`<=>|x-7/2|>=sqrt{17}/2`
`<=>` \(\left[ \begin{array}{l}x \ge \dfrac{7+\sqrt{17}}{2}\\x \le \dfrac{-\sqrt{17}+7}{2}\end{array} \right.\)
`pt<=>x^2-7x+sqrt{x^2-7x+8}-12=0`
`<=>x^2-7x+8+sqrt{x^2-7x+8}-20=0`
Đặt `a=sqrt{x^2-7x+8}(a>=0)`
`pt<=>a^2+a-20=0`
`<=>a=4(tm),a=-5(l)`
`<=>x^2-7x+8=16`
`<=>x^2-7x-8=0`
`a-b+c=0`
`=>x_1=-1(tm),x_2=8(tm)`
Vậy `S={-1,8}`
Đúng 2
Bình luận (0)
giúp iem với, tìm đkxđ vs ạ, thanks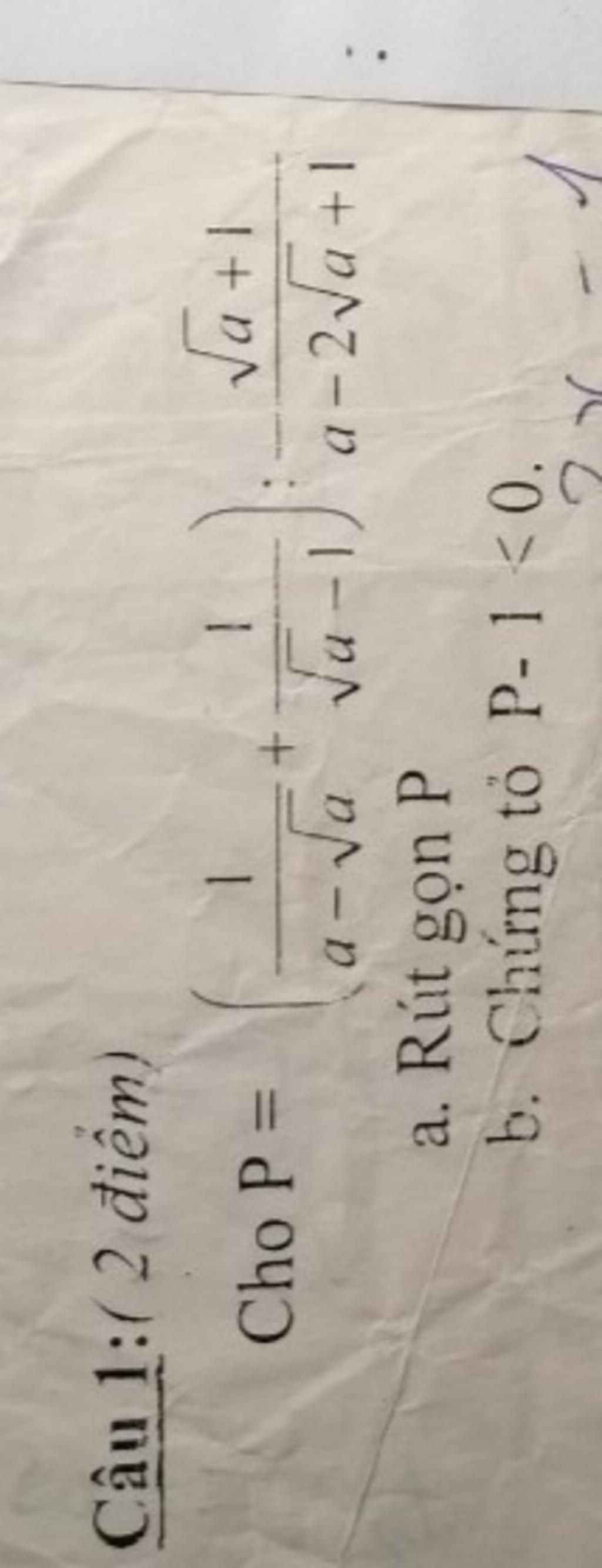
a: \(P=\dfrac{\sqrt{a}+1}{\sqrt{a}\left(\sqrt{a}-1\right)}\cdot\dfrac{\left(\sqrt{a}-1\right)^2}{\sqrt{a}+1}=\dfrac{\sqrt{a}-1}{\sqrt{a}}\)
b: \(P-1=\dfrac{\sqrt{a}-1-\sqrt{a}}{\sqrt{a}}=\dfrac{-1}{\sqrt{a}}< 0\)
Đúng 0
Bình luận (0)
Tìm đkxđ  giải giúp mình câu 19,21,23,24,18,10,13 với
giải giúp mình câu 19,21,23,24,18,10,13 với
\(19,ĐKXĐ:\dfrac{-2\sqrt{6}+\sqrt{23}}{-x+5}\ge0;x\ne5\\ \Leftrightarrow5-x< 0\left(-2\sqrt{6}+\sqrt{23}< 0\right)\\ \Leftrightarrow x>5\)
\(21,ĐKXĐ:x\ne7;\dfrac{2\sqrt{15}-\sqrt{59}}{x-7}\ge0\\ \Leftrightarrow x-7>0\left(2\sqrt{15}-\sqrt{59}>0\right)\\ \Leftrightarrow x>7\)
\(23,ĐKXĐ:49x^2-24x+4\ge0\Leftrightarrow\left(49x^2-14\cdot\dfrac{12}{7}x+\dfrac{144}{49}\right)+\dfrac{52}{49}\ge0\\ \Leftrightarrow\left(7x-\dfrac{12}{7}\right)^2+\dfrac{52}{49}\ge0\\ \Leftrightarrow x\in R\)
Đúng 2
Bình luận (0)
Mọi người giúp em tìm đkxđ của hệ phương trình với ạ. Em cảm ơn
cho bthuc: Q=\((\dfrac{\sqrt{x}}{\sqrt{x}-1}+\dfrac{\sqrt{x}}{x-1}):(\dfrac{2}{x}-\dfrac{2-x}{x\sqrt{x}+x})\)
a) Nêu ĐKXĐ và rút gọn Q
b) Tìm x để Q>2
c) Tìm GTNN của \(\sqrt{x}\)
nhờ mn giải hộ giúp e ạ
a: ĐKXĐ: x>0; x<>1
\(Q=\dfrac{x+\sqrt{x}+\sqrt{x}}{x-1}:\dfrac{2\left(\sqrt{x}+1\right)-2+x}{x\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)}{x-1}\cdot\dfrac{x\left(\sqrt{x}+1\right)}{2\sqrt{x}+x}\)
\(=\dfrac{x}{\sqrt{x}-1}\)
b: Q>2
=>Q-2>0
=>\(\dfrac{x-\sqrt{x}+1}{\sqrt{x}-1}>0\)
=>căn x-1>0
=>x>1
Đúng 1
Bình luận (0)
a) ĐK: \(\left\{{}\begin{matrix}x\ge0\\x\ne1\end{matrix}\right.\)
\(Q=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}+\dfrac{\sqrt{x}}{x-1}\right):\left(\dfrac{2}{x}-\dfrac{2-x}{x\sqrt{x}+x}\right)\)
\(=\left(\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}+\dfrac{\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right):\left(\dfrac{2\left(\sqrt{x}+1\right)}{x\left(\sqrt{x}+1\right)}-\dfrac{2-x}{x\left(\sqrt{x}+1\right)}\right)\)
\(=\dfrac{x+\sqrt{x}+\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}:\dfrac{2\sqrt{x}+2-2+x}{x\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x+2\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}.\dfrac{x\left(\sqrt{x}+1\right)}{x+2\sqrt{x}}\)
\(=\dfrac{x}{\sqrt{x}-1}\)
b) Q>2 <=> \(\dfrac{x}{\sqrt{x}-1}>2\Leftrightarrow x>2\sqrt{x}-2\)
\(\Leftrightarrow x-2\sqrt{x}+2>0\)
\(\Leftrightarrow\left(\sqrt{x}-1\right)^2+1>0\)
\(\Leftrightarrow\left(\sqrt{x}-1\right)^2\ge0\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}-1\le0\\\sqrt{x}-1\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x\ge1\\x\le1\end{matrix}\right.\)
KL:.....
Đúng 0
Bình luận (0)
cho N = \(\left(\frac{2}{x^2+x}+\frac{1}{x+1}\right):\frac{1}{x+1}\)
a. tìm ĐKXĐ
b. rút gọn N
c. tìm x thuộc z để N nhận gtri nguyên
d.tìm x để N<1
giúp e với ạ <3
a + b , \(N=\left(\frac{2}{x^2+x}+\frac{1}{x+1}\right):\frac{1}{x+1}\)ĐK : \(x\ne0;-1\)
\(=\left(\frac{2}{x\left(x+1\right)}+\frac{x}{x\left(x+1\right)}\right):\frac{1}{x+1}=\frac{x+2}{x\left(x+1\right)}.\frac{x+1}{1}=\frac{x+2}{x}\)
c, Ta có : \(\frac{x+2}{x}=1+\frac{2}{x}\)
Để N nguyên khi \(2⋮x\Rightarrow x\inƯ\left(2\right)=\left\{\pm1;\pm2\right\}\)
Vậy \(x=\pm1;\pm2\)thì N nguyên
d, ta có : \(N< 1\Rightarrow\frac{x+2}{x}< 1\Leftrightarrow\frac{x+2-x}{x}< 0\Rightarrow x< 0\)vì 2 > 0
bổ sung hộ mình
c, Kết hợp với đk vậy \(x=1;\pm2\)thì N nguyên
d, Kết hợp với đk vậy \(x< 0;x\ne-1\)
a) đk: \(\hept{\begin{cases}x\ne0\\x\ne-1\end{cases}}\)
b) \(N=\left(\frac{2}{x^2+x}+\frac{1}{x+1}\right)\div\frac{1}{x+1}\)
\(N=\frac{2+x}{x\left(x+1\right)}\cdot\left(x+1\right)=\frac{2+x}{x}\)
c) \(N=\frac{2+x}{x}=\frac{2}{x}+1\)
Để N nguyên \(x\inƯ\left(2\right)\Rightarrow x\in\left\{1;-2;2\right\}\)
d) \(N< 1\Leftrightarrow\frac{2}{x}+1< 1\Rightarrow\frac{2}{x}< 0\Rightarrow x< 0\)
Tìm ĐKXĐ và rút gọn A:
\(A=\sqrt{x+4\sqrt{x-4}}+\sqrt{x-4\sqrt{x-4}}\)
Giúp em với ạ. Em cảm ơn ạ.
Đk: \(x\ge4\)
\(A=\sqrt{x+4\sqrt{x-4}}+\sqrt{x-4\sqrt{x-4}}\)
\(=\sqrt{\left(x-4\right)+4\sqrt{x-4}+4}+\sqrt{\left(x-4\right)-4\sqrt{x-4}+4}\)
\(=\sqrt{\left(\sqrt{x-4}+2\right)^2}+\sqrt{\left(\sqrt{x-4}-2\right)^2}\)
\(=\sqrt{x-4}+2+\left|\sqrt{x-4}-2\right|\)
TH1:\(\sqrt{x-4}>2\Leftrightarrow x>8\)
\(A=\sqrt{x-4}+2+\sqrt{x-4}-2=2\sqrt{x-4}\)
TH2:\(\sqrt{x-4}\le2\Leftrightarrow4\le x\le8\)
\(A=\sqrt{x-4}+2-\left(\sqrt{x-4}-2\right)=4\)
Vậy...
Đúng 0
Bình luận (0)
giúp mình bài này vs ạ
bài 1:so sánh các căn sau
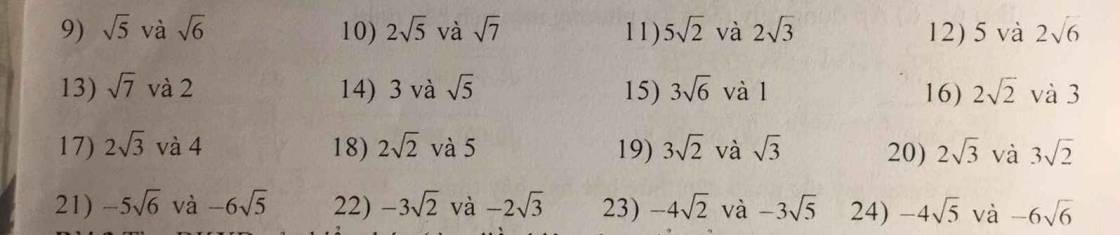
bài 2 :tìm ĐKXĐ của biểu thức (tìm đk của x để biểu thức sau có nghĩa)
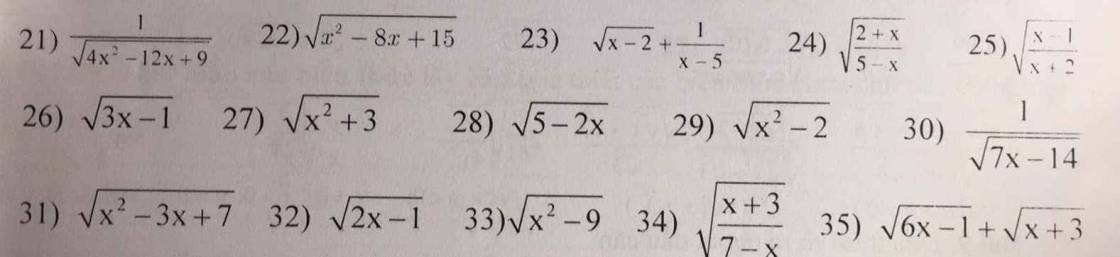
Bài 1
Mình làm mẫu một số câu thôi nhé
\(9,\sqrt{5}=\left(\sqrt{5}\right)^2=5\\ \sqrt{6}=\left(\sqrt{6}\right)^2=6\)
Vì \(5< 6\)
\(\Rightarrow\sqrt{5}< \sqrt{6}\)
\(10,2\sqrt{5}=\left(2\sqrt{5}\right)^2=20\\ \sqrt{7}=\left(\sqrt{7}\right)^2=7\)
Vì \(20>7\)
\(\Rightarrow2\sqrt{5}>\sqrt{7}\)
\(11,5\sqrt{2}=\left(5\sqrt{2}\right)^2=50\\ 2\sqrt{3}=\left(2\sqrt{3}\right)^2=12\)
Vì \(50>12\Rightarrow5\sqrt{2}>2\sqrt{3}\)
\(12,2\sqrt{6}=\left(2\sqrt{6}\right)^2=24\\ 5=5^2=25\)
Vì \(25>24\Rightarrow5>2\sqrt{6}\)
\(13,\sqrt{7}=\left(\sqrt{7}\right)^2=7\\ 2=2^2=4\)
Vì \(7>4\Rightarrow\sqrt{7}>2\)
\(14,3=3^2=9\\ \sqrt{5}=\left(\sqrt{5}\right)^2=5\)
Vì \(9>5\Rightarrow3>\sqrt{5}\)
\(15,3\sqrt{6}=\left(3\sqrt{6}\right)^2=54\)
Vì \(54>1\Rightarrow3\sqrt{6}>1\)
\(16,2\sqrt{2}=\left(2\sqrt{2}\right)^2=8\\ 3=3^2=9\)
Vì \(8< 9\Rightarrow2\sqrt{2}< 3\)
Phương pháp làm dạng bài này là bình phương hai vế rồi so sánh
Đúng 2
Bình luận (0)
Bài 2
Gợi ý : Biểu thức dưới dấu căn \(\ge\) 0
Lưu ý : Nếu biểu thức dưới dấu căn ở dưới mẫu thì \(>0\)
\(21,ĐK:4x^2-12x+9>0\\ \Rightarrow\left(2x-3\right)^2>0\\ \Leftrightarrow x\ne\dfrac{3}{2}\)
\(22,ĐK:x^2-8x+15\ge0\\ \Rightarrow\left[{}\begin{matrix}x\le3\\x\ge5\end{matrix}\right.\)
\(23,ĐK:\left\{{}\begin{matrix}x-2\ge0\\x-5\ne0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x\ge2\\x\ne5\end{matrix}\right.\)
\(24,ĐK:\left\{{}\begin{matrix}\dfrac{2+x}{5-x}\ge0\\5-x\ne0\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}2+x\ge0\\5-x\ge0\\x\ne5\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x\ge-2\\x\le5\\x\ne5\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x\ge-2\\x< 5\end{matrix}\right.\left(t/m\right)\)
Hoặc
\(\left\{{}\begin{matrix}2+x\le0\\5-x\le0\\5-x\ne0\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x\le-2\\x\ge5\\x\ne5\end{matrix}\right.\left(loại\right)\)
Đúng 2
Bình luận (0)
Chỉ đăng tối đa 10 - 15 câu hỏi thôi, câu trước GV nhắc bạn rồi mà giờ bạn vẫn còn đăng nữa thì nên bị xóa câu hỏi.
Đúng 1
Bình luận (3)
Xem thêm câu trả lời




























