Giải hệ phương trình
x+y+|x|=25
x-y+|y|=30
Những câu hỏi liên quan
Giải các hệ phương trình sau bằng phương pháp thế:
a
)
x
−
y
3
3
x
−
4
y...
Đọc tiếp
Giải các hệ phương trình sau bằng phương pháp thế:
a ) x − y = 3 3 x − 4 y = 2 b ) 7 x − 3 y = 5 4 x + y = 2 c ) x + 3 y = − 2 5 x − 4 y = 11
Cách 1
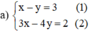
Từ (1) rút ra được y = x – 3
Thế vào phương trình (2) ta được:
3x – 4.(x – 3) = 2 ⇔ 3x – 4x + 12 = 2 ⇔ x = 10
Từ x = 10 ⇒ y = x – 3 = 7.
Vậy hệ phương trình có nghiệm duy nhất (10 ; 7).
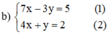
Từ (2) rút ra được y = -4x + 2.
Thế y = -4x + 2 vào phương trình (1) ta được :
7x – 3.(-4x+2) = 5 ⇔ 7x + 12x – 6 = 5 ⇔ 19x = 11 ⇔ x= 11/19
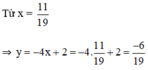
Vậy hệ phương trình có nghiệm duy nhất ( 11/19;-6/19)
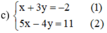
Từ (1) rút x theo y ta được: x = -3y – 2
Thế x = -3y – 2 vào phương trình (2) ta được :
5.(-3y – 2) – 4y = 11 ⇔ -15y – 10 – 4y = 11 ⇔ -19y = 21 ⇔ y = - 21/19
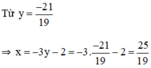
Vậy hệ phương trình có nghiệm duy nhất ( 25/19; -21/19)
Cách 2
Kiến thức áp dụng
Giải hệ phương trình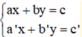 
ta làm như sau:
Bước 1: Từ một phương trình (coi là phương trình thứ nhất), ta biểu diễn x theo y (hoặc y theo x) ta được phương trình (*). Sau đó, ta thế (*) vào phương trình thứ hai để được một phương trình mới ( chỉ còn một ẩn)..
Bước 2: Dùng phương trình mới ấy thay thế cho phương trình thứ hai, phương trình (*) thay thế cho phương trình thứ nhất của hệ ta được hệ phương trình mới tương đương ..
Bước 3: Giải hệ phương trình mới ta tìm được nghiệm của hệ phương trình.
Đúng 0
Bình luận (0)
giải hệ phương trình\(\left\{{}\begin{matrix}x\sqrt{y}+y\sqrt{x}=30\\x\sqrt{x}+y\sqrt{y}=35\end{matrix}\right.\)
7 tháng 1 2022 lúc 16:11
Giải hệ phương trình sau: x.y + x+ y = 11 và x^2 .y + x.y^2 = 30
Cho hệ phương trình
x
+
0
y
-
2
5
x
-
y
-
9...
Đọc tiếp
Cho hệ phương trình x + 0 y = - 2 5 x - y = - 9
Nghiệm của hệ phương trình này có phải là nghiệm của phương trình 3x – 7y = 1 hay không?
Thay x = -2, y = -1 vào phương trình 3x – 7y = 1, ta có:
3.(-2) – 7.(-1) = -6 + 7 = 1
Vậy x và y thỏa phương trình 3x – 7y = 1 nên (x; y) = (-2; -1) là nghiệm của phương trình 3x – 7y = 1.
Đúng 0
Bình luận (0)
14 tháng 12 2020 lúc 12:36
giải hệ phương trình :
\(\left\{{}\begin{matrix}x^2+y^2=30\\x+y=6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x+y\right)^2-2xy=30\\x+y=6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}xy=3\\x+y=6\end{matrix}\right.\)
Thep Viet đảo, x và y là nghiệm:
\(t^2-6t+3=0\Rightarrow\left[{}\begin{matrix}t=3+\sqrt{6}\\t=3-\sqrt{6}\end{matrix}\right.\)
\(\Rightarrow\left(x;y\right)=\left(3+\sqrt{6};3-\sqrt{6}\right);\left(3-\sqrt{6};3+\sqrt{6}\right)\)
Đúng 0
Bình luận (0)
\(\hept{\begin{cases}x-5=3\\y+25x=12\end{cases}}\)
giải hệ phương trình bằng 2 cách
\(\hept{\begin{cases}x-5=3\\y+25x=12\end{cases}}\Leftrightarrow\hept{\begin{cases}x=8\\y+25.8=12\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=8\\y+200=12\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}y=-188\\x=8\end{cases}}\)
vậy hệ phương trình có nghiệm duy nhất \(\left(x;y\right)=\left(8;-188\right)\)
P/S bài này ko làm được 2 cách đâu Despacito nhé
Đúng 0
Bình luận (0)
Bạn ấy làm cách 1 rùi nên mk làm cách 2 nha !
C2:
hệ pt <=> 25x-125 = 75
y+25x = 12
<=> (25x-125)-(y-25) = 75-12
y+25x = 12
<=> -125-y = 63
y+25x = 12
<=> y = -188
x = 8
Vậy .............
Tk mk nha
Đúng 0
Bình luận (0)
giải hệ phương trình: 1/x+1/y=1/6 và 3/x+4/y=17/30
Cho hệ phương trình
x
+
0
y
-
2
5
x
-
y
-
9...
Đọc tiếp
Cho hệ phương trình x + 0 y = - 2 5 x - y = - 9
Minh họa hình học tập nghiệm của hệ phương trình đã cho. Từ đó xác định nghiệm của hệ.
Ta có:
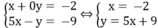
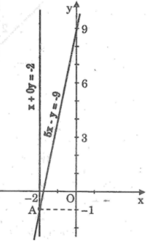
*Vẽ đường thẳng x = -2 song song với trục tung
*Vẽ đường thẳng y = 5x + 9
Cho x = 0 thì y = 9 ⇒ (0; 9)
Cho y = 0 thì x = - 9/5 = -1,8
Hai đường thẳng y = 5x + 9 và x = -2 cắt nhau tại A(-2; -1). Vậy hệ phương trình có một nghiệm duy nhất (x; y) = (-2; -1).
Đúng 0
Bình luận (0)
Giải hệ phương trình \(\hept{\begin{cases}x\sqrt{y}+y\sqrt{x}=30\\x\sqrt{x}+y\sqrt{y}=35\end{cases}}\)