Cách 1
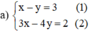
Từ (1) rút ra được y = x – 3
Thế vào phương trình (2) ta được:
3x – 4.(x – 3) = 2 ⇔ 3x – 4x + 12 = 2 ⇔ x = 10
Từ x = 10 ⇒ y = x – 3 = 7.
Vậy hệ phương trình có nghiệm duy nhất (10 ; 7).
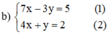
Từ (2) rút ra được y = -4x + 2.
Thế y = -4x + 2 vào phương trình (1) ta được :
7x – 3.(-4x+2) = 5 ⇔ 7x + 12x – 6 = 5 ⇔ 19x = 11 ⇔ x= 11/19
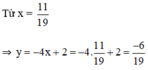
Vậy hệ phương trình có nghiệm duy nhất ( 11/19;-6/19)
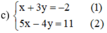
Từ (1) rút x theo y ta được: x = -3y – 2
Thế x = -3y – 2 vào phương trình (2) ta được :
5.(-3y – 2) – 4y = 11 ⇔ -15y – 10 – 4y = 11 ⇔ -19y = 21 ⇔ y = - 21/19
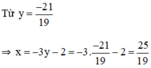
Vậy hệ phương trình có nghiệm duy nhất ( 25/19; -21/19)
Cách 2



Kiến thức áp dụng
Giải hệ phương trình 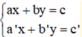 ta làm như sau:
ta làm như sau:
Bước 1: Từ một phương trình (coi là phương trình thứ nhất), ta biểu diễn x theo y (hoặc y theo x) ta được phương trình (*). Sau đó, ta thế (*) vào phương trình thứ hai để được một phương trình mới ( chỉ còn một ẩn)..
Bước 2: Dùng phương trình mới ấy thay thế cho phương trình thứ hai, phương trình (*) thay thế cho phương trình thứ nhất của hệ ta được hệ phương trình mới tương đương ..
Bước 3: Giải hệ phương trình mới ta tìm được nghiệm của hệ phương trình.








