Question

Giải các hệ phương trình sau:

a ) 2 ( x + y ) + 3 ( x − y ) = 4 ( x + y ) + 2 ( x − y ) = 5 b ) 2 ( x − 2 ) + 3 ( 1 + y ) = − 2 3 ( x − 2 ) − 2 ( 1 + y ) = − 3

Answer 1

Bài toán này có hai cách giải:

Cách 1: Thu gọn từng phương trình ta sẽ thu được phương trình bậc nhất hai ẩn x và y.

Cách 2: Đặt ẩn phụ.

Cách 1:

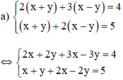
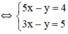 (hệ số của y bằng nhau nên ta trừ từng vế hai phương trình)

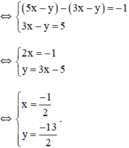
Vậy hệ phương trình có nghiệm duy nhất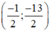 

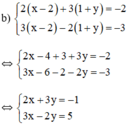
(Nhân hai vế pt 1 với 2; pt 2 với 3 để hệ số của y đối nhau)

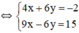 (Hệ số của y đối nhau nên ta cộng từng vế của hai pt)

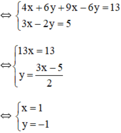
Vậy hệ phương trình có nghiệm duy nhất (1; -1).

Cách 2:

a) Đặt x + y = u và x – y = v (*)

Khi đó hệ phương trình trở thành

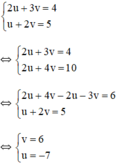
Thay u = -7 và v = 6 vào (*) ta được hệ phương trình:

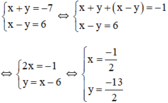
Vậy hệ phương trình có nghiệm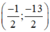 

b) Đặt x – 2 = u và y + 1 = v.

Khi đó hệ phương trình trở thành :

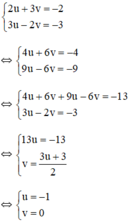
+ u = -1 ⇒ x – 2 = -1 ⇒ x = 1.

+ v = 0 ⇒ y + 1 = 0 ⇒ y = -1.

Vậy hệ phương trình có nghiệm (1; -1).