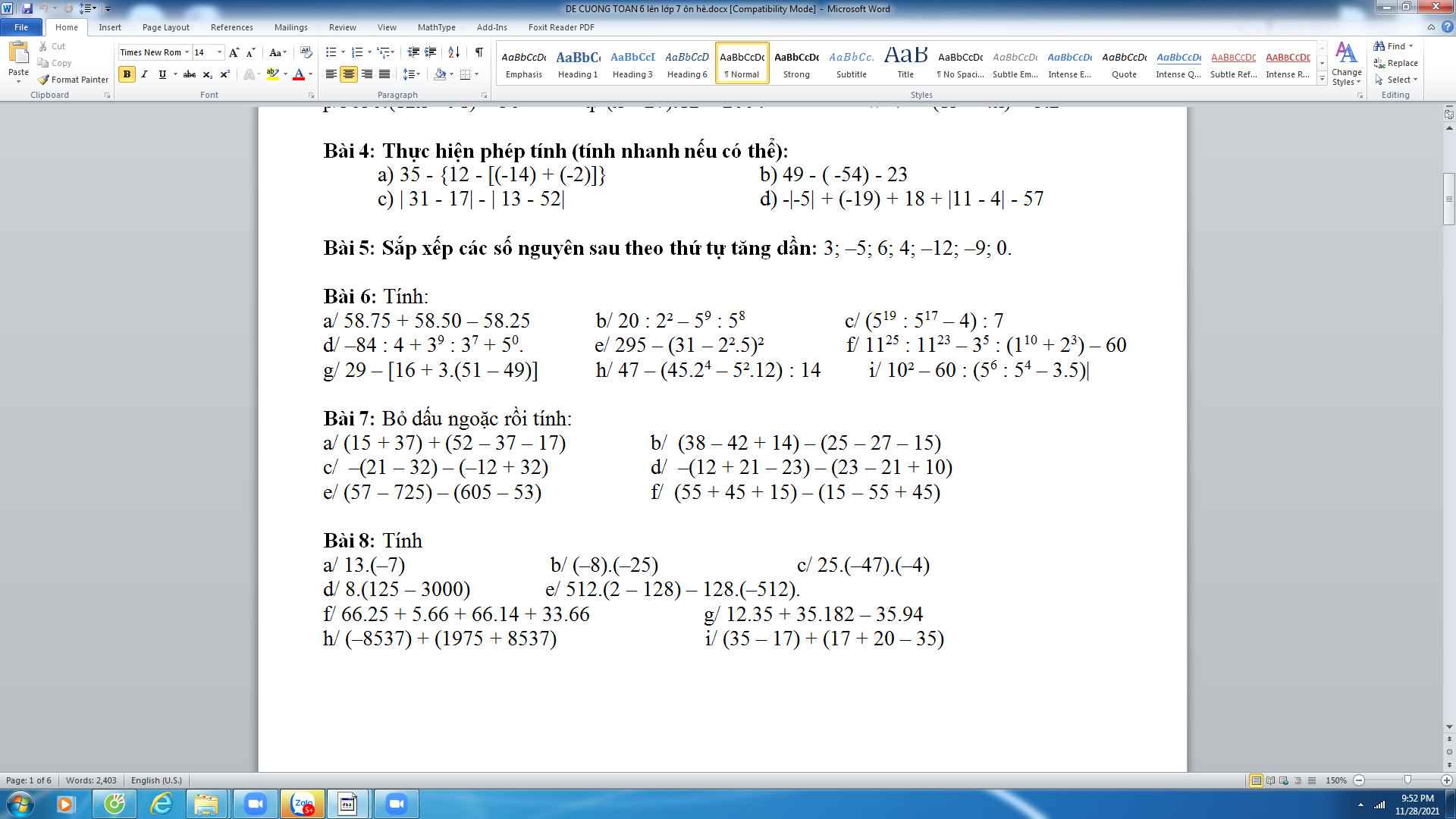
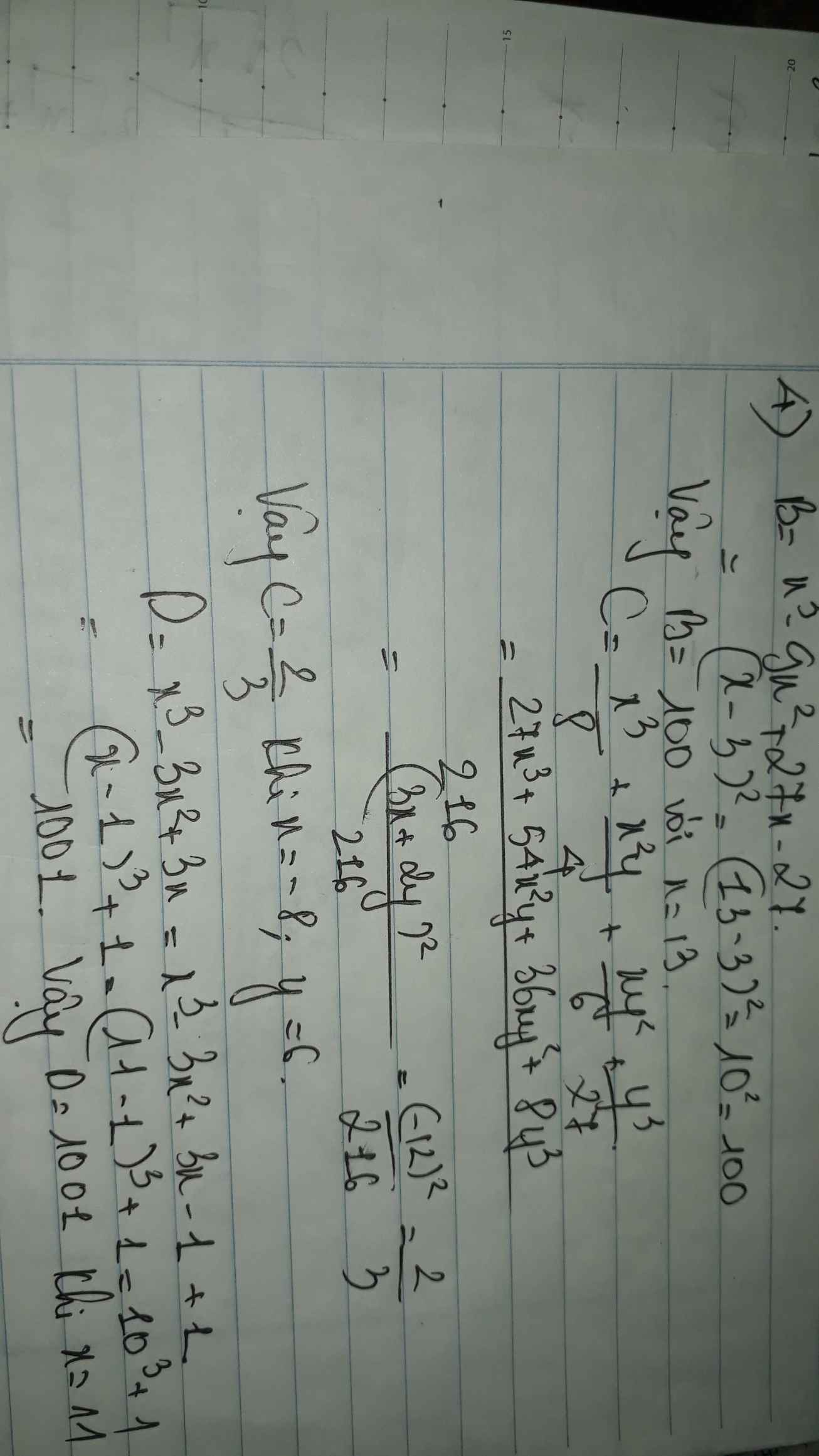 giúp mình câu D ,c bài 1
giúp mình câu D ,c bài 1

Những câu hỏi liên quan
 giúp mình làm bài 1 câu c,d ,e với ạ
giúp mình làm bài 1 câu c,d ,e với ạ
Đây là nội dung của bài 1 câu c, d, e:
**Câu c:**
\[
\begin{cases}
2x - 3y = 11 \\
-4x + 6y = 5
\end{cases}
\]
**Câu d:**
\[
\begin{cases}
3x + 2y = 1 \\
2x - y = 3
\end{cases}
\]
**Câu e:**
\[
\begin{cases}
2x + 5y = 2 \\
6x - 15y = 6
\end{cases}
\]
3: \(\begin{cases}2x-3y=11\\ -4x+6y=5\end{cases}\Rightarrow\begin{cases}4x-6y=22\\ -4x+6y=5\end{cases}\)
=>\(\begin{cases}4x-6y-4x+6y=22+5\\ 2x-3y=11\end{cases}\Rightarrow\begin{cases}0x=27\\ 2x-3y=11\end{cases}\)
=>(x;y)∈∅
4: \(\begin{cases}3x+2y=1\\ 2x-y=3\end{cases}\Rightarrow\begin{cases}3x+2y=1\\ 4x-2y=6\end{cases}\)
=>\(\begin{cases}3x+2y+4x-2y=1+6=7\\ 2x-y=3\end{cases}\Rightarrow\begin{cases}7x=7\\ y=2x-3\end{cases}\)
=>\(\begin{cases}x=1\\ y=2\cdot1-3=2-3=-1\end{cases}\)
5: \(\begin{cases}2x+5y=2\\ 6x-15y=6\end{cases}\Rightarrow\begin{cases}6x+15y=6\\ 6x-15y=6\end{cases}\)
=>\(\begin{cases}6x+15y+6x-15y=6+6=12\\ 2x+5y=2\end{cases}=.\begin{cases}12x=12\\ 5y=2-2x\end{cases}\)
=>\(\begin{cases}x=1\\ 5y=2-2\cdot1=0\end{cases}\Rightarrow\begin{cases}x=1\\ y=0\end{cases}\)
Đúng 0
Bình luận (0)
giúp mình bài 6 với ạ trừ câu a còn các câu b,c,d, giúp mình với ạ
Đọc tiếp
giúp mình bài 6 với ạ trừ câu a còn các câu b,c,d, giúp mình với ạ
\(b,N=\left(2x-1\right)^2-4\ge-4\\ N_{min}=-4\Leftrightarrow x=\dfrac{1}{2}\\ c,P=\left(2x-5\right)^2+6\left(2x-5\right)+9-4\\ P=\left(2x-5+3\right)^2-4=\left(2x-2\right)^2-4\ge-4\\ P_{min}=-4\Leftrightarrow x=1\\ d,Q=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1\\ Q=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1\\ Q_{min}=1\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
Đúng 4
Bình luận (0)
6a.
$M=x^2-x+1=(x^2-x+\frac{1}{4})+\frac{3}{4}$
$=(x-\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}$
Vậy $M_{\min}=\frac{3}{4}$ khi $x-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{2}$
Đúng 1
Bình luận (0)
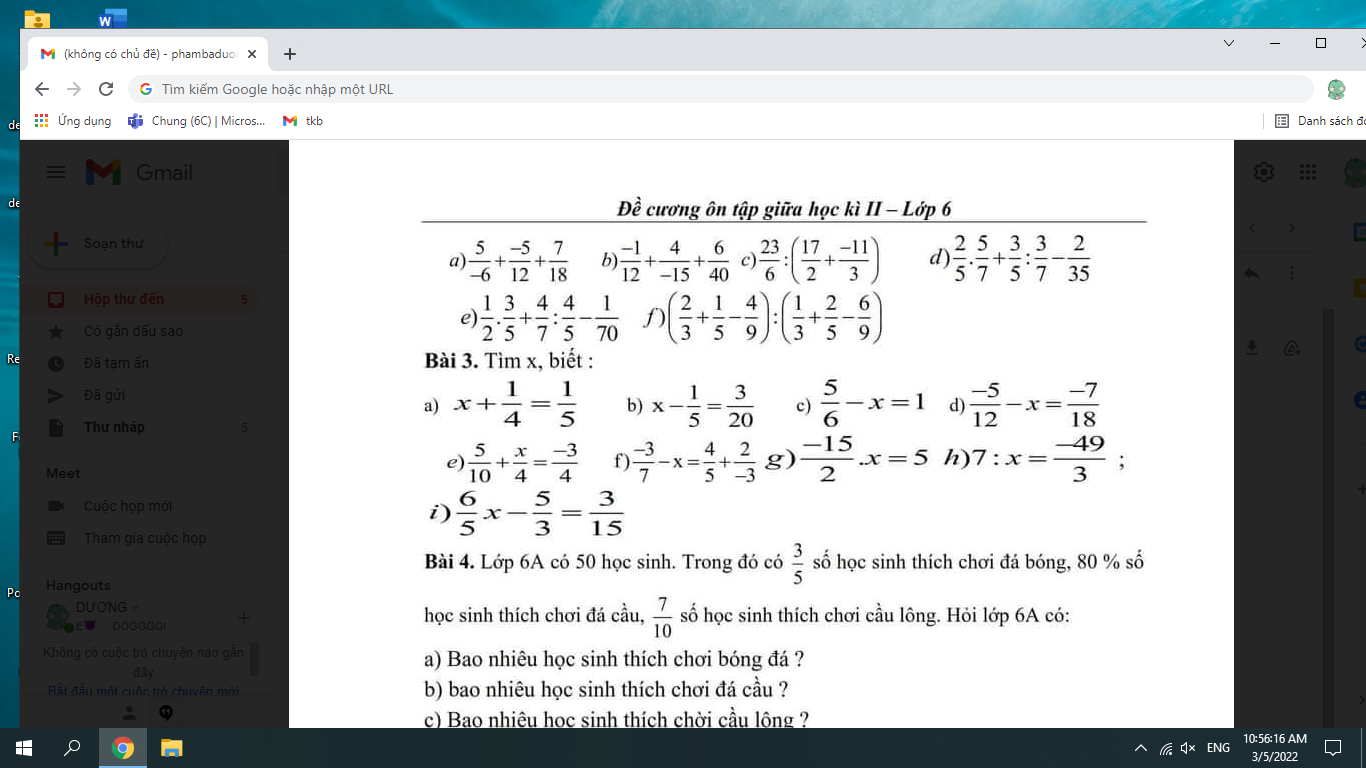 giúp mình câu a ,b,c,d bài phía trên bài 3 nhé
giúp mình câu a ,b,c,d bài phía trên bài 3 nhé
a: x+1/4=1/5
=>x=1/5-1/4
=>x=-1/20
b: x-1/5=3/20
=>x=3/20+1/5
=>x=3/20+4/20=7/20
c: \(\dfrac{5}{6}-x=1\)
=>x=5/6-1=-1/6
Đúng 1
Bình luận (0)
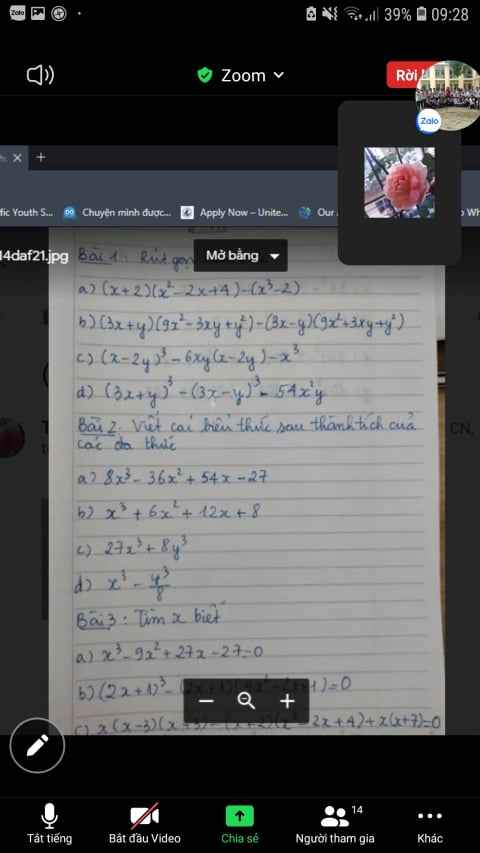
làm giúp mình bài 2 với câu d bài 1 vs ạ
Bài 2:
a: \(8x^3-36x^2+54x-27=\left(2x-3\right)^3\)
b: \(x^3+6x^2+12x+8=\left(x+2\right)^3\)
c: \(27x^3+8y^3=\left(3x+2y\right)\left(9x^2-6xy+4y^2\right)\)
d: \(x^3-\dfrac{y^3}{8}=\left(x-\dfrac{1}{2}y\right)\left(x^2+\dfrac{1}{2}xy+\dfrac{1}{4}y^2\right)\)
Đúng 2
Bình luận (0)
Giúp mình với câu D, e, f bài 1 với bài 2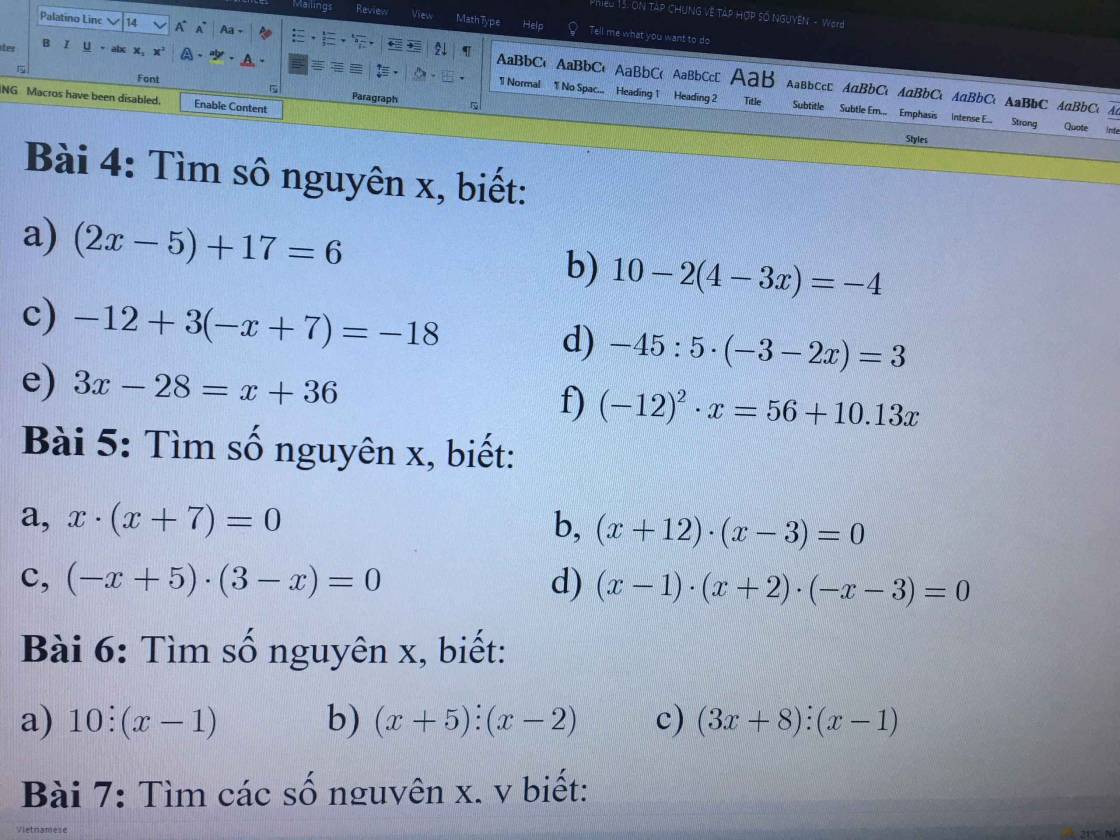
Xem thêm câu trả lời
 giúp mình bài 4 câu B,C D với ạ
giúp mình bài 4 câu B,C D với ạ
Bài 4:
c) Ta có: \(\dfrac{x^3}{8}+\dfrac{x^2y}{2}+\dfrac{xy^2}{6}+\dfrac{y^3}{27}\)
\(=\left(\dfrac{x}{2}\right)^3+3\cdot\left(\dfrac{x}{2}\right)^2\cdot\dfrac{y}{3}+3\cdot\dfrac{x}{2}\cdot\left(\dfrac{y}{3}\right)^2+\left(\dfrac{y}{3}\right)^3\)
\(=\left(\dfrac{1}{2}x+\dfrac{1}{3}y\right)^3\)
\(=\left(\dfrac{-1}{2}\cdot8+\dfrac{1}{3}\cdot6\right)^3=\left(-4+2\right)^3=-8\)
Đúng 0
Bình luận (0)
Bài 6:
a) Ta có: \(P=\left(x+2\right)^3+\left(x-2\right)^3-2x\left(x^2+12\right)\)
\(=x^3+6x^2+12x+8+x^3-6x^2+12x-8-2x^3-12x\)
=0
b) Ta có: \(Q=\left(x-1\right)^3-\left(x+1\right)^3+6\left(x+1\right)\left(x-1\right)\)
\(=x^3-3x^2+3x-1-x^3-3x^2-3x-1+6x^2-6\)
=-8
Đúng 0
Bình luận (0)
Giải giúp mình bài hình câu c , d với ạ
 giúp mình bài 2 câu c với d vs ạ
giúp mình bài 2 câu c với d vs ạ
Lời giải:
c.
$4(x+5)^3-7=101$
$4(x+5)^3=101+7=108$
$(x+5)^3=108:4=27=3^3$
$\Rightarrow x+5=3$
$\Rightarrow x=-2$
d.
$2^{x+1}.3+15=39$
$2^{x+1}.3=39-15=24$
$2^{x+1}=24:3=8=2^3$
$\Rightarrow x+1=3$
$\Rightarrow x=2$
Đúng 0
Bình luận (0)
Mng giúp mình bài 4 câu c, d) bài 5 luôn nha. Cảm ơn bạn 🤩
a, Xét Δ ABC, có :
\(BC^2=AB^2+AC^2\) (định lí Py - ta - go)
=> \(BC^2=10^2+8^2\)
=> \(BC^2=164\)
=> \(BC=12,8\left(cm\right)\)
b, Xét Δ ABE và Δ HBE, có :
\(\widehat{ABE}=\widehat{HBE}\) (BE là tia phân giác \(\widehat{ABC}\))
\(\widehat{BAE}=\widehat{BHE}=90^o\)
BE là cạnh chung
=> Δ ABE = Δ HBE (g.c.g)
=> AB = HB
Xét Δ ABH, có : AB = HB (cmt)
=> Δ ABH cân tại B
c,
Gọi O là giao điểm của tia AH và BE
Xét Δ cân ABH, có :
BO là tia phân giác \(\widehat{ABH}\)
=> BO là đường cao
=> \(BO\perp AH\)
=> \(BE\perp AH\)
Đúng 2
Bình luận (1)