Bài 4:
c) Ta có: \(\dfrac{x^3}{8}+\dfrac{x^2y}{2}+\dfrac{xy^2}{6}+\dfrac{y^3}{27}\)
\(=\left(\dfrac{x}{2}\right)^3+3\cdot\left(\dfrac{x}{2}\right)^2\cdot\dfrac{y}{3}+3\cdot\dfrac{x}{2}\cdot\left(\dfrac{y}{3}\right)^2+\left(\dfrac{y}{3}\right)^3\)
\(=\left(\dfrac{1}{2}x+\dfrac{1}{3}y\right)^3\)
\(=\left(\dfrac{-1}{2}\cdot8+\dfrac{1}{3}\cdot6\right)^3=\left(-4+2\right)^3=-8\)
Bài 6:
a) Ta có: \(P=\left(x+2\right)^3+\left(x-2\right)^3-2x\left(x^2+12\right)\)
\(=x^3+6x^2+12x+8+x^3-6x^2+12x-8-2x^3-12x\)
=0
b) Ta có: \(Q=\left(x-1\right)^3-\left(x+1\right)^3+6\left(x+1\right)\left(x-1\right)\)
\(=x^3-3x^2+3x-1-x^3-3x^2-3x-1+6x^2-6\)
=-8

 giúp mình bài 4 câu B,C D với ạ
giúp mình bài 4 câu B,C D với ạ


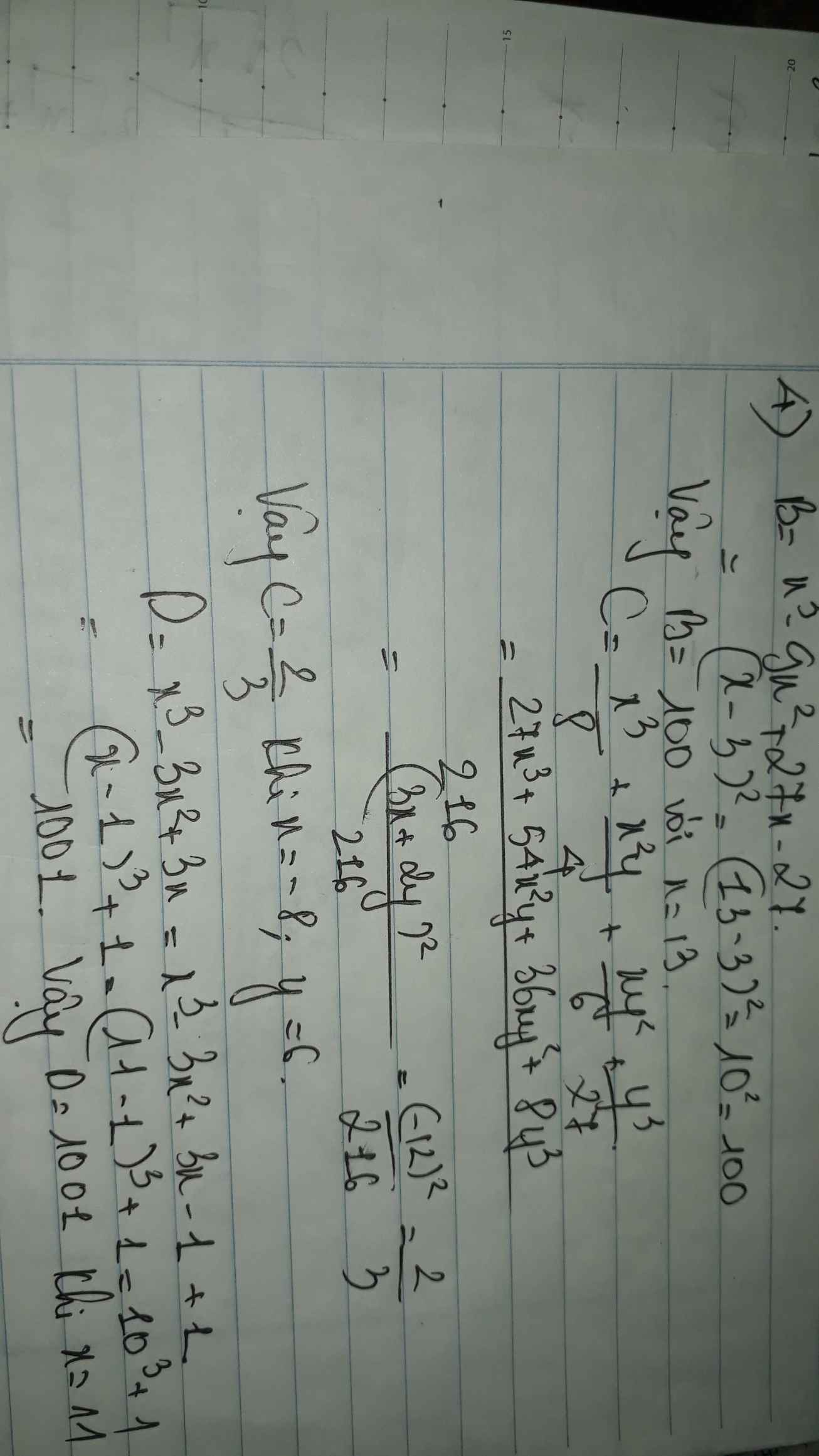










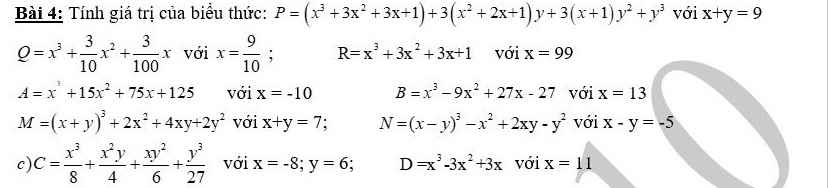

 giải giúp bài 10 ạ
giải giúp bài 10 ạ