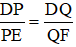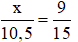cho tam giác def df=24cm lấy p,q lần lượt thuộc de,df sao cho ep=10.5 và dq=9cm biết pq//ef tính dp

Những câu hỏi liên quan
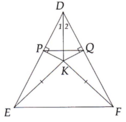
Cho tam giác DEF có DE = DF. Lấy điểm K nằm trong tam giác sao cho KE = KF. Kẻ KP vuông góc với DE (P thuộc DE), KQ vuông góc với DF (Q thuộc DF). Chứng minh:
a) K thuộc đường trung trực của EF và PQ;
b) DK là đường trung trực của EF và PQ. Từ đó suy ra PQ//EF.
Cho tam giác DEF, kẻ MN song song với EF (M ∈ DE; N ∈ DF). Biết ME = 10cm; DN = 9cm; DF = 24cm. Tính DM=?
Ta có: \(NF=DF-DN=24-9=15cm\)
Áp dụng định lí Ta-let vào \(\Delta DEF\) có MN//EF: \(\dfrac{DM}{ME}=\dfrac{DN}{NF}\Leftrightarrow\dfrac{DM}{10}=\dfrac{9}{15}\Rightarrow DM=6\left(cm\right)\)
Đúng 1
Bình luận (0)
Bài 1:
Cho tam giác DEF nhọn. DE<DF, lấy M thuộc cạnh DE, N thuộc cạnh DF sao cho MN//EF. Cho biết DM=2cm, DN=3,5cm. Tính NF.
Bài 2:
Cho tam giác DEF nhọn, DE<DF. Lấy K thuộc cạnh DE, I thuộc cạnh DF sao cho KI//EF. Cho biết DK=3cm, KE=1cm, DI=4,2cm. Tính IF.
1) tam giác DEF có MN//EF
=> \(\frac{DM}{ME}=\frac{DN}{NF}=>\frac{2}{2}=\frac{3,5}{NF}=>NF=\frac{3,5.2}{2}=3,5cm\)
2)tam giasc DEF cos KI//EF
=>\(\frac{DK}{KE}=\frac{DI}{IF}=\frac{3}{1}=\frac{4,2}{IF}=IF=\frac{1.4,2}{3}=1,4cm\)
Câu 1: Cho tam giác DEF vuông tại D có DE = 12cm, DF = 9cm, DM là đường trung tuyến (M thuộc EF). a) Tính EF, DM. b) Gọi N và K lần lượt là chân các đường vuông góc hạ từ M xuống DE và DF. Tứ giác DNMK là hình gì? Vì sao? c) Gọi H là điểm đối xứng với M qua N, O là trung điểm của MD. Chứng minh rằng ba điểm H, O, F thẳng hàng rồi.
a: ΔDEF vuông tại D
=>\(DE^2+DF^2+EF^2\)
=>\(EF^2=9^2+12^2=225\)
=>\(EF=\sqrt{225}=15\left(cm\right)\)
Ta có; ΔDEF vuông tại D
mà DM là đường trung tuyến
nên \(DM=\dfrac{EF}{2}=7,5\left(cm\right)\)
b: Xét tứ giác DNMK có
\(\widehat{DNM}=\widehat{DKM}=\widehat{KDN}=90^0\)
=>DNMK là hình chữ nhật
c: Xét ΔDEF có MN//DF
nên \(\dfrac{MN}{DF}=\dfrac{EM}{EF}\)
=>\(\dfrac{MN}{DF}=\dfrac{1}{2}\)
mà \(MN=\dfrac{1}{2}MH\)
nên MH=DF
Ta có: MN//DF
N\(\in\)MH
Do đó: MH//DF
Xét tứ giác DHMF có
MH//DF
MH=DF
Do đó: DHMF là hình bình hành
=>DM cắt HF tại trung điểm của mỗi đường
mà O là trung điểm của DM
nên O là trung điểm của HF
=>H,O,F thẳng hàng
Đúng 1
Bình luận (0)
cho tam giác DEF có DE =9cm , DF = 15 cm , EF = 21 cm . lấy M,N, thuộc DE , DF sao cho DM = 3cm , DN = 5cm
a, chứng minh MN //EF
b, Tính MN
c, kẻ trung tuyến DI của tam giác DEF . DI cắt MN tại K . Chứng minh K là trung điểm MN
a)Cho tam giác AEF có PQ//EF, biết DF=24cm, QF=15cm, DP=6,3cm. Tính PE b)cho tam giác MNK trên đoạn MN lấy điểm E, trên đoạn NK lấy điểm F sao cho EF//MK. Biết NE=5cm,MN=7,5cm, FK=2cm. Tính NF
a: D ở đâu vậy bạn?
b: EN+EM=MN
=>EM=7,5-5=2,5cm
Xét ΔNMK có EF//MK
nên NE/EM=NF/FK
=>NF/2=5/2,5=2
=>NF=4(cm)
Đúng 0
Bình luận (0)
Cho tam giác DEF nhọn, DE<DF . Lấy M thuộc cạnh DE , N thuộc cạnh DF sao cho MN//EF. Cho biết DM=2cm , DN=3,5cm . Tính NF?
Bài 4. Cho tam giác DEF vuông tại D có DE = 9cm DF = 12cm Tia phân giác của góc D cắt EF tại P. Từ P kẻ PH vuông góc DF (H thuộc DF). a) Tính tỉ số (EP)/(FP) b) Tìm các cặp tam giác đồng dạng có trong hình vẽ và tỉ số đồng dạng. c) Tính PH.
a: EP/FP=DE/DF=3/4
b: Xet ΔFHP vuông tại H và ΔFDE vuông tại D có
góc HFP chung
=>ΔFHP đồng dạng vơi ΔFDE
c: ΔFHP đồng dạng với ΔFDE
=>HP/DE=FP/FE=4/7
=>HP/9=4/7
=>HP=36/7(cm)
Đúng 2
Bình luận (0)
a: EP/FP=DE/DF=3/4
b: Xet ΔFHP vuông tại H và ΔFDE vuông tại D có
góc HFP chung
=>ΔFHP đồng dạng vơi ΔFDE
c: ΔFHP đồng dạng với ΔFDE
=>HP/DE=FP/FE=4/7
=>HP/9=4/7
=>HP=36/7(cm)
Đúng 2
Bình luận (0)
Cho tam giác DEF(DE<DF).P thuộc DE,Q thuộc DF sao cho PQ//EF.Có :PE=10,5 cm.DQ=9 cm.DF=24 cm.Tính x(DP)
Hình bạn tự vẽ nhé!
Ta có PQ // EF
Áp dụng định lý Talet trong tam giác DEF ta có:
Mà DP = x, PE = 10,5 ; DQ = 9 ; QF = DF – DQ = 24 – 9 = 15
Do đó ta có :
⇒ 15x = 9.10,5
⇔ 15x = 94,5
⇔ x = 94,5:15 = 6,3
Vậy x = 6,3.