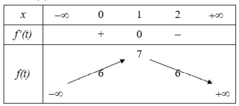
số giá trị nguyên của tham số m để phương trình x2-2x|x-3| =m có 3 nghiệm

Những câu hỏi liên quan
Cho phương trình: 3\(\sqrt{x^2-2x+3}\) =x2-2x+m với tham số m∈R.Tìm tất cả các giá trị của tham số m để phương trình đã cho có đúng hai nghiệm phân biệt thuộc đoạn 0,3
- Đặt \(a=x^2-2x\left(a\ge-1\right)\)
PTTT \(3\sqrt{a+3}=a+m\left(a\ge-m\right)\)
\(\Leftrightarrow9\left(a+3\right)=\left(a+m\right)^2=a^2+2am+m^2=9a+27\)
\(\Leftrightarrow a^2+a\left(2m-9\right)+m^2-27=0\)
Có : \(\Delta=\left(2m-9\right)^2-4\left(m^2-27\right)=4m^2-36m+81-4m^2+108\)
\(=-36m+189\)
- Để phương trình đề có 2 nghiệm phân biệt :
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta>0\\\left(a_1+1\right)\left(a_2+1\right)>0\\a_1+1+a_2+1>0\end{matrix}\right.\)
Lại có : Theo vi ét : \(\left\{{}\begin{matrix}a_1+a_2=-2m+9\\a_1a_2=m^2-27\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\Delta>0\\a_1a_2+a_1+a_2+1>0\\a_1+a_2+2>0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}-36m+189>0\\m^2-27-2m+9+1=m^2-2m-17>0\\-2m+9+2=-2m+11>0\end{matrix}\right.\)
\(\Rightarrow m=\left(-\infty;1-3\sqrt{2}\right)\cup\left(1+3\sqrt{2};\dfrac{21}{4}\right)\) ( * )
- Có : \(x^2-2x=a\)
- Đặt \(f\left(x\right)=x^2-2x\)
- Ta có đồ thị \(x^2-2x=0\)
- Từ độ thị hàm số : Để phương trình \(x^2-2x=a\) có 2 nghiệm phân biệt trong đoạn 0, 3 thì \(a=(-1;0]\)
Lại có : \(a=[-m;+\infty)\)
\(\Rightarrow-m\le0\)
\(\Rightarrow m\ge0\)
- Kết hợp với ( * )
\(\Rightarrow m\in\left(1+3\sqrt{2};\dfrac{21}{4}\right)\)
Vậy ...
Đúng 2
Bình luận (0)
Cho phương trình x²- 2x + m - 1 = 0 với M là tham số a, Tìm tất cả giá trị của tham số m để phương trình có hai nghiệm phân biệt x1 x2 thỏa mãn x1²+x2²-3x1x2= 2m²+|m-3|
Δ=(-2)^2-4(m-1)
=-4m+4+4
=-4m+8
Để phương trình có hai nghiệm phân biệt thì -4m+8>0
=>-4m>-8
=>m<2
x1^2+x2^2-3x1x2=2m^2+|m-3|
=>2m^2+|m-3|=(x1+x2)^2-5x1x2=2^2-5(m-1)=4-5m+5=-5m+9
TH1: m>=3
=>2m^2+m-3+5m-9=0
=>2m^2+6m-12=0
=>m^2+3m-6=0
=>\(m\in\varnothing\)
TH2: m<3
=>2m^2+3-m+5m-9=0
=>2m^2+4m-6=0
=>m^2+2m-3=0
=>(m+3)(m-1)=0
=>m=1 hoặc m=-3
Đúng 0
Bình luận (0)
Có bao nhiêu giá trị nguyên của tham số m để phương trình
log
2
(
x
2
-
2
x
+
5
)
-
m
.
log
x
2
-
2
x
+
5
2
5
có hai nghiệm phân biệ...
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m để phương trình log 2 ( x 2 - 2 x + 5 ) - m . log x 2 - 2 x + 5 2 = 5 có hai nghiệm phân biệt là nghiệm của bất phương trình log 2017 ( x + 1 ) - log 2017 ( x - 1 ) > log 2017 4
A. 0
B. 1
C. 3
D. 2
Cho phương trình (2m−5)x2 −2(m−1)x+3=0 (1); với m là tham số thực
1) Tìm m để phương trình (1) có một nghiệm bằng 2, tìm nghiệm còn lại.
3) Tìm giá trị của m để phương trình đã cho có nghiệm
4) Xác định các giá trị nguyên của để phương trình đã cho có hai nghiệm phân biệt đều nguyên dương
1) điều kiện của m: m khác 5/2
thế x=2 vào pt1 ta đc:
(2m-5)*4 - 4(m-1)+3=0 <=> 8m-20-4m+4+3=0<=> 4m = 13 <=> m=13/4 (nhận)
lập △'=[-(m-1)]2-*(2m-5)*3 = (m-4)2
vì (m-4)2 ≥ 0 nên phương trình có nghiệm kép => x1= x2 =2
3) vì △'≥0 với mọi m nên phương trình đã cho có nghiệm với mọi m
Đúng 1
Bình luận (0)
Cho bất phương trình
3
+
x
+
1
-
x
≤
m
+
1
-
x
2
-
2
x
. Tìm tất cả các giá trị thực của tham số m để bất phương trình có nghiệm thực. A.
m
≥
25
4
B....
Đọc tiếp
Cho bất phương trình 3 + x + 1 - x ≤ m + 1 - x 2 - 2 x . Tìm tất cả các giá trị thực của tham số m để bất phương trình có nghiệm thực.
A. m ≥ 25 4
B. m ≥ 4
C. m ≥ 6
D. m ≥ 7
Cho phương trình
log
0
,
5
m
+
6
x
+
log
2
3
−
2
x
−
x
2
0
(m là tham số). Có bao nhiêu giá trị nguyên...
Đọc tiếp
Cho phương trình log 0 , 5 m + 6 x + log 2 3 − 2 x − x 2 = 0 (m là tham số). Có bao nhiêu giá trị nguyên dương của m để phương trình có nghiệm thực?
A. 17
B. 18
C. 23
D. 15
Đáp án A
Ta có:
log 0 , 5 m + 6 x + log 2 3 − 2 x − x 2 = 0 ⇔ − log 2 m + 6 x + log 2 3 − 2 x − x 2 = 0
⇔ log 2 m + 6 x = log 2 3 − 2 x − x 2 ⇔ 3 − 2 x − x 2 > 0 m + 6 x = 3 − 2 x − x 2 ⇔ 1 > x > − 3 m = − x 2 − 8 x + 3 = f x
Xét hàm số f x = − x 2 − 8 x + 3 trên khoảng − 3 ; 1 ta có:
f ' x = − 2 x − 8 < 0 ∀ x ∈ − 3 ; 1
Lại có: f − 3 = 18 ; f 1 = − 6
Suy ra PT có nghiệm khi m ∈ − 6 ; 18 ⇒ có 17 giá trị nguyên dương của m thỏa mãn yêu cầu bài toán.
Đúng 0
Bình luận (0)
Có bao nhiêu giá trị nguyên của tham số (m ) thuộc đoạn [ - 2018;2018 ] để phương trình x2 + (2 - m )x + 4 =4\(\sqrt{x^3+4x}\)có nghiệm là
ĐKXĐ: \(x\ge0\)
- Với \(x=0\) ko phải là nghiệm
- Với \(x>0\) chia 2 vế cho \(x\) ta được:
\(\dfrac{x^2+4}{x}+2-m=4\sqrt{\dfrac{x^2+4}{x}}\)
Đặt \(\sqrt{\dfrac{x^2+4}{x}}=t\ge2\)
\(\Rightarrow t^2-4t+2=m\)
Xét hàm \(f\left(t\right)=t^2-4t+2\) với \(t\ge2\)
\(\Rightarrow f\left(t\right)\ge f\left(2\right)=-2\Rightarrow m\ge-2\)
Có \(2018-\left(-2\right)+1=2021\) giá trị nguyên của m
Đúng 2
Bình luận (0)
Cho phương trình: x2-2x+m-3=0, với m là tham số. Tìm các giá trị của m để phương trình có hai nghiệm x1, x2 thỏa mãn: x12 + x22 - x1x2 < 7.
Δ=(-2)^2-4(m-3)
=4-4m+12=-4m+16
Để pt có hai nghiệm thì -4m+16>=0
=>-4m>=-16
=>m<=4
x1^2+x2^2-x1x2<7
=>(x1+x2)^2-3x1x2<7
=>2^2-3(m-3)<7
=>4-3m+9<7
=>-3m+13<7
=>-3m<-6
=>m>2
=>2<m<=4
Đúng 0
Bình luận (0)
Giá trị của tham số m để phương trình
4
x
−
m
.2
x
+
1
+
2
m
0
có 2 nghiệm
x
1
,
x
2
thỏa mãn
x
1
+...
Đọc tiếp
Giá trị của tham số m để phương trình 4 x − m .2 x + 1 + 2 m = 0 có 2 nghiệm x 1 , x 2 thỏa mãn x 1 + x 2 = 3 là:
A. m = 2
B. m = 3
C. m = 1
D. m = 4
Đáp án D
Ta có: 4 x − m .2 x + 1 + 2 m = 0 ⇔ 2 x 2 − 2 m .2 x + 2 m = 0
Giả thiết ⇔ Δ ' = m 2 − 2 m > 0 S = 2 m > 0 P = 2 m > 0 ⇔ m > 2
Khi đó: 2 x 1 + 2 x 2 = 2 m 2 x 1 .2 x 2 = 2 m ⇔ 2 x 1 + x 2 = 2 m ⇔ m = 4
Đúng 0
Bình luận (0)