Cho a, b, c là các số thực, theo thứ tự lập thành cấp số nhân.
Biết a + b + c = 26 a 2 + b 2 + c 2 = 364 . Tìm b.
A. b = -1
B. b = 10
C. b = 6
D. b = 4
Cho a, b, c là các số thực, theo thứ tự lập thành cấp số nhân.
Biết a + b + c = 26 a 2 + b 2 + c 2 = 364 Tìm b.
A. 9
B. 7
C. 6
D. 5
Chọn C.
Ta có
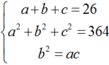
Từ đó ta có
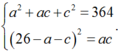
Đặt 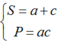 có hệ
có hệ
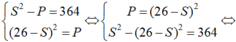
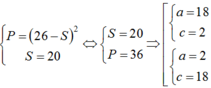
Vậy b2 = ac = 36 nên b = 6.
Cho ba số thực a, b, c khác 0. Xét các phát biểu sau
(1) Nếu a, b, c theo thứ tự đó lập thành cấp số cộng
(công sai khác 0) thì ba số 1 a , 1 b , 1 c theo thứ tự đó
cũng lập thành cấp số cộng
(2) Nếu a, b, c theo thứ tự đó lập thành cấp số nhân
thì ba số 1 a , 1 b , 1 c theo thứ tự đó cũng lập thành cấp
số nhân.
Khẳng định nào sau đây là đúng ?
A. (1) đúng, (2) sai
B. cả (1) và (2) đúng
C. cả (1) và (2) sai
D. (2) đúng, (1) sai
Biết rằng x; y là các số thực sao cho các số x; 2x- 3; y theo thứ tự lập thành một cấp số cộng và các số x 2 ; xy − 6 y ; y 2 theo thứ tự lập thành một cấp số nhân. Cặp số (x;y) là
A. 7 ; 3 7 và − 7 ; − 3 7
B. - 7 ; 3 7 và 7 ; − 3 7
C. 2 ; 3 2 và − 2 ; − 3 2
D. - 2 ; 3 7 và 2 ; 3 7
cho hai số dương a và b biết rằng ba số 1; a+8; b theo thứ tự lập thành cấp số công và ba số 1; a; b theo thứ tự lập thành cấp số nhân. tính giá trị a+b?
Do 3 số lập thành 1 CSC nên: \(2\left(a+8\right)=1+b\Rightarrow b=2a+15\)
Do 3 số lập thành 1 CSN nên:
\(a^2=b.1\Leftrightarrow a^2=2a+15\)
\(\Leftrightarrow a^2-2a-15=0\Rightarrow\left[{}\begin{matrix}a=5\\b=-3< 0\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow b=2a+15=25\)
Các số a,b,c (theo thứ tự đó) lập thành một cấp số nhân có tổng bằng 26. Tìm các số đó biết rằng: nếu một cấp số cộng có a là số hạng thứ nhất, b là số hạng thứ ba thì c là số hạng thứ chín
Gọi công bội của cấp số nhân là q => b=a.q; c=a.q^2
Gọi công sai của cấp số cộng là d => b=a+2d; c=a+8d
Ta có: a.q=a+2d => \(q=\dfrac{a+2d}{a}=1+2\dfrac{d}{a}\)
\(a.q^2=a+8d\Rightarrow q^2=\dfrac{a+8d}{a}=1+8\dfrac{d}{a}\)
Suy ra \(\left(1+2\dfrac{d}{a}\right)^2=1+8\dfrac{d}{a}\Rightarrow\dfrac{d}{a}=1\left(d\ne0\right)\)
=> b=a+2a=3a; c=a+8a=9a
Theo bài ra a+b+c=26 => a+3a+9a=13a=26 => a=2; b=6; c=18
Vậy ba số cần tìm là a=2; b=6; c=18
Cho bốn số a,b,c,d biết rằng a,b,c theo thứ tự đó lập thành một cấp số nhân công bội q>1; còn b,c,d theo thứ tự đó lập thành cấp số cộng. Tìm q biết rằng a+d=14 và b+c=12. Giúp mình với mng ơi <3
cho 4 số a b c d theo thứ tự lập thành 1 cấp số cộng và 4 số a-2, b-6, c-7, d-2 theo thứ tự là 1 cấp số nhân. Tìm a b c d
Ba số \(\frac{2}{{b - a}},\frac{1}{b},\frac{2}{{b - c}}\) theo thứ tự lập thành cấp số cộng. Chứng minh rằng ba số \(a,b,c\) theo thứ tự lập thành cấp số nhân.
Ba số \(\frac{2}{{b - a}},\frac{1}{b},\frac{2}{{b - c}}\) theo thứ tự lập thành cấp số cộng nên ta có:
\(\begin{array}{l}\frac{2}{{b - a}} + \frac{2}{{b - c}} = 2.\frac{1}{b} \Leftrightarrow \frac{1}{{b - a}} + \frac{1}{{b - c}} = \frac{1}{b} \Leftrightarrow \frac{{\left( {b - c} \right) + \left( {b - a} \right)}}{{\left( {b - a} \right)\left( {b - c} \right)}} = \frac{1}{b}\\ \Leftrightarrow \frac{{b - c + b - {\rm{a}}}}{{{b^2} - ab - bc + ac}} = \frac{1}{b} \Leftrightarrow \frac{{2b - c - {\rm{a}}}}{{{b^2} - ab - bc + ac}} = \frac{1}{b} \Leftrightarrow b\left( {2b - c - {\rm{a}}} \right) = {b^2} - ab - bc + ac\\ \Leftrightarrow 2{b^2} - bc - {\rm{ab}} = {b^2} - ab - bc + ac \Leftrightarrow {b^2} = {\rm{a}}c\end{array}\).
Vậy ba số \(a,b,c\) theo thứ tự lập thành cấp số nhân.
Cho dãy số tăng a, b, c theo thứ tự thành lập cấp số nhân, đồng thời a , b + 8 , c tạo thành cấp số cộng và a , b + 8 , c + 64 lập thành cấp số nhân. Khi đó giá trị của a − b + 2 c bằng
A. 184
B. 64
C. 92
D. 32