tìm tung độ đỉnh, vẽ đồ thị hàm số y= 4x^2 -1/4x

Những câu hỏi liên quan
Cho hàm số y= 1/4x^2 có đồ thị là (P)
a) Vẽ đồ thị (P) trên mặt phẳng tọa độ Oxy
b) Tìm hoành độ của điểm M thuộc đồ thị (P) biết M có tung độ bằng 100
a) Bảng giá trị:

Đồ thị:
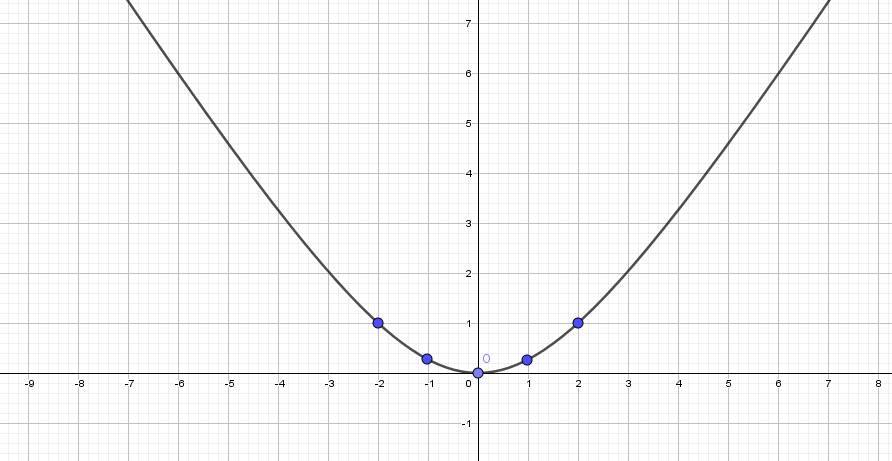
b) Thay y = 100 vào (P) ta được:
\(\dfrac{1}{4}x^2=100\)
\(\Leftrightarrow x^2=100:\dfrac{1}{4}\)
\(\Leftrightarrow x^2=400\)
\(\Leftrightarrow\left[{}\begin{matrix}x=20\\x=-20\end{matrix}\right.\)
Vậy M(-20; 100) hoặc M(20; 100)
Đúng 1
Bình luận (0)
b: y=100
=>1/4x^2=100
=>x^2=400
=>x=20 hoặc x=-20
a: 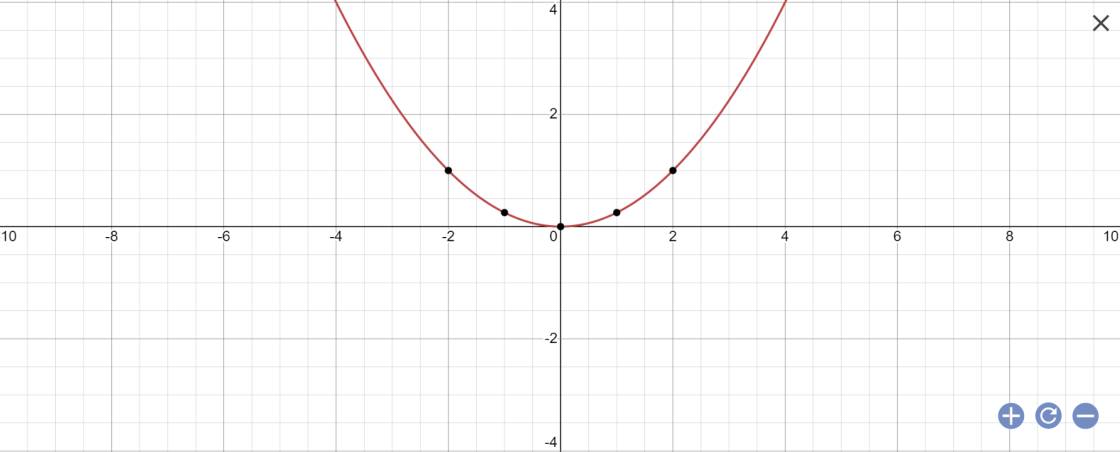
Đúng 0
Bình luận (0)
bài 1 : vẽ đồ thị hàm số của y = f(x) = 4x
a, tìm f(2) ,f(-2),f(4),f(0)
b,giá trị của x khi y = -1,y =0 , y=2,5
bài 2 : cho hàm số y = -3x
a, vẽ đồ thị hàm số trên
b, các diểm M (-2 và 6) có thuộc đồ thị hàm số trên không
c, xác định tọa độ của điểm P nằm trên đồ thị biết tung độ của P là 5
Bài 1 :
Với x = 1 thì y = 4.1 = 4
Ta được \(A\left(1;4\right)\) thuộc đồ thị hàm số y = f(x) = 4x
Đường thẳng OA là đồ thị hàm số y = f(x) = 4x
a) Ta có : \(f\left(2\right)=4\cdot2=8\)
\(f\left(-2\right)=4\cdot\left(-2\right)=-8\)
\(f\left(4\right)=4\cdot4=16\)
\(f\left(0\right)=4\cdot0=0\)
b) +) y = -1 thì \(4x=-1\) => \(x=-\frac{1}{4}\)
+) y = 0 thì 4x = 0 => x = 0
+) y = 2,5 thì 4x = 2,5 => \(4x=\frac{5}{2}\)=> x = \(\frac{5}{8}\)
Bài 2 :
a) Vẽ tương tự như bài 1
b) Thay \(M\left(-2,6\right)\)vào đths y = -3x ta có :
y =(-3)(-2) = 6
=> Điểm M thuộc đths y = -3x
c) Thay tung độ của P là 5 vào đồ thị hàm số y = -3x ta có :
=> 5 = -3x => \(x=-\frac{5}{3}\)
Vậy tọa độ của điểm P là \(P\left(-\frac{5}{3};5\right)\)
Cho hàm số y=1/4x^2 Tìm hoành độ giao điểm của M thuộc đồ thị (P) biết M có tung độ bằng 25
Do tung độ của M bằng 25 nên hoành độ M thỏa mãn:
\(25=\dfrac{1}{4}x^2\Leftrightarrow x^2=100\Rightarrow\left[{}\begin{matrix}x=10\\x=-10\end{matrix}\right.\)
Đúng 0
Bình luận (1)
cho hàm số y=1/4x^2 có đồ thị là (p) và hàm số y=x+m có đồ thị là (d)
a) Vẽ đồ thị (p) của hàm số y=1/4x^2
b) Tìm giá trị của m để (d) tiếp xúc với (p). Tìm tọa độ tiếp điểm
a) vẽ bạn tự vẽ nha
b) Xét pt hoành độ giao điểm chung của (d) và (P) ta có:
\(\frac{1}{4}x^2=x+m\)
\(\Leftrightarrow x^2-4x-4m=0\left(1\right)\)
\(\Delta^,=4+4m\)
Để (d) tiếp xúc với (P) \(\Leftrightarrow\Delta^,=0\)
\(\Leftrightarrow4+4m=0\)
\(\Leftrightarrow m=-1\)
Thay m=-1 vào pt (1) ta được :
\(x^2-4x+4=0\)
\(\Leftrightarrow\left(x-2\right)^2=0\)
\(\Leftrightarrow x=2\)
\(\Rightarrow y=\frac{1}{4}.2^2=1\)
Gọi tọa độ tiếp điểm của (d) tiếp xúc với (P) là A(x,y)
=> tọa độ tiếp điểm là \(A\left(2;1\right)\)
cho yX2_4x+1 a/ khảo sát và vẽ đồ thị b/ tìm tọa độ giao ddiemr giữa P và dcos y2x-4. tính độ dài độ dài MN...
Đọc tiếp
cho y=X2_4x+1 a/ khảo sát và vẽ đồ thị b/ tìm tọa độ giao ddiemr giữa P và dcos y=2x-4. tính độ dài độ dài MN c/tìm hàm số bậc hai mx2+nx+k(m>0) , có đồ thị đi qua đỉnh P đồng thời cắt trục hoành tại hai điểm A,B phân biệt và cắt trục tung tại điểm C( 0;5) sao cho SABC=10
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}x^2-4x+1=2x-4\\y=2x-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^2-6x+5=0\\y=2x-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(x-1\right)\left(x-5\right)=0\\y=2x-4\end{matrix}\right.\)
\(\Leftrightarrow\left(x,y\right)\in\left\{\left(1;-2\right);\left(5;6\right)\right\}\)
c: Điểm M,N ở đâu vậy bạn?
Đúng 0
Bình luận (0)
Cho hàm số: y = x2 có đồ thị (P) và hàm số y = 4x + m có đồ thị (dm)
Vẽ đồ thị (P).Tìm tất cả các giái trị của m sao cho (dm) và (P) cắt nhau tại hai điểm phân biệt, trong đó tung độ của một trong hai giao điểm đó bằng 1.1, bạn tự vẽ nha
2, xét pt: \(x^2=4x+m\Leftrightarrow x^2-4x-m=0\)(1) ; \(\Delta=16-4.-m=16+16m\)
(dm) và (P) cắt nhau tại hai điểm phân biệt <=> pt có 2 nghiệm p.biệt <=> \(\Delta>0\Leftrightarrow16+16m>0\Leftrightarrow m>-1\)
th1: chọn tung độ của giao điểm 1 là 1 <=> y1=1<=> \(x1=\sqrt{y1}=\sqrt{1}=1\); \(x1=\frac{4+\sqrt{16\left(m+1\right)}}{2}=\frac{4\left(1+\sqrt{m+1}\right)}{2}=2+2\sqrt{m+1}\)
thay x=1 vào ta có: \(2+2\sqrt{m+1}=1\Leftrightarrow2\sqrt{m+1}=-1\Rightarrow\)PTVN
th2: y2=1 <=> x2=1
\(x2=\frac{4-\sqrt{16\left(m+1\right)}}{2}=2-2\sqrt{m+1}\). thay x2=1 vào: \(2-2\sqrt{m+1}=1\Leftrightarrow-2\sqrt{m+1}=-1\Leftrightarrow\sqrt{m+1}=\frac{1}{2}\Leftrightarrow m+1=\frac{1}{4}\Leftrightarrow m=-\frac{3}{4}\)(t/m đk)
=> m=-3/4 thì (dm) và (P) cắt nhau tại hai điểm phân biệt, trong đó tung độ của một trong hai giao điểm đó bằng 1.
Đúng 0
Bình luận (0)
16-4(-m)=16+16m ??:D??
Viết pt tiếp tuyến của đồ thị hàm số \(y=2x^4-4x^2+1\) biết tung độ tiếp điểm bằng 1?
\(y'=8x^3-8x\)
\(y=3\Rightarrow2x^4-4x^2+1=1\Rightarrow\left[{}\begin{matrix}x=0\Rightarrow y'=0\\x=\sqrt{2}\Rightarrow y'=8\sqrt{2}\\x=-\sqrt{2}\Rightarrow y'=-8\sqrt{2}\end{matrix}\right.\)
Có 3 tiếp tuyến thỏa mãn: \(\left[{}\begin{matrix}y=1\\y=8\sqrt{2}\left(x-\sqrt{2}\right)+1\\y=-8\sqrt{2}\left(x+\sqrt{2}\right)+1\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Tìm tọa độ điểm A biết đồ thị hàm số y=4x qua A, hoành độ và tung độ của điểm A là 2 số nghịch đảo lẫn nhau.
Xác định hàm số bậc nhất y ax + b trong các trường hợpa) a -2 và đồ thị cắt trục hoành tại điểm có hoành độ 2,5b) a 3 và đồ thị cắt trục tung tại điểm có tung độ -dfrac{4}{3}c) đồ thị hàm số song song với đường thẳng y -4x + 3 và đi qua điểm A(-1;8)d) đồ thị hàm số đi qua điểm B (2;3) và cắt trục tung tại điểm có tung độ là 4e) đồ thị hàm số cắt trục tung tại điểm có tung độ là -2 và cắt đồ thị hàm số y -4x +3 tại điểm có hoành độ là 1f) đồ thị hàm số có hệ số góc là 2 và cắt đồ thị hàm số...
Đọc tiếp
Xác định hàm số bậc nhất y = ax + b trong các trường hợp
a) a = -2 và đồ thị cắt trục hoành tại điểm có hoành độ 2,5
b) a = 3 và đồ thị cắt trục tung tại điểm có tung độ -\(\dfrac{4}{3}\)
c) đồ thị hàm số song song với đường thẳng y = -4x + 3 và đi qua điểm A(-1;8)
d) đồ thị hàm số đi qua điểm B (2;3) và cắt trục tung tại điểm có tung độ là 4
e) đồ thị hàm số cắt trục tung tại điểm có tung độ là -2 và cắt đồ thị hàm số y = -4x +3 tại điểm có hoành độ là 1
f) đồ thị hàm số có hệ số góc là 2 và cắt đồ thị hàm số y = -4x + 3 tại điểm có tung độ là -3
a: a=-2 nên y=-2x+b
Thay x=2,5 và y=0 vào y=-2x+b, ta được:
\(b-2\cdot2,5=0\)
=>b-5=0
=>b=5
Vậy: y=-2x+5
b: a=3 nên y=3x+b
Thay x=0 và y=-4/3 vào y=3x+b, ta được:
\(b+3\cdot0=-\dfrac{4}{3}\)
=>\(b=-\dfrac{4}{3}\)
Vậy: \(y=3x-\dfrac{4}{3}\)
c: Vì đồ thị hàm số y=ax+b song song với đường thẳng y=-4x+3 nên \(\left\{{}\begin{matrix}a=-4\\b\ne3\end{matrix}\right.\)
Vậy: y=-4x+b
Thay x=-1 và y=8 vào y=-4x+b, ta được:
\(b-4\cdot\left(-1\right)=8\)
=>b+4=8
=>b=4
vậy: y=-4x+4
d: Thay x=0 và y=4 vào y=ax+b, ta được:
\(a\cdot0+b=4\)
=>b=4
Vậy: y=ax+4
Thay x=2 và y=3 vào y=ax+4, ta được:
\(a\cdot2+4=3\)
=>2a=3-4=-1
=>\(a=-\dfrac{1}{2}\)
Vậy: \(y=-\dfrac{1}{2}x+4\)
e: Thay x=0 và y=-2 vào y=ax+b, ta được:
\(a\cdot0+b=-2\)
=>b=-2
=>y=ax-2
Thay x=1 vào y=-4x+3, ta được:
\(y=-4\cdot1+3=-4+3=-1\)
Thay x=1 và y=-1 vào y=ax-2, ta được:
\(a\cdot1-2=-1\)
=>a-2=-1
=>a=1
Vậy: y=x-2
Đúng 1
Bình luận (0)




















