Cho hàm số f x = 7 − 4 x 2 k h i 0 ≤ x ≤ 1 4 − x 2 k h i x > 1 . Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số f x và các đường thẳng x = 0 , x = 3 , y = 0
A. 16 3
B. 20 3
C. 10
D. 9
Cho hàm số f(x) có f'(x) = (x2 - 4)(x3 - 1)2(3x - 27)(x - 25)3(x - 7)7. Số điểm cực đại của hàm số f(\(\left|x\right|\)) là?
Bài này khá dễ, chỉ cần tìm số nghiệm bội lẻ và dương của \(f'\left(x\right)=0\), gọi nó là k thì số cực trị của \(f\left(\left|x\right|\right)=2k+1\) (do đồ thị đối xứng qua Oy đồng thời luôn nhận \(x=0\) là 1 cực trị)
\(f'\left(x\right)=0\) có các nghiệm bội lẻ dương là 2; 3; 7; 25 tổng cộng 4 nghiệm
Do đó \(f\left(\left|x\right|\right)\) có 9 cực trị
Cho các Hàm số f1(x) = 5x2; f2(x) = -6x; f3(x) = 7/x; f4(x) = x5; f5(x) = x6 + x4. Trong các hàm số trên, hàm số nào có tính chất f(x) = f(-x) với mọi x?
Cho hàm số f(x) liên tục trên ℝ và có một nguyên hàm là F(x). Biết F(2) = –7. Giá trị của F(4) là:
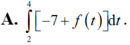
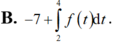
![]()
![]()
1.Cho hàm số y = g(x) = x - 4. Khi đó g(-2) bằng
A.-2 B.2 C.-6 D.6
2.Cho hàm số y = f(x) = -3x+ 5. Nếu f(x) = -7 thì x bằng
A.2/3 B.-4 C.2 D.4
Cho hàm số f(x) có f ( x ) = ( x + 1 ) 4 ( x - 2 ) 3 ( 2 x + 3 ) 7 ( x - 1 ) 10 . Tìm cực trị f(x)
A. 3
B. 2
C. 1
D. 4
Chọn B.
Xét :
![]()
Có nghiệm bội chẵn x = - 1 , x = 1 nên dấu của f’(x) qua hai nghiệm này không đổi dấu => x = 1 và x = - 1 không là cực trị
Có nghiệm bội lẻ x = 2 , x = - 3 2 , nên nó là hai cực trị
Kết luận: Hàm số có hai cực trị.
Cho hàm số y=f =-4x+3 Giá trị của hàm số khi x = 2x là A)f=-4 B)f=-5 C)f=-6 D)f=-7
Bài 2. Cho hàm số y = f (x) = |x - 4| + 7.
a) Tìm f(-1), f(3), f(4);
b) Tính các giá trị của x với f(x) = 5, f(x) = 7, f(x) = 8
Cho hàm số y=f(x)=3X
a, Vẽ đồ thị hàm số
b, Tính f(5); f(-7/12)
c, Các điểm M( -2:6), C( 4/9; 4/3) có thuộc đồ thị hàm số không ? Vì sao
Cho hàm số \(f \left(x\right)=2^{3-\frac{x}{4}}-7\)
a) Tính f(2)
b) Tính f(4)
c) Vẽ đồ thị của hàm số.