Phương pháp:
Công thức tính diện tích hình phẳng được giới hạn bởi các đường thẳng

Phương pháp:
Công thức tính diện tích hình phẳng được giới hạn bởi các đường thẳng

Cho hàm số f(x) thỏa mãn f ' x 2 + f x . f " x = 2018 x ∀ x ∈ R và f(0) = f’(0) = 1. Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số f(x), trục hoành và hai đường thẳng x = 0; x = 2. Tính thể tích V của khối tròn xoay tạo thành khi quay (H) quanh trục Ox.
A. V = 8090 3 2
B. V = 4036π
C. V = 8090 3 π
D. V = 8090π/3
Cho hàm số f(x) thỏa mãn f ' x 2 + f x f ' ' x = 2018 x , ∀ x ∈ ℝ và f 0 = f ' 0 = 1 . Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số f(x), trục hoành và hai đường thẳng x = 0 , x = 2 . Tính thể tích V của khối tròn xoay tạo thành khi quay (H) quanh trục Ox.
A. V = 8090 3 2 π
B. V = 4036 π
C. V = 8090 3 π
D. V = 8090 3 π
Cho hàm số f(x) luôn dương và có đạo hàm liên tục trên đoạn [1;4]. Biết rằng f ' ( x ) = e x f ( x ) , ∀ x∈ [1;4] và f(1)=1. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y=f' (x)=1, trục hoành và hai đường thẳng x=1,x=4.
A. e e 2 + 1 .
B. e 2 e 2 + 1 .
C. e 2 e 2 + 2 .
D. e e 2 + 2 .
Cho hàm số y = f ( x ) liên tục trên đoạn [a;b] có đồ thị như hình bên và c ∈ a ; b . Gọi S là diện tích của hình phẳng (H) giới hạn bởi đồ thị hàm số y = f ( x ) và các đường thẳng y = 0 , x = a , x = b . . Mệnh đề nào sau đây sai?
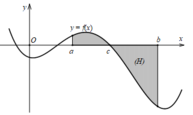
A. S = ∫ a c f x d x + ∫ c b f x d x
B. S = ∫ a c f x d x − ∫ c b f x d x
C. S = ∫ a b f x d x
D. S = ∫ a c f x d x + ∫ b c f x d x
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f ( x ) = sinx cosx , đường thẳng y = 0 , x = 0 và x = π 2 .
A. 1 2
B. 1
C. 1 4
D. π 2
Cho hàm số y = f(x) liên tục trên [a;b]. Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x=a, x=b được tình theo công thức.
A. S = π ∫ a b f x 2 d x .
B. S = ∫ a b f x d x .
C. S = π ∫ a b f x d x .
D. S = ∫ a b f x d x .
Cho hình phẳng (H) giới hạn bởi đồ thị hàm số y = x − 1 x + 2 và các đường thẳng Δ : y = 2 , d : − 2 x − 4 (tham khảo hình bên). Tính diện tích hình phẳng (H)
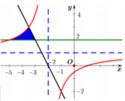
A. 1 4 + 3 ln 2
B. 1 4
C. − 2 + 3 ln 3
D. − 5 4 + 3 ln 2
Tính diện tích S của miền hình phẳng giới hạn bởi đồ thị của hàm số f ( x ) = a x 3 + b x 2 + c , các đường thẳng x = - 1 , x = 2 và trục hoành (miền tô đậm) cho trong hình dưới đây
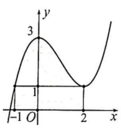
A. S = 51 8
B. S = 52 8
C. S = 50 8
D. S = 53 8
Cho hàm số y = f ( x ) = 3 x 2 khi x ≤ 1 4 - x khi > 1 . Thể tích của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số y = f(x) trục hoành và các đường thẳng x = 0, x = 2 quanh trục hoành bằng
A. 29 4
B. 29 π 4
C. 122 15
D. 122 π 15