Các câu hỏi tương tự
Cho hàm số f(x) liên tục trên
ℝ
và F(x) là nguyên hàm của f(x), biết
∫
0
9
f
x
d
x
9
và F(0) 3. Giá trị của F(9) bằng A. F(9) 6 B. F(9) 12 C. F(9) –6 D. F(9) –12
Đọc tiếp
Cho hàm số f(x) liên tục trên ℝ và F(x) là nguyên hàm của f(x), biết ∫ 0 9 f x d x = 9 và F(0) = 3. Giá trị của F(9) bằng
A. F(9) = 6
B. F(9) = 12
C. F(9) = –6
D. F(9) = –12
Cho hàm số yf(x) có đạo hàm liên tục trên
ℝ
và có một nguyên hàm là hàm số
y
1
2
x
2
-
x
+
1
.
Giá trị của biểu thức
∫
1
2
f
(
x
2
)
d
x
bằng A.
-
4
3...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm liên tục trên ℝ và có một nguyên hàm là hàm số y = 1 2 x 2 - x + 1 . Giá trị của biểu thức ∫ 1 2 f ( x 2 ) d x bằng
A. - 4 3
B. 4 3
C. - 2 3
D. 2 3
Cho hàm số f(x) liên tục trên
ℝ
và F(x) là nguyên hàm của f(x), biết
∫
0
9
f
(
x
)
d
x
9
, F(0)3. Tính F(9). A. -6. B. 6. C. 12. D. -12.
Đọc tiếp
Cho hàm số f(x) liên tục trên ℝ và F(x) là nguyên hàm của f(x), biết ∫ 0 9 f ( x ) d x = 9 , F(0)=3. Tính F(9).
A. -6.
B. 6.
C. 12.
D. -12.
Cho hàm số yf(x) có đạo hàm liên tục trên
ℝ
thỏa mãn f(x) -xf(x) 0,
f
x
0
,
∀
x
∈
ℝ
và f(0) 1. Giá trị của f(1) bằng? A.
1
e
. B.
1
e
.
C.
e
.
D. e.
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm liên tục trên ℝ thỏa mãn f'(x) -xf(x) = 0, f x > 0 , ∀ x ∈ ℝ và f(0) = 1. Giá trị của f(1) bằng?
A. 1 e .
B. 1 e .
C. e .
D. e.
Cho hàm số f(x) có đạo hàm liên tục trên
ℝ
và thỏa mãn f(x) 0,
∀
x
∈
ℝ
. Biết f(0) 1 và
f
(
x
)
(
6
x
-
3
x
2
)
f
(
x
)
.
Tìm tất cả các giá trị thực của tham số m để phương trình f(x) m có ngh...
Đọc tiếp
Cho hàm số f(x) có đạo hàm liên tục trên ℝ và thỏa mãn f(x) > 0, ∀ x ∈ ℝ . Biết f(0) = 1 và f ' ( x ) = ( 6 x - 3 x 2 ) f ( x ) . Tìm tất cả các giá trị thực của tham số m để phương trình f(x) = m có nghiệm duy nhất.
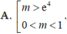
![]()
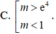
![]()
Cho hàm số y f(x) liên tục trên
ℝ
sao cho
m
a
x
x
∈
[
0
;
10
]
f
(
x
)
f(2) 4. Xét hàm số g(x)
f
x
3
+
x
-...
Đọc tiếp
Cho hàm số y = f(x) liên tục trên ℝ sao cho m a x x ∈ [ 0 ; 10 ] f ( x ) = f(2) = 4. Xét hàm số g(x) = f x 3 + x - x 2 + 2 x + m . Giá trị của tham số m để m a x x ∈ [ 0 ; 2 ] g ( x ) = 8 là
A. 5
B. 4
C. -1
D. 3
Cho hàm số y f(x) , có đạo hàm là f(x) liên tục trên
ℝ
và hàm số f(x) có đồ thị như hình dưới đây. Hỏi hàm số y f(x) có bao nhiêu cực trị? A. 1. B. 0. C. 3. D. 2.
Đọc tiếp
Cho hàm số y = f(x) , có đạo hàm là f'(x) liên tục trên ℝ và hàm số f'(x) có đồ thị như hình dưới đây.
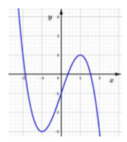
Hỏi hàm số y = f(x) có bao nhiêu cực trị?
A. 1.
B. 0.
C. 3.
D. 2.
Hàm số
y
f
(
x
)
xác định và liên tục trên R có đạo hàm
f
(
x
)
x
-
1
3
x
-
2
2
x
3
,
∀
x...
Đọc tiếp
Hàm số y = f ( x ) xác định và liên tục trên R có đạo hàm f ' ( x ) = x - 1 3 x - 2 2 x 3 , ∀ x ∈ ℝ . Số điểm cực trị của hàm số y = f ( x ) là
A. 3
B. 1
C. 0
D. 2
Cho hàm số f(x) có f(x) và f(x) liên tục trên
ℝ
. Biết f(2)4 và f(-1) -2. Tính
∫
-
1
2
f
(
x
)
d
x
A. -8. B. -6. C. 2. D. 6.
Đọc tiếp
Cho hàm số f(x) có f'(x) và f"(x) liên tục trên ℝ . Biết f'(2)=4 và f'(-1)= -2. Tính ∫ - 1 2 f " ( x ) d x
A. -8.
B. -6.
C. 2.
D. 6.