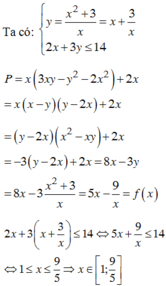Nếu x + y = 0 thì giá trị của biểu thức A = x3 + 2x2y + 2x + xy2 + 2y + 12 = ...

Những câu hỏi liên quan
1,phân tích mỗi đa thức sau thành phân tử
a,(x+2y)2-(x-y)2
b,(x+1)3+(x-1)3
c,9x2-3x+2y-4y2
d,4x2-4xy+2x-y+y2
e,x3+3x2+3x+1-y3
g,x3-2x2y+xy2-4x
a) \(\left(x+2y\right)^2-\left(x-y\right)^2=\left(x+2y+x-y\right)\left(x+2y-x+y\right)\)
\(=\left(2x+y\right).3y\)
b) \(\left(x+1\right)^3+\left(x-1\right)^3\)
\(=\left(x+1+x-1\right)\left[\left(x+1\right)^2-\left(x+1\right)\left(x-1\right)+\left(x-1\right)^2\right]\)
\(=2x\left[\left(x+1\right)^2-\left(x^2-1\right)+\left(x-1\right)^2\right]\)
c) \(9x^2-3x+2y-4y^2\)
\(=9x^2-4y^2-3x+2y\)
\(=\left(3x-2y\right)\left(3x+2y\right)-\left(3x-2y\right)\)
\(=\left(3x-2y\right)\left[3x+2y-1\right]\)
d) \(4x^2-4xy+2x-y+y^2\)
\(=4x^2-4xy+y^2+2x-y\)
\(=\left(2x-y\right)^2+2x-y\)
\(=\left(2x-y\right)\left(2x-y+1\right)\)
e) \(x^3+3x^2+3x+1-y^3\)
\(=\left(x+1\right)^3-y^3\)
\(=\left(x+1-y\right)\left[\left(x+1\right)^2+y\left(x+1\right)+y^2\right]\)
g) \(x^3-2x^2y+xy^2-4x\)
\(=x\left(x^2-2xy+y^2\right)-4x\)
\(=x\left(x-y\right)^2-4x\)
\(=x\left[\left(x-y\right)^2-4\right]\)
\(=x\left(x-y+2\right)\left(x-y-2\right)\)
Đúng 1
Bình luận (0)
a) (x + 2y)² - (x - y)²
= (x + 2y - x + y)(x + 2y + x - y)
= 3y(2x + y)
b) (x + 1)³ + (x - 1)³
= (x + 1 + x - 1)[(x + 1)² - (x + 1)(x - 1) + (x - 1)²]
= 2x(x² + 2x + 1 - x² + 1 + x² - 2x + 1)
= 2x(x² + 3)
c) 9x² - 3x + 2y - 4y²
= (9x² - 4y²) - (3x - 2y)
= (3x - 2y)(3x + 2y) - (3x - 2y)
= (3x - 2y)(3x + 2y - 1)
d) 4x² - 4xy + 2x - y + y²
= (4x² - 4xy + y²) + (2x - y)
= (2x - y)² + (2x - y)
= (2x - y)(2x - y + 1)
e) x³ + 3x² + 3x + 1 - y³
= (x³ + 3x² + 3x + 1) - y³
= (x + 1)³ - y³
= (x + 1 - y)[(x + 1)² + (x + 1)y + y²]
= (x - y + 1)(x² + 2x + 1 + xy + y + y²)
g) x³ - 2x²y + xy² - 4x
= x(x² - 2xy + y² - 4)
= x[(x² - 2xy + y²) - 4]
= x[(x - y)² - 2²]
= x(x - y - 2)(x - y + 2)
Đúng 1
Bình luận (0)
Phân tích các đa thức sau thành nhân tử:a/ 2x3 + 3x2 + 2x +3 b/ x2 – x – 12 c/ 4x2 –( x2 + 1)2d/ 4xy2 – 12x2y + 8xy e/ x2 + x – 6 f/ x3 + 2x2y + xy2 – 4xz2g/ x3 – 2x2y + xy2 – 25x h/ x2 – 2x – 3 i/ x3 – 3x2 – 9x + 27
Đọc tiếp
Phân tích các đa thức sau thành nhân tử:
a/ 2x3 + 3x2 + 2x +3 b/ x2 – x – 12 c/ 4x2 –( x2 + 1)2
d/ 4xy2 – 12x2y + 8xy e/ x2 + x – 6 f/ x3 + 2x2y + xy2 – 4xz2
g/ x3 – 2x2y + xy2 – 25x h/ x2 – 2x – 3 i/ x3 – 3x2 – 9x + 27
a: \(=x^2\left(2x+3\right)+\left(2x+3\right)\)
\(=\left(2x+3\right)\left(x^2+1\right)\)
b: \(=\left(x-4\right)\left(x+3\right)\)
e: =(x+3)(x-2)
Đúng 1
Bình luận (0)
a) \(=x^2\left(2x+3\right)+\left(2x+3\right)=\left(2x+3\right)\left(x^2+1\right)\)
b) \(=x\left(x-4\right)+3\left(x-4\right)=\left(x-4\right)\left(x+3\right)\)
c) \(=\left(2x\right)^2-\left(x^2+1\right)^2=\left(x^2-2x+1\right)\left(x^2+2x+1\right)=\left(x-1\right)^2\left(x+1\right)^2\)
d) \(=4xy\left(y-3x+2\right)\)
e) \(=x\left(x-2\right)+3\left(x-2\right)=\left(x-2\right)\left(x+3\right)\)
f) \(=x\left(x^2+2xy+y^2-4z^2\right)=x\left[\left(x+y\right)^2-4z^2\right]=x\left(x+y-2z\right)\left(x+y+2z\right)\)
g) \(=x\left(x^2-2xy+y^2-25\right)=x\left[\left(x-y\right)^2-25\right]=x\left(x-y-5\right)\left(x-y+5\right)\)
h) \(=x\left(x+1\right)-3\left(x+1\right)=\left(x+1\right)\left(x-3\right)\)
i) \(=x^2\left(x-3\right)-9\left(x-3\right)=\left(x-3\right)\left(x^2-9\right)=\left(x-3\right)^2\left(x+3\right)\)
Đúng 1
Bình luận (0)
Câu 11. Giá trị của biểu thức - 2x2 + xy2 tại x -1 ; y - 4 là:A. - 2 B. - 18 C. 3 D. 1Câu 12: 2. Thu gọn đa thức P -2x2y – 7xy2 + 3x2y + 7xy2 được kết quả.A. P -5x2y - 14 xy2 B. P x2y C. P x2y + 14 xy2 D. P -x2y Câu 13: Tam giác nào là tam giác vuông trong các tam giác có độ dài ba cạnh là:A. 5; 5; 7 B. ...
Đọc tiếp
Câu 11. Giá trị của biểu thức - 2x2 + xy2 tại x= -1 ; y = - 4 là:
A. - 2 B. - 18 C. 3 D. 1
Câu 12: 2. Thu gọn đa thức P = -2x2y – 7xy2 + 3x2y + 7xy2 được kết quả.
A. P = -5x2y - 14 xy2 B. P = x2y C. P = x2y + 14 xy2 D. P = -x2y
Câu 13: Tam giác nào là tam giác vuông trong các tam giác có độ dài ba cạnh là:
A. 5; 5; 7 B. 4; 5; 6 C. 10; 8; 6 D. 2; 3; 4
Câu 14: ABC và DEF có AB = ED, BC = EF. Thêm điều kiện nào sau đây để ABC= DEF?
A. = B. = C. AB = AC D. AC = DF
Câu 15: MNP cân tại P. Biết góc N có số đo bằng 500. Số đo góc P bằng:
A. 800 B. 1000 C. 500 D. 1300
Câu 16: HIK vuông tại H có các cạnh góc vuông là 3cm; 4cm. Độ dài cạnh huyền IK bằng
A. 8cm B. 16cm C.5cm D. 12cm
Câu 17: Cho tam giác ABC bằng tam giác DEF, góc tương ứng với góc C là
A. Góc D B. Góc F C. Góc E D. Góc B
Câu 18: Cho tam giác ABC vuông tại A. Ta có:
A. = - B. + = 900
C. Hai góc B và C kề bù. D. Hai góc B và C bù nhau
Câu 19: Tìm x trong hình vẽ sau biết AB // CD
A. 600 B. 700 C. 500 D. 800
Câu 20: Tìm tam giác cân trong hình dưới đây:
A. ABE B. CAD
C. CAB và EAD D. Không có tam giác cân nào trong hình vẽ trên.
Câu 11. Giá trị của biểu thức - 2x2 + xy2 tại x= -1 ; y = - 4 là:
A. - 2 B. - 18 C. 3 D. 1
Câu 12: 2. Thu gọn đa thức P = -2x2y – 7xy2 + 3x2y + 7xy2 được kết quả.
A. P = -5x2y - 14 xy2 B. P = x2y C. P = x2y + 14 xy2 D. P = -x2y
Câu 13: Tam giác nào là tam giác vuông trong các tam giác có độ dài ba cạnh là:
A. 5; 5; 7 B. 4; 5; 6 C. 10; 8; 6 D. 2; 3; 4
Câu 14: ABC và DEF có AB = ED, BC = EF. Thêm điều kiện nào sau đây để ABC= DEF?
A. = B. = C. AB = AC D. AC = DF
Câu 15: MNP cân tại P. Biết góc N có số đo bằng 500. Số đo góc P bằng:
A. 800 B. 1000 C. 500 D. 1300
Câu 16: HIK vuông tại H có các cạnh góc vuông là 3cm; 4cm. Độ dài cạnh huyền IK bằng
A. 8cm B. 16cm C.5cm D. 12cm
Câu 17: Cho tam giác ABC bằng tam giác DEF, góc tương ứng với góc C là
A. Góc D B. Góc F C. Góc E D. Góc B
Câu 18: Cho tam giác ABC vuông tại A. Ta có:
A. = - B. + = 900
C. Hai góc B và C kề bù. D. Hai góc B và C bù nhau
Câu 19: Tìm x trong hình vẽ sau biết AB // CD
A. 600 B. 700 C. 500 D. 800
Câu 20: Tìm tam giác cân trong hình dưới đây:
A. ABE B. CAD
C. CAB và EAD D. Không có tam giác cân nào trong hình vẽ trên.
Đúng 1
Bình luận (0)
Cho x,y 0 và thỏa mãn
x
2
-
x
y
+
3
0
2
x
+
2
y
-...
Đọc tiếp
Cho x,y > 0 và thỏa mãn x 2 - x y + 3 = 0 2 x + 2 y - 14 ≤ 0 .Tính tổng giá trị lớn nhất và nhỏ nhất của biểu thức P = 3 x 2 y - x y 2 - 2 x 3 + 2 x
A. 4.
B. 8.
C. 12.
D. 0.
A=x3 + x2y-xy2-y3+x2-y2+2x+2x+3
Tìm giá trị của đa thức A biết x+y= -1
Sửa đề: \(A=x^3+x^2y-xy^2-y^3+x^2-y^2+2x+2y+3\)
\(A=x^2\left(x+y\right)-y^2\left(x+y\right)+\left(x-y\right)\left(x+y\right)+2x+2y+3\)
\(=-x^2+y^2+\left(-x+y\right)-2+3\)
\(=-\left(x-y\right)\left(x+y\right)-\left(x-y\right)+1\)
\(=\left(x-y\right)\left(-x-y-1\right)+1\)
\(=\left(x-y\right)\left(1-1\right)+1=1\)
Đúng 0
Bình luận (0)
Phân tích đa thức thành nhân tử:
+)5x2y2+15x2+30xy2
+)(x-2)(x-3)+4-x2
+)x2-7x+12
+)x3-2x2y+xy2-9x
+)x2-25+y2+2xy
+)x2-x-12
+)5x25xy-x-y
+)12y(2x-5)+6xy(5-2x)
+)16x2+24x-8xy-6y+y2
+)(x+3)(x+6)(x+9)(x+12)+81
a: \(=5x\left(xy^2+3x+6y^2\right)\)
b: \(=\left(x-2\right)\left(x+3\right)-\left(x-2\right)\left(x+2\right)=\left(x-2\right)\left(x+3-x-2\right)=\left(x-2\right)\)
c: \(=\left(x-3\right)\left(x-4\right)\)
d: \(=x\left(x^2-2xy+y^2-9\right)\)
=x(x-y-3)(x-y+3)
e: \(=\left(x+y\right)^2-25=\left(x+y+5\right)\left(x+y-5\right)\)
f: \(=\left(x-4\right)\left(x+3\right)\)
Đúng 0
Bình luận (0)
tính giá trị của đa thức sau, biet x+y-2=0
A=x3-2x2-xy2+2xy+2y+2x-2
Tính giá trị của các biểu thức: x3 + x2y + xy2 + 2xy(x + y)
biết x + y = 2
Đề sai r bn, nếu x,y thay đổi thì tổng biểu thức cũng thay đổi
Đúng 0
Bình luận (0)
Giá trị của biểu thức D
x
3
–
x
2
y
–
x
y
2
+
y
3
khi x y là A. 3 B. 2 C. 1 D. 0
Đọc tiếp
Giá trị của biểu thức D = x 3 – x 2 y – x y 2 + y 3 khi x = y là
A. 3
B. 2
C. 1
D. 0
D = ( x 3 + y 3 ) – x y ( x + y ) = ( x + y ) ( x 2 – x y + y 2 ) – x y ( x + y ) = ( x + y ) ( x 2 – x y + y 2 – x y ) = ( x + y ) [ x ( x – y ) – y ( x – y ) ] = ( x + y ) ( x – y ) 2
Vì x = y ó x – y = 0 nên D = ( x + y ) ( x – y ) 2 = 0
Đáp án cần chọn là: D
Đúng 0
Bình luận (0)
Phân tích thành nhân tử
1)(2x+y)2-4y2
2)64-125x3
3)x3-2x2y+xy2-4x
4)x3-y3+x2y-xy2
1: =(2x+y-2y)(2x+y+2y)
=(2x-y)(2x+3y)
2: =(4-5x)(16+20x+25x^2)
3: =x(x^2-2xy+y^2-4)
=x[(x-y)^2-4]
=x(x-y-2)(x-y+2)
4: =(x-y)(x^2+xy+y^2)+xy(x-y)
=(x-y)(x^2+2xy+y^2)
=(x-y)(x+y)^2
Đúng 4
Bình luận (0)
1: =(2x+y-2y)(2x+y+2y)
=(2x-y)(2x+3y)
2: =(4-5x)(16+20x+25x^2)
3: =x(x^2-2xy+y^2-4)
=x[(x-y)^2-4]
=x(x-y-2)(x-y+2)
4: =(x-y)(x^2+xy+y^2)+xy(x-y)
=(x-y)(x^2+2xy+y^2)
=(x-y)(x+y)^2
Đúng 1
Bình luận (0)