Hàm số y = 25 - x 2 nghịch biến trên khoảng:
A. (- ∞ ; 0) B. (-5; 0)
C. (0; 5) D. (5; + ∞ )
Câu 25. Cho hàm số \(y = \dfrac{x + 1}{x - 1}, y = -x^3+x^2-3x+1, y = x^4 + 2x^2 +2.\) Trong các hàm số trên, có bao nhiêu hàm số đơn điệu trên \(R\)?
A. 1. B. 3. C. 0. D. 2.
\(y'_1=-\dfrac{2}{\left(x-1\right)^2}\) nghịch biến trên R/{1}
\(y'_2=-3x^2+2x-3\) có nghiệm khi y' = 0
\(y'_3=4x^3+4x\) có nghiệm khi y' = 0
Vậy không có hàm số đơn điệu trên R.
Tìm các hàm số bậc nhất trong các hàm số sau đây và chỉ ra các hệ số \(a,b\) của các hàm số đó:
\(y = 4x - 7\);\(y = {x^2}\);\(y = - 6x - 4\);\(y = 4x\);\(y = \dfrac{3}{x}\);\(s = 5v + 8\);\(m = 30n - 25\).
- Hàm số\(y = 4x - 7\) là hàm số bậc nhất vì hàm số có dạng \(y = ax + b\)với \(a,b\) là các số cho trước và \(a \ne 0\). Hệ số \(a = 4;b = - 7\).
- Hàm số \(y = {x^2}\) không là hàm số bậc nhất vì hàm số không có dạng \(y = ax + b\)với \(a,b\) là các số cho trước và \(a \ne 0\).
- Hàm số \(y = - 6x - 4\)là hàm số bậc nhất vì hàm số có dạng \(y = ax + b\)với \(a,b\) là các số cho trước và \(a \ne 0\). Hệ số \(a = - 6;b = - 4\).
- Hàm số \(y = 4x\)là hàm số bậc nhất vì hàm số có dạng \(y = ax + b\)với \(a,b\) là các số cho trước và \(a \ne 0\). Hệ số \(a = 4;b = 0\).
- Hàm số \(y = \dfrac{3}{x}\) không là hàm số bậc nhất vì hàm số không có dạng \(y = ax + b\)với \(a,b\) là các số cho trước và \(a \ne 0\).
- Hàm số \(s = 5v + 8\) là hàm số bậc nhất vì hàm số có dạng \(s = av + b\)với \(a,b\) là các số cho trước và \(a \ne 0\). Hệ số \(a = 5;b = 8\).
- Hàm số \(m = 30n - 25\) là hàm số bậc nhất vì hàm số có dạng \(m = an + b\)với \(a,b\) là các số cho trước và \(a \ne 0\). Hệ số \(a = 30;b = - 25\).
Cho hàm số y = ( 5 m + 2 ) x 2 v ớ i m ≠ - 2 5 . Tìm m để hàm số nghịch biến với mọi x > 0
A. m < - 2 5
B. m > 2 5
C. m < 2 5
D. m > - 2 5
Để hàm số nghịch biến với mọi x > 0 thì a < 0 nên 5m + 2 < 0 ⇔ m < − 2 5
Vậy m < − 2 5 thỏa mãn điều kiện đề bài
Đáp án cần chọn là: A
Vẽ đồ thị hàm số:
1, y = 1/4x mũ 2
2, y = -1/4 x mũ 2
3, y = -2 x mũ 2
4, y = -1/2 x mũ 2
5, y = 3 x mũ 2
Tìm max của hàm số: \(y=\left(\dfrac{2x}{x^2+1}\right)^2-\dfrac{8x}{x^2+1}+25\)
Lời giải:
Đặt $t=\frac{2x}{x^2+1}$
$t+1=\frac{(x+1)^2}{x^2+1}\geq 0\Rightarrow t\geq -1$
$1-t=\frac{(x-1)^2}{x^2+1}\geq 0\Rightarrow t\leq 1$
Vậy $-1\leq t\leq 1$
$y=t^2-4t+25=(t+1)(t-5)+30$
Vì $-1\leq t\leq 1$ nên $t+1\geq 0; t-5\leq 0\Rightarrow (t+1)(t-5)\leq 0$
$\Rightarrow y\leq 30$
Vậy $y_{\max}=30$
Câu 24. Cho hàm số y = f (x) = -2x . Ta có :
A. f (0) = -2 B. f (1) = -2 C. f (-1) = -2 D. f(1) = 2
Câu 25. Điểm thuộc đồ thị hàm số y = - 2x là :
A. M ( - 1; -2 ) B. N ( 1; 2 ) C. P ( 0 ; -2 ) D. Q ( -1; 2 )
Câu 26. Đồ thị hàm số y = 2 x là :
A. Một đường cong B. Một đường cong đi qua gốc tọa độ
C. Một đường thẳng đi qua gốc tọa độ D. Một đường thẳng không đi qua gốc tọa độ
Câu 24: B
Câu 25: D
Câu 26: C
a) Xét tính liên tục của hàm số y = g ( x ) tại x 0 = 2 , biết: g x = x 3 - 8 x - 2 n ế u x ≠ 2 5 n ế u x = 2
b.Trong biểu thức g(x) ở trên, cần thay số 5 bởi số nào đó để hàm số liên tục tại x 0 = 2 .
a) Ta có: g(2) = 5.
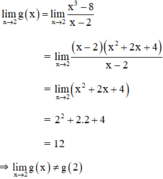
⇒ g(x) không liên tục tại x = 2.
b) Để g(x) liên tục tại x = 2
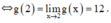
Vậy để hàm số liên tục tại x = 2 thì cần thay 5 bằng 12.
Quan sát đồ thị hàm số \(y = \sin x\) ở Hình 25.
a) Nêu tập giá trị của hàm số \(y = \sin x\)
b) Gốc tọa độ có là tâm đối xứng của đồ thị hàm số không? Từ đó kết luận tính chẵn, lẻ của hàm số \(y = \sin x\)
c) Bằng cách dịch chuyển đồ thị hàm số \(y = \sin x\) trên đoạn \(\left[ { - \pi ;\pi } \right]\) song song với trục hoành sang phải theo đoạn có độ dài \(2\pi \), ta có nhận được đồ thị hàm số \(y = \sin x\) trên đoạn \(\left[ {\pi ;3\pi } \right]\) hay không? Hàm số \(y = \sin x\)có tuần hoàn hay không/
d) Tìm khoảng đồng biến, nghịch biến của hàm số \(y = \sin x\)
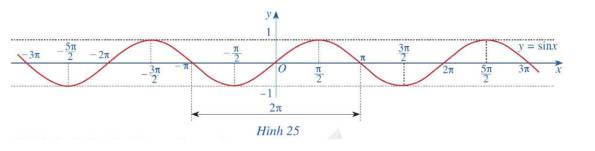
a) Tập giá trị của hàm số\(y = \sin x\) là \(\left[ { - 1;1} \right]\)
b) Đồ thị hàm số \(y = \sin x\) nhận O là tâm đối xứng.
Như vậy hàm số \(y = \sin x\) là hàm số lẻ.
c) Bằng cách dịch chuyển đồ thị hàm số \(y = \sin x\) trên đoạn \(\left[ { - \pi ;\pi } \right]\) song song với trục hoành sang phải theo đoạn có độ dài \(2\pi \), ta nhận được đồ thị hàm số \(y = \sin x\) trên đoạn \(\left[ {\pi ;3\pi } \right]\)
Như vậy, hàm số \(y = \sin x\) có tuần hoàn .
d) Hàm số \(y = \sin x\) đồng biến trên mỗi khoảng \(\left( { - \frac{\pi }{2} + k2\pi ;\frac{\pi }{2} + k2\pi } \right)\), nghịch biến trên mỗi khoảng \(\left( {\frac{\pi }{2} + k2\pi ;\frac{{3\pi }}{2} + k2\pi } \right)\) với \(k \in Z\)
Cho hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{\frac{{{x^2} - 25}}{{x - 5}}}&{khi\,\,x \ne 5}\\a&{khi\,\,x = 5}\end{array}} \right.\).
Tìm \(a\) để hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\).
Trên các khoảng \(\left( { - \infty ;5} \right)\) và \(\left( {5; + \infty } \right)\), \(f\left( x \right) = \frac{{{x^2} - 25}}{{x - 5}}\) là hàm phân thức hữu tỉ nên liên tục trên từng khoảng \(\left( { - \infty ;5} \right)\) và \(\left( {5; + \infty } \right)\).
Ta có: \(f\left( 5 \right) = a\)
\(\mathop {\lim }\limits_{x \to 5} f\left( x \right) = \mathop {\lim }\limits_{x \to 5} \frac{{{x^2} - 25}}{{x - 5}} = \mathop {\lim }\limits_{x \to 5} \frac{{\left( {x - 5} \right)\left( {x + 5} \right)}}{{x - 5}} = \mathop {\lim }\limits_{x \to 5} \left( {x + 5} \right) = 5 + 5 = 10\)
Để hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) thì hàm số \(y = f\left( x \right)\) phải liên tục tại điểm \({x_0} = 5\). Khi đó: \(\mathop {\lim }\limits_{x \to 5} f\left( x \right) = f\left( 5 \right) \Leftrightarrow a = 10\).
Vậy với \(a = 10\) thì hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\).
giúp mik vs ạ![]()
bài 1
a tìm số thực x biết: |x - 25/3| -2=7/3
b cho hàm số y=ʃ(x)= 3-\(^{2x^2}\) . tính ʃ(1/2)