a: Xét ΔAMN và ΔBMD có 

MA=MB

\(\widehat{AMN}=\widehat{BMD}\)

MN=MD

Do đó: ΔAMN=ΔBMD

b: Xét tứ giác ADBN có 

M là trung điểm của AB

M là trung điểm của DN

Do đó: ADBN là hình bình hành

Suy ra: DB//AN

hay DB//AC

Ta có hình vẽ:

a) Vì M là trung điểm của AB nên AM = BM = \(\frac{AB}{2}\)

Xét Δ AMK và Δ BMC có:

AM = BM (cmt)

AMK = BMC (đối đỉnh)

MK = MC (gt)

Do đó, Δ AMK = Δ BMC (c.g.c) (đpcm)

b) Vì N là trung điểm của AC nên AN = NC

Xét Δ ANI và Δ CNB có:

AN = NC (cmt)

ANI = CNB (đối đỉnh)

NI = NB (gt)

Do đó, Δ ANI = Δ CNB (c.g.c)

=> AI = BC (2 cạnh tương ứng) (đpcm)

c) Vì Δ AMK = Δ BMC (câu a) => AKM = MCB (2 góc tương ứng)

Mà AKM và MCB là 2 góc so le trong nên AK // BC (1)

Vì Δ ANI = Δ CNB (câu b) => IAN = NBC (2 góc tương ứng)

Mà IAN và NBC là 2 góc so le trong nên AI // BC (2)

Từ (1) và (2) => AK và AI trùng nhau hay 3 điểm I, A, K thẳng hàng (3)

Có: Δ AMK = Δ BMC (câu a) => AK = BC (2 cạnh tương ứng)

Mà AI = BC (câu b) => AK = AI (4)

Từ (3) và (4) => A là trung điểm của IK (đpcm)

2

ta có 

N là trung điểm của AC

M là trung điểm của AB

=> MN là đường trung bình  

=> MN // BC  và  =1/2BC      (1)

MN=NE=1/2BC    

=>MN+NE=1/2BC+1/2BC=BC   (2)

từ 1 và 2 =>MECB là hình bình hành (2 cặp đối // và bằng nhau)

Vì \(\left\{{}\begin{matrix}AM=MB\\AN=NC\end{matrix}\right.\) nên MN là đtb tam giác BAC

Do đó \(MN//BC\) hay \(ME//BC\)

Và \(2MN=BC=ME\left(E.là.trung.điểm\right)\)

Vậy MECB là hbh

a: Xét ΔABM và ΔACM có 

AB=AC

BM=CM

AM chung

Do đó: ΔABM=ΔACM

b: Xét tứ giác AMCE có 

N là trung điểm của AC

N là trung điểm của ME

Do đó: AMCE là hình bình hành

Suy ra: AE=CM

1) Xét tam giác MNH và tam giác MKH có:

+ MN = MK (gt).

+ MH chung.

+ NH = KH (H là trung điểm NK).

=> Tam giác MNH = Tam giác MKH (c - c - c).

3) Ta có: MD = MN + ND; ME = MK + KE.

Mà ND = KE (gt); MN = MK (gt).

=> MD = ME.

Xét tam giác MNK có: MN = MK (gt).

=> Tam giác MNK cân tại M.

Mà MH là đường trung tuyến (H là trung điểm NK).

=> MH là đường phân giác \(\widehat{M}\) (Tính chất các đường trong tam giác cân).

Xét tam giác HMD và tam giác HME:

+ MD = ME (cmt).

+ \(\widehat{DMH}=\widehat{EMH}\) (MH là đường phân giác \(\widehat{M}\)).

+ MH chung.

=> Tam giác HMD = Tam giác HME (c - g - c).

4) Xét tam giác MDE có: MD = ME (cmtt).

=> Tam giác MDE cân tại M.

Mà MO là đường trung tuyến (O là trung điểm DE).

=> MO là đường phân giác \(\widehat{M}\) (Tính chất các đường trong tam giác cân).

Mà MH là đường phân giác \(\widehat{M}\) (cmt).

=> Ba điểm M, H, O thẳng hàng.

5) Xét tam giác MDE cân tại M có: MO là đường trung tuyến (O là trung điểm DE).

=> MO là đường cao (Tính chất các đường trong tam giác cân).

=> MO \(\perp\) DE. (1)

Xét tam giác MNK cân tại M có: MH là đường trung tuyến (H là trung điểm NK).

=> MH là đường cao (Tính chất các đường trong tam giác cân).

=> MH \(\perp\) NK

Hay MO \(\perp\) NK. (2)

Từ (1) và (2) => NK // DE (Từ vuông góc đến song song).

a: Xét ΔDEM và ΔDFM có

DE=DF

DM chung

EM=FM

Do đó: ΔDEM=ΔDFM

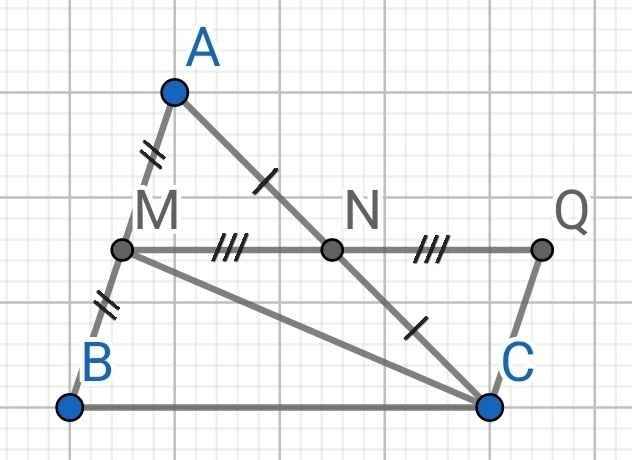
a) Xét ∆AMN và ∆CQN có:

AN = NC (do N là trung điểm của AC)

∠ANM = ∠CNQ (đối đỉnh)

NM = NQ (gt)

⇒ ∆AMN = ∆CQN (c-g-c)

b) Do ∆AMN = ∆CQN (cmt)

⇒ ∠MAN = ∠NCQ (hai góc tương ứng)

Mà ∠MAN và ∠NCQ là hai góc so le trong

⇒ AM // CQ

⇒ MB // CQ

c) Do ∆AMN = ∆CQN (cmt)

⇒ AM = CQ (hai cạnh tương ứng)

Mà AM = MB (do M là trung điểm của AB)

⇒ MB = CQ

Do BM // CQ (cmt)

⇒ ∠BMC = ∠QCM (so le trong)

Xét ∆BMC và ∆QCM có:

BM = CQ (cmt)

∠BMC = ∠QCM (cmt)

CM là cạnh chung

⇒ ∆BMC = ∆QCM (c-g-c)

⇒ BC = MQ (hai cạnh tương ứng)

Do NM = NQ (gt)

⇒ MN = 1/2 MQ

Mà BC = MQ (cmt)

⇒ MN = 1/2 BC

tự nghĩ đi