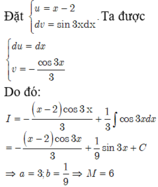Hãy tính: 2sin 30 ° - 2cos 60 ° + tg 45 °

Những câu hỏi liên quan
Tính
a. 2sin 30 - 2cos 60 + tan 45
b. sin 45 + cot 60.cos 30
c. cot 44.cot 45.cot 46
Tính giá trị của biểu thức
a) A = 2sin 30 độ + 3 cos 45 độ - sin 60 độ
b) B = 3 cos 30 độ + 3 sin 45 độ - cos 60 độ
a) \(A=2sin30^o+3cos45^o-sin60^0\)
\(\Leftrightarrow A=2.\dfrac{1}{2}+3.\dfrac{\sqrt[]{2}}{2}-\dfrac{\sqrt[]{3}}{2}\)
\(\Leftrightarrow A=1+\dfrac{3\sqrt[]{2}}{2}-\dfrac{\sqrt[]{3}}{2}\)
\(\Leftrightarrow A=1+\dfrac{\sqrt[]{3}\left(\sqrt[]{6}-1\right)}{2}\)
b) \(B=3cos30^o+3sin45^o-cos45^o\)
\(\Leftrightarrow B=3\dfrac{\sqrt[]{3}}{2}+3\dfrac{\sqrt[]{2}}{2}-\dfrac{\sqrt[]{2}}{2}\)
\(\Leftrightarrow B=\dfrac{3\sqrt[]{3}}{2}+\dfrac{2\sqrt[]{2}}{2}\)
\(\Leftrightarrow B=\dfrac{3\sqrt[]{3}}{2}+\sqrt[]{2}\)
Đúng 1
Bình luận (0)
Tính giá trị biểu thức
1) 2sin 30° - 2cos 60° + tan45°
2) sin45° + cot 60° ×cos30°
1) \(2.\sin30^o-2.\cos60^o+\tan45^o\)
\(=2.\frac{1}{2}-2.\frac{1}{2}+1=1\)
2) \(\sin45^o+\cot60^o.\cot30^o\)
\(=\frac{\sqrt{2}}{2}+\frac{\sqrt{3}}{3}.\frac{\sqrt{3}}{2}=\frac{\sqrt{2}}{2}+\frac{3}{6}=\frac{\sqrt{2}}{2}+\frac{1}{2}=\frac{1+\sqrt{2}}{2}\)
Đúng 0
Bình luận (0)
B= tan^2 67°+ 2cos^2 16°-cotg^2 23° + 2sin^2 16°- 2cotg 37°/tan 53° A= cotg 67° . Cotg 23°-2(cos 45°. sin 64°)^2-2sin 23°/3cos 67°- sin^2 26°
\(B=tan^267^0-cot^223^0+2\cdot\left(sin^216^0+cos^216^0\right)-2\)
\(=0+2\cdot1-2=0\)
\(A=cot67\cdot tan67-2\left(\dfrac{\sqrt{2}}{2}\cdot sin64\right)^2-2\cdot\dfrac{sin23}{3\cdot sin23}-sin^226^0\)
\(=1-2\cdot\dfrac{1}{2}\cdot sin^264^0-\dfrac{2}{3}-sin^226^0\)
\(=1-1-\dfrac{2}{3}=-\dfrac{2}{3}\)
Đúng 1
Bình luận (0)
1) tính:
a) 2 sin 30 độ - 2 cos 60 độ + tg 45 độ
b) cotan 48 độ + cotan 45 độ+ cotan 45 độ
\(2\sin30^0-2cos60^0+\tan45^0\)
\(=2cos30^0-2cos30^0+1=1\)(Do trong tam giác có 2 góc phụ nhau thì sin góc này bằng cos góc kia)
Đúng 0
Bình luận (0)
\(\dfrac{1}{1-tg^22x}=1+cos4x\)
\(cotgx=\dfrac{sin^2x-2sin^2\left(\dfrac{\pi}{4}-x\right)}{cos^2x+2cos^2\left(\dfrac{\pi}{4}+x\right)}\)
Tính nguyên hàm :
a) I= \(\int\dfrac{dx}{2sin^2x+5sinx.cosx+2cos^2x}\)
b) I= \(\int\dfrac{dx}{sin^2x+3sinx.cox+2cos^2x}\)
\(a=\int\dfrac{1}{2tan^2x+5tanx+2}.\dfrac{dx}{cos^2x}\)
Đặt \(tanx=t\Rightarrow dt=\dfrac{dx}{cos^2x}\)
\(I=\int\dfrac{dt}{2t^2+5t+2}=\int\dfrac{dt}{\left(t+2\right)\left(2t+1\right)}=\dfrac{2}{3}\int\left(\dfrac{1}{2t+1}-\dfrac{1}{2t+4}\right)dt\)
\(=\dfrac{1}{3}ln\left|\dfrac{2t+1}{2t+4}\right|+C=\dfrac{1}{3}ln\left|\dfrac{2tanx+1}{2tanx+4}\right|+C\)
Câu b hoàn toàn tương tự
Đúng 1
Bình luận (1)
Tính nguyên hàm
I
∫
x
-
2
sin
3
x
d
x
-
x
-
2
cos
3
x
a
+
b
sin
3
x
Tính . Chọn đáp ánđúng: A. 6 B. 14 C. 34 D. 22
Đọc tiếp
Tính nguyên hàm I = ∫ x - 2 sin 3 x d x = - x - 2 cos 3 x a + b sin 3 x Tính . Chọn đáp án
đúng:
A. 6
B. 14
C. 34
D. 22
tính ạ
\(\dfrac{sin57^o}{cos33^o}+2sin^248^o\left(2024-2cos^248^o\right)\)
Chắc người ra đề có sự nhầm lẫn, hoặc là em ghi nhầm đề.
Biểu thức này ko thể rút gọn bằng tay. Chỉ có nhập máy rồi bấm. Nếu đằng trước ngoặc là dấu trừ thay vì dấu nhân thì rút gọn được.
Đúng 0
Bình luận (0)