Cho hàm số y = x + 2 x - 1 . Giá trị m i n x ∈ 2 ; 3 y 2 + m a x x ∈ 2 ; 3 y 2 bằng:
A. 16
B. 45 4
C. 25 4
D. 89 4
Bài 1. Cho hàm số
y= 2x-1
a) Tính giá trị của hàm số y khi x=0; x=1; x= -2
b) Tìm giá trị của x khi y=3
Bài 2. Cho hàm số
y= -3x
a) Vẽ đồ thị hàm số
b) Tìm trên đồ thị hàm số điểm có hoành độ bằng 2
c) Tìm trên đồ thị hàm số điểm có tung độ bằng -6
Bài 1:
a: x=0 => y=-1
x=1 =>y=1
Cho các hàm số \(y=-x+1\) và \(y=x\). Tính giá trị y theo giá trị x để hoàn thành bảng sau:
| \(x\) | -2 | -1 | 0 | 1 | 2 |
| \(y=-x+1\) | ? | ? | ? | ? | ? |
| \(y=x\) | ? | ? | ? | ? | ? |
Khi giá trị \(x\) tăng, giá trị \(y\) tương ứng của mỗi hàm số \(y=-x+1\) và \(y=x\) tăng hay giảm?
Thay x vào ta có:

Dựa vào bảng trên ta thấy:
Khi x tăng, giá trị y của hàm số y=-x+1 giảm
Khi x tăng, giá trị y của hàm số y=x tăng
Cho hàm số bậc nhất y=(m-1/2)x+2
a, với giá trị nào của m để hàm số là hàm số bậc nhất? Xác định các hệ số a,b
b, cho hàm số bậc nhất y=(m-1/2)x+2. Với giá trị nào của m thì hàm số đồng biến,nghịch biến.
c, cho hàm số bậc nhất y=0.5x+2. Tính giá trị của y khi biết giá trị của x=2
Bài 1 : Cho hàm số y=(m-3)x+4 . Với giá trị nào của m thì hàm số đồng biến, nghịch biến Bài 4: Cho hàm số y=(3-√2) x+1 a, Hàm số đồng biến hay nghịch biến? Vì sao? b, Tính các giá trị tương ứng của y khi x nhân các giá trị sau ; O, 1, √2, 3+√2, 3-√2
Bài 1:
Hàm số y=(m-3)x+4 đồng biến trên R khi m-3>0
=>m>3
Hàm số y=(m-3)x+4 nghịch biến trên R khi m-3<0
=>m<3
Bài 4:
a: Vì \(a=3-\sqrt{2}>0\)
nên hàm số \(y=\left(3-\sqrt{2}\right)x+1\) đồng biến trên R
b: Khi x=0 thì \(y=0\left(3-\sqrt{2}\right)+1=1\)
Khi x=1 thì \(y=\left(3-\sqrt{2}\right)\cdot1+1=3-\sqrt{2}+1=4-\sqrt{2}\)
Khi \(x=\sqrt{2}\) thì \(y=\left(3-\sqrt{2}\right)\cdot\sqrt{2}+1=3\sqrt{2}-2+1=3\sqrt{2}-1\)
Khi \(x=3+\sqrt{2}\) thì \(y=\left(3-\sqrt{2}\right)\left(3+\sqrt{2}\right)-1\)
=9-4-1
=9-5
=4
Khi \(x=3-\sqrt{2}\) thì \(y=\left(3-\sqrt{2}\right)^2-1\)
\(=11-6\sqrt{2}-1=10-6\sqrt{2}\)
Bài 1: Cho hàm số\(y=x\sqrt{m-1}-\dfrac{3}{2}\).Tìm giá trị của m sao cho hàm số trên là hàm số bậc nhất
Bài 2: Với giá trị nào của k thì:
a)Hàm số \(y=\left(k^2-5k-6\right)x-13\) đồng biến?
b)Hàm số \(y=\left(2k^2+3k-2\right)x+3\) nghịch biến?
Bài 3: Cho hai hàm số bậc nhất y = 2x + k và y = (2m + 1)x + 2k - 3. Tìm điều kiện đối với m và k để hai đồ thị hàm số là:
a)Hai đường thẳng cắt nhau
b)Hai đường thẳng song song với nhau
c)Hai đường thẳng trùng nhau
Bài 4: Cho đường thẳng (d): y = (m - 3)x + 1 - m. Xác định m trong các trường hợp sau đây:
a) (d) cắt trục Ox tại điểm A có hoành độ x = 2
b) (d) cắt trục tung Ox tại điểm B có tung độ y = -3
c) (d) đi qua điểm C(-1 ; 4)
Xét hàm số \(y = f\left( x \right) = \frac{{2{x^2} - 2}}{{x - 1}}\).
a) Bảng sau đây cho biết giá trị của hàm số tại một số điểm gần điểm 1.
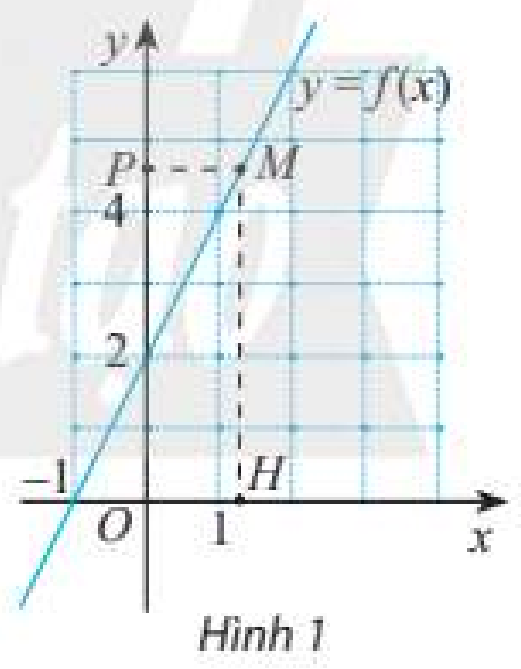
a) Khi \(x\) càng gần đến 1 thì giá trị của hàm số càng gần đến 4.
b) Khi điểm \(H\) thay đổi gần về điểm \(\left( {1;0} \right)\) trên trục hoành thì điểm \(P\) càng gần đến điểm \(\left( {0;4} \right)\).
Câu 1: Cho hàm số y = (3m + 5) x\(^2\) với m \(\ne\) \(\dfrac{-5}{3}\). Tìm các giá trị của tham số m để hàm số:
a) Nghịch biến với mọi x > 0
b) Đồng biến với mọi x >0
c) Đạt giá trị lớn nhất là 0
d) Đạt giá trị nhỏ nhất là 0
Câu 2: Cho hàm số y = \(\left(\sqrt{3k+4}-3\right)x^2\) với k \(\ge\dfrac{-4}{3}\); k \(\ne\dfrac{5}{3}\)
Tính các giá trị của tham số K để hàm số:
a) Nghịch biến với mọi x >0
b) Đồng biến với mọi x >0
Câu 1:
a) Để hàm số \(y=\left(3m+5\right)\cdot x^2\) nghịch biến với mọi x>0 thì \(3m+5< 0\)
\(\Leftrightarrow3m< -5\)
hay \(m< -\dfrac{5}{3}\)
Vậy: Để hàm số \(y=\left(3m+5\right)\cdot x^2\) nghịch biến với mọi x>0 thì \(m< -\dfrac{5}{3}\)
b) Để hàm số \(y=\left(3m+5\right)\cdot x^2\) đồng biến với mọi x>0 thì
3m+5>0
\(\Leftrightarrow3m>-5\)
hay \(m>-\dfrac{5}{3}\)
Vậy: Để hàm số \(y=\left(3m+5\right)\cdot x^2\) đồng biến với mọi x>0 thì \(m>-\dfrac{5}{3}\)
2.
Để hàm nghịch biến với x>0 \(\Leftrightarrow\sqrt{3k+4}-3< 0\)
\(\Leftrightarrow\sqrt{3k+4}< 3\Leftrightarrow3k+4< 9\)
\(\Rightarrow-\dfrac{4}{3}\le k< \dfrac{5}{3}\)
Để hàm đồng biến khi x>0
\(\Leftrightarrow\sqrt{3k+4}-3>0\Leftrightarrow\sqrt{3k+4}>3\)
\(\Leftrightarrow3k+4>9\Rightarrow k>\dfrac{5}{3}\)
1. Cho hàm số y=3x-1. Lập bảng giá trị tương ứng của y khi x= -1, -1/2, 1/2, 1, 3/2
2. a) Vẽ đồ thị hàm số y=1/2x
b) Tính giá trị của x khi y=-1, y=2, y=-0,5
Cho hàm số f(x) có đạo hàm là f'(x). Đồ thị của hàm số y = f'(x) được cho như hình vẽ dưới đây:
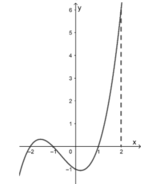
Biết rằng f(-1) + f(0) < f(1) + f(2). Giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = f(x) trên đoạn [-1;2] lần lượt là:
A. f(1);f(2)
B. f(2);f(0)
C. f(0);f(2)
D. f(1);f(-1)
Chọn A
Từ đồ thị của hàm số y = f'(x) ta có bảng biến thiên của hàm số y = f(x) trên đoạn [-1;2] như sau
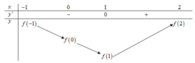
Nhận thấy
![]()
Để tìm ![]() ta so sánh f(-1) và f(2)
ta so sánh f(-1) và f(2)
Theo giả thiết, ![]()
![]()
Từ bảng biến thiên , ta có f(0) - f(1) > 0. Do đó f(2) - f(-1) > 0 ![]()
![]()
Cho hàm số y = f (x) =x(x -1) và y = g(t) = (x - 2016)^2. Hỏi có giá trị nào của x và t để giá trị hai hàm số bằng nhau không