
Câu 5 ạ, giải được câu 6 càng tốt ạ :)))))
Giải giúp mình ạ, làm được bao nhiêu câu cũng được ạ hết thì càng tốt ạ
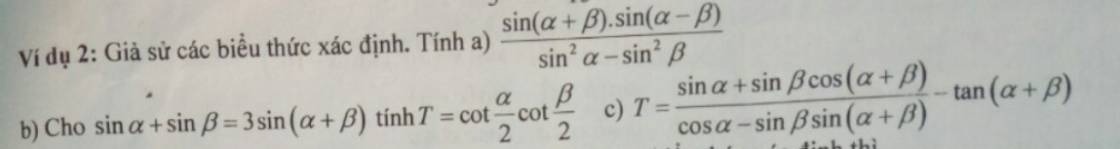
a: \(=\dfrac{-\dfrac{1}{2}\left[cos\left(a+b+a-b\right)-cos\left(a+b-a+b\right)\right]}{cos^2b-cos^2a}\)
\(=\dfrac{-\dfrac{1}{2}\cdot\left[cos2a-cos2b\right]}{\dfrac{1-cos2b}{2}-\dfrac{1-cos2a}{2}}\)
\(=\dfrac{-\dfrac{1}{2}\cdot\left(cos2a-cos2b\right)}{\dfrac{1-cos2b-1+cos2a}{2}}=\dfrac{-\dfrac{1}{2}\cdot\left(cos2a-cos2b\right)}{\dfrac{1}{2}\cdot\left(cos2a-cos2b\right)}=-1\)
c: \(T=\dfrac{sina+sinb\cdot\left(cosa\cdot cosb-sina\cdot sinb\right)}{cosa-sinb\cdot\left(sina\cdot cosb+sinb\cdot cosa\right)}-tan\left(a+b\right)\)
\(=\dfrac{sina+sinb\cdot cosa\cdot cosb-sin^2b\cdot sina}{cosa-sinb\cdot sina\cdot cosb-sin^2b\cdot cosa}-tan\left(a+b\right)\)
\(=\dfrac{sina\left(1-sin^2b\right)+sinb\cdot cosa\cdot cosb}{cosa\left(1-sin^2b\right)-sinb\cdot sina\cdot cosb}\)-tan(a+b)
\(=\dfrac{sina\cdot cos^2b+sinb\cdot cosa\cdot cosb}{cosa\cdot cos^2b-sinb\cdot sina\cdot cosb}-tan\left(a+b\right)\)
\(=\dfrac{sina\cdot cosb+sinb\cdot cosa}{cosa\cdot cosb-sina\cdot sinb}-tan\left(a+b\right)\)
\(=\dfrac{sin\left(a+b\right)}{cos\left(a+b\right)}-tan\left(a+b\right)=0\)
giải giúp mình câu 5 với ạ thêm mấy câu kia càng tốt
Bài 4
a, Số nu của gen là 90 x 20 = 1800 ( nu )
=> Chiều dài của gen \(\dfrac{1800}{2}.3,4=3060\left(A^O\right)\)
b,
Số nu của cả gen A=T=1800.20% = 360 (nu)
G=X=1800.30% = 540(nu)
Số nu từng mạch :
A1 = T2 = 15% . 900 = 135 ( nu )
T1 = A2 = 360 - 135 = 225 ( nu )
G1 = X2 = 540 - X1 = 540 - 360 = 180 ( nu )
X1 = G2 = 40% . 900 = 360 ( nu )
Bài 5
Ta có : \(\left\{{}\begin{matrix}H=2A+3G=N+G=3900\\G=900\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}A=T=600\left(nu\right)\\G=X=900\left(nu\right)\\N=3000,N1=N2=1500\left(nu\right)\end{matrix}\right.\)
A1 = T2 = 30%.1500= 450 (nu)
T1 = A2 = 600 - 450 = 150 (nu)
G1 = X2 = 10%.1500 = 150 ( nu )
G2 = X1 = 900 - 150 = 750 (nu)
giải dùm mình câu nào cũng dc ạ 😞 3 câu luôn càng tốt ạ
giải thích giúp mình vì sao chọn câu đó nhé (dịch được càng tốt ạ)

Chọn B nhé
Dịch câu gốc: Cha mẹ một vài lần nóng giận với các con của họ, nhưng suy cho cùng họ cũng chỉ muốn tốt cho con họ mà thôi
Dịch câu B: Nói chung, cha mẹ luôn yêu thương con cái mặc dù hay nóng giận với chúng trong một vài hoàn cảnh
Mình dịch ko sát nghĩa lắm nhưng nói chung là như thế
 giúp tớ vs tớ đg cần gấp ạ lm đc câu nào hay câu đấy ạ ( lm hết đc càng tốt có lời giải nha ) camon trccc ạ
giúp tớ vs tớ đg cần gấp ạ lm đc câu nào hay câu đấy ạ ( lm hết đc càng tốt có lời giải nha ) camon trccc ạ
Bài 1: - \(\dfrac{5}{7}\) x \(\dfrac{31}{33}\) + \(\dfrac{-5}{7}\) x \(\dfrac{2}{33}\) + 2\(\dfrac{5}{7}\)
= - \(\dfrac{5}{7}\) \(\times\) ( \(\dfrac{31}{33}\) + \(\dfrac{2}{33}\)) + 2 + \(\dfrac{5}{7}\)
= - \(\dfrac{5}{7}\) + 2 + \(\dfrac{5}{7}\)
= 2
2, \(\dfrac{3}{14}\): \(\dfrac{1}{28}\) - \(\dfrac{13}{21}\): \(\dfrac{1}{28}\) + \(\dfrac{29}{42}\): \(\dfrac{1}{28}\) - 8
= (\(\dfrac{3}{14}\) - \(\dfrac{13}{21}\) + \(\dfrac{29}{42}\)) : \(\dfrac{1}{28}\) - 8
= \(\dfrac{2}{7}\) x 28 - 8
= 8 - 8
= 0
3, \(\dfrac{37}{43}\) . \(\dfrac{17}{29}\) - \(\dfrac{21}{41}\).\(\dfrac{1}{2}\) + \(\dfrac{9}{58}\): 1\(\dfrac{6}{37}\) - \(\dfrac{6}{29}\): 1\(\dfrac{20}{21}\)
= \(\dfrac{37}{43}\). \(\dfrac{17}{29}\) - \(\dfrac{21}{41}\) . \(\dfrac{1}{2}\) + \(\dfrac{9}{58}\).\(\dfrac{37}{43}\) - \(\dfrac{6}{29}\).\(\dfrac{21}{41}\)
= (\(\dfrac{37}{43}\).\(\dfrac{17}{29}\) + \(\dfrac{9}{58}\).\(\dfrac{37}{43}\)) - (\(\dfrac{21}{41}\).\(\dfrac{1}{2}\) + \(\dfrac{6}{29}\).\(\dfrac{21}{41}\))
= \(\dfrac{37}{43}\).( \(\dfrac{17}{29}\) + \(\dfrac{9}{58}\)) - \(\dfrac{21}{41}\).( \(\dfrac{1}{2}\) + \(\dfrac{6}{29}\))
= \(\dfrac{37}{43}\).\(\dfrac{43}{58}\) - \(\dfrac{21}{41}\).\(\dfrac{41}{58}\)
= \(\dfrac{37}{58}\) - \(\dfrac{21}{58}\)
= \(\dfrac{16}{58}\)
= \(\dfrac{8}{29}\)
mọi người ơi giúp mình câu này với ạ, lời giải chi tiết càng tốt ạ, mình khá rối với câu này -.- cảm ơn mọi người nhiều
\(y'=\dfrac{\left(-2x+2\right)\left(x-3\right)-\left(-x^2+2x+c\right)}{\left(x-3\right)^2}=\dfrac{-x^2+6x-6-c}{\left(x-3\right)^2}\)
\(\Rightarrow\) Cực đại và cực tiểu của hàm là nghiệm của: \(-x^2+6x-6-c=0\) (1)
\(\Delta'=9-\left(6+c\right)>0\Rightarrow c< 3\)
Gọi \(x_1;x_2\) là 2 nghiệm của (1) \(\Rightarrow\left\{{}\begin{matrix}-x_1^2+6x_1-6=c\\-x_2^2+6x_2-6=c\end{matrix}\right.\)
\(\Rightarrow m-M=\dfrac{-x_1^2+2x_1+c}{x_1-3}-\dfrac{-x_2^2+2x_2+c}{x_2-3}=4\)
\(\Leftrightarrow\dfrac{-2x_1^2+8x_1-6}{x_1-3}-\dfrac{-2x_2^2+8x_2-6}{x_2-3}=4\)
\(\Leftrightarrow2\left(1-x_1\right)-2\left(1-x_2\right)=4\)
\(\Leftrightarrow x_2-x_1=2\)
Kết hợp với Viet: \(\left\{{}\begin{matrix}x_2-x_1=2\\x_1+x_2=6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=2\\x_2=4\end{matrix}\right.\)
\(\Rightarrow c=2\)
Có 1 giá trị nguyên

giúp mik câu 7 đến câu 15 lm được hết thì càng tốt ạ.
\(7,x^4+x^3+x^2-1=x^3\left(x+1\right)+\left(x-1\right)\left(x+1\right)=\left(x^3+x-1\right)\left(x+1\right)\)
\(8,x^2y^2+1-x^2-y^2=\left(x^2y^2-y^2\right)-\left(x^2-1\right)\\ =y^2\left(x^2-1\right)-\left(x^2-1\right)=\left(x-1\right)\left(x+1\right)\left(y-1\right)\left(y+1\right)\)
\(10,x^4-x^2+2x-1=x^4-\left(x-1\right)^2=\left(x^2-x+1\right)\left(x^2+x-1\right)\\ 11,3a-3b+a^2-2ab+b^2=3\left(a-b\right)+\left(a-b\right)^2=\left(3+a-b\right)\left(a-b\right)\\ 12,a^2+2ab+b^2-2a-2b+1=\left(a+b\right)^2-2\left(a+b\right)+1=\left(a+b-1\right)^2\\ 13,a^2-b^2-4a+4b=\left(a-b\right)\left(a+b\right)-4\left(a-b\right)=\left(a+b-4\right)\left(a-b\right)\\ 14,a^3-b^3-3a+3b=\left(a-b\right)\left(a^2+ab+b^2\right)-3\left(a-b\right)=\left(a-b\right)\left(a^2+ab+b^2-3\right)\\ 15,x^3+3x^2-3x-1=\left(x-1\right)\left(x^2+x+1\right)+3x\left(x-1\right)=\left(x-1\right)\left(x^2+4x+1\right)\)
1)
=0,25y.(64x3+z3)
2)
=x2(x2-4x+4)
=x2(x-2)2
5)
=x2(x+1)-4(x+1)
=(x2-4)(x+1)
=(x-2)(x+2)(x+1)
6)
=x2(x-1)-(x-1)
=(x2-1)(x-1)
=(x-1)(x+1)(x-1)
=(x-1)2(x+1)
Giải tự luận giúp em 1209 hoặc cả 2 câu thì càng tốt ạ
1209.
d nhận \(\overrightarrow{u}=\left(1;1;-1\right)\) là 1 vtcp
(P) nhận \(\overrightarrow{n}=\left(1;2;1\right)\) là 1 vtpt
Ta có: \(\overrightarrow{u_1}=\left[\overrightarrow{u};\overrightarrow{n}\right]=\left(3;-2;1\right)\)
\(\overrightarrow{u_2}=\left[\overrightarrow{u_1};\overrightarrow{n}\right]=\left(-4;-2;8\right)=-2\left(2;1;-4\right)\)
Phương trình d dạng tham số: \(\left\{{}\begin{matrix}x=t\\y=1+t\\z=2-t\end{matrix}\right.\)
Gọi M là giao điểm d và (P), tọa độ M thỏa mãn:
\(t+2\left(1+t\right)+2-t-4=0\Rightarrow t=0\Rightarrow M\left(0;1;2\right)\)
Do đó hình chiếu của d lên (P) nhận (2;1;-4) là 1 vtcp và đi qua M(0;1;2)
Phương trình: \(\dfrac{x}{2}=\dfrac{y-1}{1}=\dfrac{z-2}{-4}\)
Câu 1210 hoàn toàn tương tự
Cách làm nói chung:
- Tìm vecto chỉ phương \(\overrightarrow{u}\) của đường d và vtpt \(\overrightarrow{n}\) của mặt (P)
- Tính tích có hướng \(\overrightarrow{u_1}=\left(\overrightarrow{u};\overrightarrow{n}\right)\)
- Tiếp tục tính tích có hướng \(\overrightarrow{u_2}=\left[\overrightarrow{u_1};\overrightarrow{n}\right]\)
- Tìm tọa độ giao điểm M của d và (P)
- Hình chiếu vuông góc của d lên (P) sẽ đi qua M và nhận \(\overrightarrow{u_2}\) (hoặc 1 vecto cùng phương với nó) là 1 vtcp
Lưu ý rằng có vô số cách viết 1 pt đường thẳng (tùy thuộc cách chọn điểm) nên có thể trong 4 đáp án của đề bài không đáp án nào giống pt vừa viết được. Lúc đó cần kiểm tra bằng cách: 1. Loại những đáp án không giống vecto chỉ phương. 2. Trong những đáp án còn lại, tìm 1 điểm trên đó và thay vào pt đường thẳng vừa viết được, nếu thỏa mãn thì đó là đáp án đúng.
Giúp mình câu 47 và 48 với ạ. Có giải thích càng tốt🥺
47. B
result in: dẫn đến
48. B
financial aid: trợ cấp tài chính