giúp mình câu này với ạ
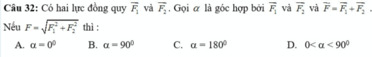
Giúp mình câu này với ạ, đc thì giải chi tiết giúp mình luôn ạ, đbt là câu b, mình hơi chậm hiểu 
Nãy ghi nhầm =="
a)Hđ gđ là nghiệm pt
`x^2=2x+2m+1`
`<=>x^2-2x-2m-1=0`
Thay `m=1` vào pt ta có:
`x^2-2x-2-1=0`
`<=>x^2-2x-3=0`
`a-b+c=0`
`=>x_1=-1,x_2=3`
`=>y_1=1,y_2=9`
`=>(-1,1),(3,9)`
Vậy tọa độ gđ (d) và (P) là `(-1,1)` và `(3,9)`
b)
Hđ gđ là nghiệm pt
`x^2=2x+2m+1`
`<=>x^2-2x-2m-1=0`
PT có 2 nghiệm pb
`<=>Delta'>0`
`<=>1+2m+1>0`
`<=>2m> -2`
`<=>m> 01`
Áp dụng hệ thức vi-ét:`x_1+x_2=2,x_1.x_2=-2m-1`
Theo `(P):y=x^2=>y_1=x_1^2,y_2=x_2^2`
`=>x_1^2+x_2^2=14`
`<=>(x_1+x_2)^2-2x_1.x_2=14`
`<=>4-2(-2m-1)=14`
`<=>4+2(2m+1)=14`
`<=>2(2m+1)=10`
`<=>2m+1=5`
`<=>2m=4`
`<=>m=2(tm)`
Vậy `m=2` thì ....
mọi người ơi giúp mình câu này với ạ, lời giải chi tiết càng tốt ạ, mình khá rối với câu này -.- cảm ơn mọi người nhiều
\(y'=\dfrac{\left(-2x+2\right)\left(x-3\right)-\left(-x^2+2x+c\right)}{\left(x-3\right)^2}=\dfrac{-x^2+6x-6-c}{\left(x-3\right)^2}\)
\(\Rightarrow\) Cực đại và cực tiểu của hàm là nghiệm của: \(-x^2+6x-6-c=0\) (1)
\(\Delta'=9-\left(6+c\right)>0\Rightarrow c< 3\)
Gọi \(x_1;x_2\) là 2 nghiệm của (1) \(\Rightarrow\left\{{}\begin{matrix}-x_1^2+6x_1-6=c\\-x_2^2+6x_2-6=c\end{matrix}\right.\)
\(\Rightarrow m-M=\dfrac{-x_1^2+2x_1+c}{x_1-3}-\dfrac{-x_2^2+2x_2+c}{x_2-3}=4\)
\(\Leftrightarrow\dfrac{-2x_1^2+8x_1-6}{x_1-3}-\dfrac{-2x_2^2+8x_2-6}{x_2-3}=4\)
\(\Leftrightarrow2\left(1-x_1\right)-2\left(1-x_2\right)=4\)
\(\Leftrightarrow x_2-x_1=2\)
Kết hợp với Viet: \(\left\{{}\begin{matrix}x_2-x_1=2\\x_1+x_2=6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=2\\x_2=4\end{matrix}\right.\)
\(\Rightarrow c=2\)
Có 1 giá trị nguyên
 Giúp mình câu này với ạ, mình đang cần gấp ạ
Giúp mình câu này với ạ, mình đang cần gấp ạ
a) Cl2 + 2NaOH --> NaClO + NaCl + H2O
Chất oxh: Cl2, chất khử: Cl2
| Sự oxh | Cl0 -1e--> Cl+1 | x1 |
| Sự khử | Cl0 +1e--> Cl-1 | x1 |
b) \(n_{Cl_2}=\dfrac{17,92}{22,4}=0,8\left(mol\right);n_{NaOH}=0,5.4=2\left(mol\right)\)
PTHH: Cl2 + 2NaOH --> NaClO + NaCl + H2O
_____0,8---->1,6--------->0,8---->0,8
=> \(\left\{{}\begin{matrix}C_{M\left(NaCl\right)}=\dfrac{0,8}{0,5}=1,6M\\C_{M\left(NaClO\right)}=\dfrac{0,8}{0,5}=1,6M\\C_{M\left(NaOH\right)}=\dfrac{2-1,6}{0,5}=0,8M\end{matrix}\right.\)

Giúp mình câu này với ạ, mình đang cần gấp ạ
 Giúp mình câu này với ạ, mình đang cần gấp ạ
Giúp mình câu này với ạ, mình đang cần gấp ạ
Bài 1.
a)Gia tốc vật: \(a=\dfrac{F}{m}=\dfrac{0,2}{0,1}=2\)m/s2
Vận tốc vật: \(v^2-v^2_0=2aS\)
\(\Rightarrow v=\sqrt{2aS}=\sqrt{2\cdot2\cdot10}=\sqrt{40}\approx6,3\)m/s
b)Với \(v'=10\)m/s thì gia tốc vật là:
\(a'=\dfrac{v'^2-v^2_0}{2S}=\dfrac{10^2-0}{2\cdot10}=5\)m/s2
Lực kéo lúc này: \(F'=m\cdot a'=0,1\cdot5=0,5N\)
Công của lực kéo F là:
\(A=F'\cdot s=0,5\cdot10=5J\)

Giúp mình câu này với ạ, mình đang cần gấp ạ
https://hoidap247.com/cau-hoi/558074
tham khảo ạ
nH2SO4=0,045mol nKOH=0,03
PT: X + H2SO4 ==> XSO4 + H2 (1)
H2SO4 + 2KOH ==> K2SO4 + 2H2O (2)
Từ 1 --> nH2SO4 dư = 0,015
--> nX=nH2SO4 pứ= 0,045-0,015=0,03
MX=1,2:0,03=40 --> X là Ca

Giúp mình câu này với ạ, mình đang cần gấp ạ
a)
Fe không phản ứng với H2SO4 đặc nguội
\(n_{SO_2}=\dfrac{1,176}{22,4}=0,0525\left(mol\right)\)
PTHH: Cu + 2H2SO4 --> CuSO4 + SO2 + 2H2O
0,0525<-0,105<----0,0525<-0,0525
\(\%m_{Cu}=\dfrac{0,0525.64}{27}.100\%=12,44\%\)
\(\%m_{Fe}=100\%-12,44\%=87,56\%\)
b) \(C_{M\left(dd.H_2SO_4\right)}=\dfrac{0,105}{0,8}=0,13125M\)
c) nNaOH = 1,25.0,5 = 0,625 (mol)
PTHH: 2NaOH + CuSO4 --> Cu(OH)2 + Na2SO4
Xét tỉ lệ: \(\dfrac{0,625}{2}>\dfrac{0,0525}{1}\) => NaOH dư, CuSO4 hết
PTHH: 2NaOH + CuSO4 --> Cu(OH)2 + Na2SO4
0,105<---0,0525------------------>0,0525
=> \(\left\{{}\begin{matrix}C_{M\left(NaOH_{dư}\right)}=\dfrac{0,625-0,105}{0,5}=1,04M\\C_{M\left(Na_2SO_4\right)}=\dfrac{0,0525}{0,5}=0,105M\end{matrix}\right.\)
a, nH2 = \(\dfrac{\dfrac{1176}{1000}}{22,4}=0,0525\left(mol\right)\)
PTHH: Cu + 2H2SO4(đặc, nguội) ---> CuSO4 + SO2 + 2H2O
0,0525 0,105 0,0525 0,0525
=> \(\left\{{}\begin{matrix}m_{Cu}=0,0525.64=3,36\left(g\right)\\m_{Fe}=27-3,36=23,64\left(g\right)\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}\%m_{Cu}=\dfrac{3,36}{27}=12,44\%\\\%m_{Fe}=100\%-12,44\%=87,56\%\end{matrix}\right.\)
b, \(C_{MddH_2SO_4}=\dfrac{0,105}{\dfrac{800}{1000}}0,13125M\)
c, nNaOH = 1,25.\(\dfrac{500}{1000}\) = 0,625 (mol)
PTHH: CuSO4 + 2NaOH ---> Cu(OH)2 + Na2SO4
LTL: 0,0525 < \(\dfrac{0,625}{2}\) => NaOH dư
Theo pthh: \(\left\{{}\begin{matrix}n_{NaOH\left(pư\right)}=2n_{CuSO_4}=2.0,0525=0,105\left(mol\right)\\n_{Cu\left(OH\right)_2}=n_{Na_2SO_4}=n_{CuSO_4}=0,0525\left(mol\right)\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}C_{MNaOH\left(dư\right)}=\dfrac{0,625-0,105}{0,5}=1,04M\\C_{MNa_2SO_4}=\dfrac{0,0525}{0,5}=0,105M\end{matrix}\right.\)
giúp mình với ạ, mình đang cần gấp 2 câu này ạ.

Gọi vận tốc ca nô là x ( x > 0 )
Theo bài ra ta có pt \(\dfrac{72}{x+3}+\dfrac{54}{x-3}=6\Rightarrow x=21\left(tm\right)\)
GIÚP MÌNH 4 CÂU ĐỌC HIỂU NÀY VỚI Ạ!!
KHÔNG CHÉP MẠNG NHÉ!!
GIÚP MÌNH VỚI Ạ!!! HU HU HU!!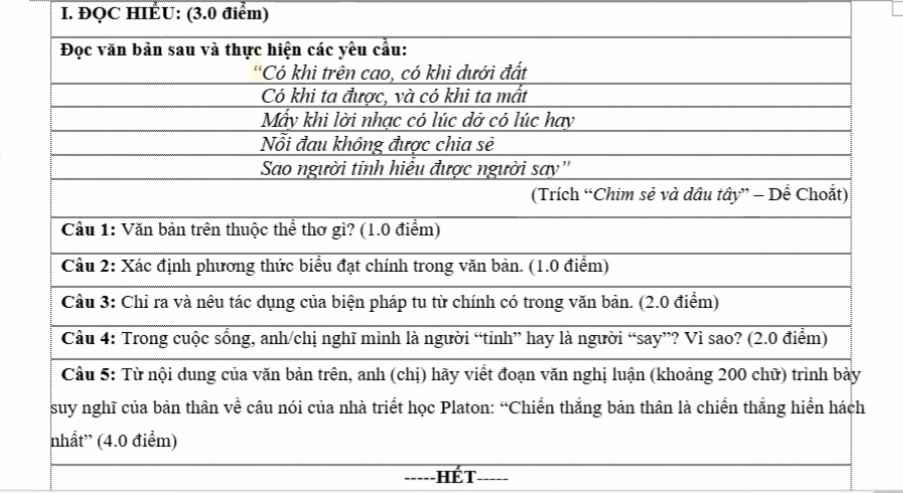
Giúp mình câu này với ạ, mình đang rất cần ạ😥😥