Có bao nhiêu số nguyên m để bất phương trình x 6 + 6 x 4 + 15 - 3 m 2 x 2 - 6 m x + 10 ≥ 0 nghiệm đúng với mọi số thực x.
A. 4
B. 3
C. Vô số
D. 5
Cho bất phương trình 3 + x + 6 - x - 18 + 3 x - x 2 ≤ m 2 - m + 1 (m là tham số). Có bao nhiêu giá trị nguyên của m thuộc[-5;5] để bất phương trình nghiệm đúng với mọi x ∈ - 3 ; 6 ?
A. 3
B. 5
C. 9
D. 10
Đặt ![]()
Suy ra ![]()
Ta có ![]()
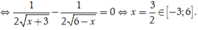
Ta có bảng biến thiên
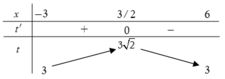
Từ bảng biến thiên ta suy ra ![]()
Khi đó bất phương trình trở thành: ![]()
![]()
Xét hàm số ![]() với
với ![]()
Ta có ![]()
Suy ra hàm số f(t) nghịch biến trên ![]()
![]()
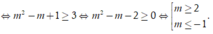
Chọn C.
Cho hàm số y = f(x) có bảng biến thiên:

Có tất cả bao nhiêu giá trị nguyên của m không vượt quá 10 để bất phương trình f log 2 10 − x − x − 6 ≤ m có nghiệm?
A. 15.
B. 16.
C. 17.
D. 14.
Có bao nhiêu giá trị nguyên của tham số mÎ[-10;10] để bất phương trình sau nghiệm đúng ∀ x ∈ R : 6 + 2 7 x + 2 - m 3 - 7 x - m + 1 2 x ≥ 0
A. 10
B. 9
C. 12
D. 11
Có bao nhiêu giá trị nguyên của tham số m để phương trình 6 + x - 2 - x - 3 + x - 6 - x - 5 - m = 0 có nghiệm thực
A. 0
B. 2
C. 3
D. 1
Có bao nhiêu số nguyên của tham số m để phương trình \(\sqrt{x+3}+\sqrt{6-x}-\sqrt{\left(x+3\right)\left(6-x\right)}=m\)
có nghiệm
ĐK: \(-3\le x\le6\)
Đặt \(\sqrt{x+3}+\sqrt{6-x}=t\left(3\le t\le3\sqrt{2}\right)\)
\(\Rightarrow\sqrt{\left(x+3\right)\left(6-x\right)}=\dfrac{t^2-9}{2}\)
\(\sqrt{x+3}+\sqrt{6-x}-\sqrt{\left(x+3\right)\left(6-x\right)}=m\)
\(\Leftrightarrow m=f\left(t\right)=\dfrac{-t^2+2t+9}{2}\)
Yêu cầu bài toán thỏa mãn khi \(minf\left(t\right)\le m\le maxf\left(x\right)\)
\(\Leftrightarrow\dfrac{-9+6\sqrt{2}}{2}\le m\le3\)
có bao nhiêu số nguyên của tham số m để phương trình \(\sqrt{x+3}+\sqrt{6-x}-\sqrt{\left(x+3\right)\left(6-x\right)}=m\) có nghiệm
ĐKXĐ: \(-3\le x\le6\)
Đặt \(\sqrt{x+3}+\sqrt{6-x}=t\)
Ta có: \(t=\sqrt{x+3}+\sqrt{6-x}\ge\sqrt{x+3+6-x}=3\)
\(t\le\sqrt{2\left(x+3+6-x\right)}=3\sqrt{2}\)
\(\Rightarrow3\le t\le3\sqrt{2}\)
Lại có:
\(t^2=9+2\sqrt{\left(x+3\right)\left(6-x\right)}\Rightarrow-\sqrt{\left(x+3\right)\left(6-x\right)}=\dfrac{9-t^2}{2}\)
Phương trình trở thành:
\(t+\dfrac{9-t^2}{2}=m\Leftrightarrow m=-\dfrac{1}{2}t^2+t+\dfrac{9}{2}\)
Xét hàm \(f\left(t\right)=-\dfrac{1}{2}t^2+t+\dfrac{9}{2}\) trên \(\left[3;3\sqrt{2}\right]\)
\(-\dfrac{b}{2a}=1\notin\left[3;3\sqrt{2}\right]\)
\(f\left(3\right)=3\) ; \(f\left(3\sqrt{2}\right)=\dfrac{-9+6\sqrt{2}}{2}\)
\(\Rightarrow\dfrac{-9+6\sqrt{2}}{2}\le f\left(t\right)\le3\)
\(\Rightarrow\) Phương trình có nghiệm khi \(\dfrac{-9+6\sqrt{2}}{2}\le m\le3\)
Có 4 giá trị nguyên của m thỏa mãn
Có bao nhiêu số nguyên của m để phương trình \({x^4} - 10{x^3} - 2(m - 11){x^2} + 2(5m + 6)x + {m^2} + 2m = 0\) có bốn nghiệm phân biệt thuộc \(( - 2; + \infty )\) ?
Giải bất phương trình: 2 2 x - 5 . 2 x + 6 ≤ 0 .Có bao nhiêu giá trị nguyên của x thỏa mãn bất phương trình trên
A. 2
B. 3
C. 4
D. 1
Cho bất phương trình m 2 - x + 12 4 - x 2 ≥ 16 x + 3 m 2 + x + 3 m + 35 Có tất cả bao nhiêu giá trị nguyên của tham số m ∈ - 10 ; 10 để bất phương trình nghiệm đúng với mọi x ∈ - 2 ; 2 ?
A. 10
B. 18.
C. 3.
D. 4.
Cho bất phương trình m 2 - x + 12 4 - x 2 ≥ 16 x + 3 m 2 + x + 3 m + 35 .Có tất cả bao nhiêu giá trị nguyên của tham số m ∈ - 10 ; 10 để bất phương trình nghiệm đúng với mọi x ∈ - 2 ; 2 ?
A. 10.
B. 18.
C. 3.
D. 4.
Chọn C
![]()
![]()
![]()
![]()
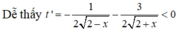
nên hàm t = t (x) nghịch biến trên (-2;2)
![]()
![]()
Thay vào bất phương trình trên được:
![]()
![]()
Bất phương trình đã cho nghiệm đúng với mọi x ∈ - 2 ; 2 nếu và chỉ nếu bất phương trình
![]()
nghiệm đúng với mọi t ∈ - 6 ; 2
tam thức bậc hai f t = 2 t 2 - m t + 3 m - 5 có hai nghiệm thỏa mãn
![]()
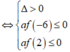
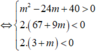
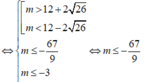
Kết hợp với m ∈ - 10 ; 10 thì m ∈ - 10 ; - 9 ; - 8