Đặt ![]()
Suy ra ![]()
Ta có ![]()
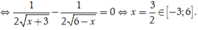
Ta có bảng biến thiên
Từ bảng biến thiên ta suy ra ![]()
Khi đó bất phương trình trở thành: ![]()
![]()
Xét hàm số ![]() với
với ![]()
Ta có ![]()
Suy ra hàm số f(t) nghịch biến trên ![]()
![]()
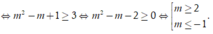
Chọn C.
Đặt ![]()
Suy ra ![]()
Ta có ![]()
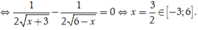
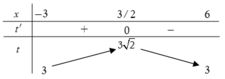
Ta có bảng biến thiên

Từ bảng biến thiên ta suy ra ![]()
Khi đó bất phương trình trở thành: ![]()
![]()
Xét hàm số ![]() với
với ![]()
Ta có ![]()
Suy ra hàm số f(t) nghịch biến trên ![]()
![]()
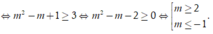
Chọn C.
Số giá trị nguyên của tham số m ∈ - 10 ; 10 để bất phương trình 3 + x + 6 - x - 18 + 3 x - x 2 ≤ m 2 - m + 1 nghiệm đúng ∀ x ∈ - 3 ; 6 là
A. 28
B. 20
C. 4
D. 19
Số giá trị nguyên của tham số mÎ[-10;10] để bất phương trình 3 + x + 6 - x - 18 + 3 x - x 2 ≤ m 2 - m + 1 nghiệm đúng ∀ x ∈ [ - 3 ; 6 ] là
A. 28
B. 20
C. 4
D. 19
Cho bất phương trình m 2 - x + 12 4 - x 2 ≥ 16 x + 3 m 2 + x + 3 m + 35 Có tất cả bao nhiêu giá trị nguyên của tham số m ∈ - 10 ; 10 để bất phương trình nghiệm đúng với mọi x ∈ - 2 ; 2 ?
A. 10
B. 18.
C. 3.
D. 4.
Cho bất phương trình m . 3 x + 1 + ( 3 m + 2 ) ( 4 - 7 ) x + ( 4 + 7 ) x > 0 với m là tham số. Tìm tất cả các giá trị của tham số m để bất phương trình đã cho có nghiệm đúng với mọi x ∈ - ∞ ; 0
A. m ≥ 2 - 2 3 3
B. m > 2 - 2 3 3
C. m > 2 + 2 3 3
D. m ≥ - 2 - 2 3 3
Có bao nhiêu giá trị nguyên của tham số m để phương trình 6 + x - 2 - x - 3 + x - 6 - x - 5 - m = 0 có nghiệm thực
A. 0
B. 2
C. 3
D. 1
Có tất cả bao nhiêu giá trị của tham số m để bất phương trình log 2 x 2 + m x + m + 2 ≥ log 2 x 2 + 2 nghiệm đúng với mọi x ∈ ℝ
A. 2
B. 4
C. 3
D. 1
Có bao nhiêu giá trị nguyên của tham số mÎ[-10;10] để bất phương trình sau nghiệm đúng ∀ x ∈ R : 6 + 2 7 x + 2 - m 3 - 7 x - m + 1 2 x ≥ 0
A. 10
B. 9
C. 12
D. 11
Tìm tất cả các giá trị thực của tham số m để bất phương trình 3 x + 3 + 5 - 3 x ≤ m có nghiệm đúng với mọi x ∈ ( - ∞ ; log 3 5 ]
A. m ≥ 2 2
B. m ≥ 4
C. m ≤ 4
D. m ≤ 2 2
Tìm tất cả các giá trị thực của tham số m để bất phương trình 2 x + 3 + 5 - 2 x ≤ m nghiệm đúng với mọi x ∈ - ∞ ; log 2 5
A. m ≥ 4
B. m < 4
C. m ≥ 2 2
D. m < 2 2