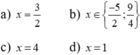\(a,2x\left(x-5\right)+4\left(x-5\right)=0\\ \Leftrightarrow\left(x-5\right)\left(2x+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-5=0\\2x+4=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=5\\2x=-4\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=5\\x=-2\end{matrix}\right.\)

Vậy \(x\in\left\{5;-2\right\}\)

\(b,3x-15=2x\left(x-5\right)\\ \Leftrightarrow3\left(x-5\right)-2x\left(x-5\right)=0\\ \Leftrightarrow\left(x-5\right)\left(-2x+3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-5=0\\-2x+3=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=5\\2x=3\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=5\\x=\dfrac{3}{2}\end{matrix}\right.\)

Vậy \(x\in\left\{5;\dfrac{3}{2}\right\}\)

\(c,\left(2x+1\right)\left(3x-2\right)=\left(5x-8\right)\left(2x+1\right)\\ \Leftrightarrow\left(2x+1\right)\left(3x-2\right)-\left(5x-8\right)\left(2x+1\right)=0\\ \Leftrightarrow\left(2x+1\right)\left(3x-2-5x+8\right)=0\\ \Leftrightarrow\left(2x+1\right)\left(-2x+6\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}2x+1=0\\-2x+6=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}2x=-1\\2x=6\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=3\end{matrix}\right.\)

Vậy \(x\in\left\{-\dfrac{1}{2};3\right\}\)

Câu d xem lại đề

\(a,\dfrac{x-3}{x}=\dfrac{x-3}{x+3}\)\(\left(đk:x\ne0,-3\right)\)

\(\Leftrightarrow\dfrac{x-3}{x}-\dfrac{x-3}{x+3}=0\)

\(\Leftrightarrow\dfrac{\left(x-3\right)\left(x+3\right)-x\left(x-3\right)}{x\left(x+3\right)}=0\)

\(\Leftrightarrow x^2-9-x^2+3x=0\)

\(\Leftrightarrow3x-9=0\)

\(\Leftrightarrow3x=9\)

\(\Leftrightarrow x=3\left(n\right)\)

Vậy \(S=\left\{3\right\}\)

\(b,\dfrac{4x-3}{4}>\dfrac{3x-5}{3}-\dfrac{2x-7}{12}\)

\(\Leftrightarrow\dfrac{4x-3}{4}-\dfrac{3x-5}{3}+\dfrac{2x-7}{12}>0\)

\(\Leftrightarrow\dfrac{3\left(4x-3\right)-4\left(3x-5\right)+2x-7}{12}>0\)

\(\Leftrightarrow12x-9-12x+20+2x-7>0\)

\(\Leftrightarrow2x+4>0\)

\(\Leftrightarrow2x>-4\)

\(\Leftrightarrow x>-2\)

`5-(x-6)=4(3-2x)`

`<=>5-x+6-4(3-2x)=0`

`<=> 5-x+6-12 +8x=0`

`<=> 7x -1=0`

`<=> 7x=1`

`<=>x=1/7`

Vậy pt đã cho có nghiệm `x=1/7`

__

`3-x(1-3x) =5(1-2x)`

`<=> 3-x+3x^2=5-10x`

`<=> 3-x+3x^2-5+10x=0`

`<=> 3x^2 +9x-2=0`

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-9+\sqrt{105}}{6}\\x=\dfrac{-9-\sqrt{105}}{6}\end{matrix}\right.\)

Vậy pt đã cho có tập nghiệm \(S=\left\{\dfrac{-9+\sqrt{105}}{6};\dfrac{-9-\sqrt{106}}{5}\right\}\)

__

`(x-3)(x+4) -2(3x-2)=(x-4)^2`

`<=>x^2+4x-3x-12- 6x +4 =x^2 -8x+16`

`<=>x^2-5x-8=x^2-8x+16`

`<=> x^2 -5x-8-x^2+8x-16=0`

`<=> 3x-24=0`

`<=>3x=24`

`<=>x=8`

Vậy pt đã cho có nghiệm `x=8`

a) 5-(x-6)=4(3-2x)

=> 5 – x + 6 = 12 – 8x

=> -x + 8x = 12 – 5 – 6

=> 7x = 1

=> x=1/7

Vậy phương trình có nghiệm x=1/7

 b) 3 - x ( 1 - 3x)=5(1-2x)

=> 3-x+3x^2=5-10x

=> 3x^2+9x-2= 0

0=105

=> x =\(\dfrac{-9-\sqrt{105}}{6}\)

\(a,\left(x-6\right)\left(2x-5\right)\left(3x+9\right)=0\Leftrightarrow\left[{}\begin{matrix}x-6=0\Leftrightarrow x=6\\2x-5=0\Leftrightarrow x=\dfrac{5}{2}\\3x+9=0\Leftrightarrow x=-3\end{matrix}\right.\)

\(b,2x\left(x-3\right)+5\left(x-3\right)=0\Leftrightarrow\left(2x+5\right)\left(x-3\right)=0\Leftrightarrow\left[{}\begin{matrix}x-3=0\Leftrightarrow x=3\\2x+5=0\Leftrightarrow x=-\dfrac{5}{2}\end{matrix}\right.\)

\(c,x^2-4-\left(x-2\right)\left(3-2x\right)=0\Leftrightarrow\left(x-2\right)\left(x+2\right)-\left(x-2\right)\left(3-2x\right)=0\Leftrightarrow\left(x-2\right)\left(x+2-3+2x\right)=0\Leftrightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{1}{3}\end{matrix}\right.\)

\(x=-7\left(2m-5\right)x-2m^2+8\Leftrightarrow x+7\left(2m-5\right)=8-2m^2\Leftrightarrow x\left(14m-34\right)=8-2m^2\)

\(ycđb\Leftrightarrow14m-34\ne0\Leftrightarrow m\ne\dfrac{34}{14}\)\(\Rightarrow x=\dfrac{8-2m^2}{14m-34}\)

\(3.17\Leftrightarrow4x^2-4x+1-2x-1=0\Leftrightarrow4x^2-6x=0\Leftrightarrow x\left(4x-6\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{3}{2}\end{matrix}\right.\)

3.15:

a, \(\Leftrightarrow\left\{{}\begin{matrix}x-6=0\\2x-5=0\\3x+9=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=6\\x=\dfrac{5}{2}\\x=-\dfrac{9}{3}=-3\end{matrix}\right.\)

b, \(\Leftrightarrow\left(x-3\right)\left(2x+5\right)=0\)

\(\Leftrightarrow\left\{{}\begin{matrix}x-3=0\\2x+5=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\x=-\dfrac{5}{2}\end{matrix}\right.\)

c, \(\Leftrightarrow\left(x-2\right)\left(x+2\right)-\left(x-2\right)\left(3-2x\right)=0\)

\(\Leftrightarrow\left(x-2\right)\left(x+2-3+2x\right)=0\)

\(\Leftrightarrow\left\{{}\begin{matrix}x-2=0\\3x-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\x=\dfrac{1}{3}\end{matrix}\right.\)

3.16

\(\Leftrightarrow\left(2m-5\right).-7-2m^2+8=0\)

\(\Leftrightarrow-14m+35-2m^2+8=0\)

\(\Leftrightarrow-14m-2m^2+43=0\)

\(\Leftrightarrow-2\left(7m+m^2\right)=-43\)

\(\Leftrightarrow m\left(7-m\right)=\dfrac{43}{2}\)

\(\Leftrightarrow\dfrac{m\left(7-m\right)}{1}-\dfrac{43}{2}=0\)

\(\Leftrightarrow\dfrac{14m-2m^2}{2}-\dfrac{43}{2}=0\)

pt vô nghiệm

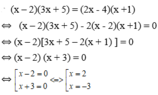
Vậy phương trình đã cho có tập nghiệm là S ={-3; 2}

1) \(\left(2x+5\right)\left(x-4\right)=\left(x-5\right)\left(4-x\right)\)

\(\Leftrightarrow\left(2x+5\right)\left(x-4\right)+\left(x-4\right)\left(x-5\right)=0\)

\(\Leftrightarrow\left(x-4\right)\cdot3x=0\)

\(\Leftrightarrow\orbr{\begin{cases}x=4\\x=0\end{cases}}\)

2) \(9x^2-1=3x+1\)

\(\Leftrightarrow\left(3x+1\right)\left(3x-1\right)-\left(3x+1\right)=0\)

\(\Leftrightarrow\left(3x+1\right)\left(3x-2\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}x=-\frac{1}{3}\\x=\frac{2}{3}\end{cases}}\)

1/ \(2\left(x-5\right)=\left(-x-5\right)\)

\(\Leftrightarrow2x-10=-x-5\)

\(\Leftrightarrow3x=5\)

\(\Leftrightarrow x=\dfrac{5}{3}\)

Vậy: \(S=\left\{\dfrac{5}{3}\right\}\)

==========

2/ \(2\left(x+3\right)-3\left(x-1\right)=2\)

\(\Leftrightarrow2x+6-3x+3=2\)

\(\Leftrightarrow-x=-7\)

\(\Leftrightarrow x=7\)

Vậy: \(S=\left\{7\right\}\)

==========

3/ \(4\left(x-5\right)-\left(3x-1\right)=x-19\)

\(\Leftrightarrow4x-20-3x+1=x-19\)

\(\Leftrightarrow0x=0\)

Vậy: \(S=\left\{x|x\text{ ∈ }R\right\}\) 

===========

4/ \(7-\left(x-2\right)=5\left(2-3x\right)\)

\(\Leftrightarrow7-x+2=10-15x\)

\(\Leftrightarrow14x=1\)

\(\Leftrightarrow x=\dfrac{1}{14}\)

Vậy: \(S=\left\{\dfrac{1}{14}\right\}\)

==========

5/ \(2x-\left(5-3x\right)=7x+1\)

\(\Leftrightarrow2x-5+3x=7x+1\)

\(\Leftrightarrow-2x=6\)

\(\Leftrightarrow x=-3\)

Vậy: \(S=\left\{-3\right\}\)

[---]

Chúc bạn học tốt.

1. \(2\left(x-5\right)=-x-5\)

\(\Leftrightarrow3x=5\)

\(\Leftrightarrow x=\dfrac{5}{3}\)

Vậy \(S=\left\{\dfrac{5}{3}\right\}\)

2. \(2\left(x+3\right)-3\left(x-1\right)=2\)

\(\Leftrightarrow2x+6-3x+3=2\)

\(\Leftrightarrow x=7\)

Vậy \(S=\left\{7\right\}\)

3. \(4\left(x-5\right)-\left(3x-1\right)=x-19\)

\(\Leftrightarrow4x-20-3x+1-x+19=0\)

\(\Leftrightarrow0x=0\)

Vậy \(S=\left\{x\in R\right\}\)

4. \(7-\left(x-2\right)=5\left(2-3x\right)\)

\(\Leftrightarrow7-x+2-10+15x=0\)

\(\Leftrightarrow14x-1=0\)

\(\Leftrightarrow x=\dfrac{1}{14}\)

Vậy \(S=\left\{\dfrac{1}{14}\right\}\)

4. \(2x-\left(5-3x\right)=7x+1\)

\(\Leftrightarrow2x-5+3x-7x-1=0\)

\(\Leftrightarrow-2x-6=0\)

\(\Leftrightarrow x=-3\)

Vậy \(S=\left\{-3\right\}\)

1: Ta có: \(2\left(x-5\right)=\left(-x-5\right)\)

\(\Leftrightarrow2x-10+x+5=0\)

\(\Leftrightarrow3x=5\)

hay \(x=\dfrac{5}{3}\)

2: Ta có: \(2\left(x+3\right)-3\left(x-1\right)=2\)

\(\Leftrightarrow2x+6-3x+3=2\)

\(\Leftrightarrow-x=-7\)

hay x=7

3: Ta có: \(4\left(x-5\right)-\left(3x-1\right)=x-19\)

\(\Leftrightarrow4x-20-3x+1-x+19=0\)

\(\Leftrightarrow0x=0\)(luôn đúng

1/ \(7x-5=13-5x\)

\(\Leftrightarrow12x=18\)

\(\Leftrightarrow x=\dfrac{3}{2}\)

Vậy: \(S=\left\{\dfrac{3}{2}\right\}\)

==========

2/ \(19+3x=5-18x\)

\(\Leftrightarrow21x=-14\)

\(\Leftrightarrow x=-\dfrac{2}{3}\)

Vậy: \(S=\left\{-\dfrac{2}{3}\right\}\)

==========

3/ \(x^2+2x-4=-12+3x+x^2\)

\(\Leftrightarrow-x=-8\)

\(\Leftrightarrow x=8\)

Vậy: \(S=\left\{8\right\}\)

===========

4/ \(-\left(x+5\right)=3\left(x-5\right)\)

\(\Leftrightarrow-x-5=3x-15\)

\(\Leftrightarrow-4x=-10\)

\(\Leftrightarrow x=\dfrac{5}{2}\)

Vậy: \(S=\left\{\dfrac{5}{2}\right\}\)

==========

5/ \(3\left(x+4\right)=\left(-x+4\right)\)

\(\Leftrightarrow3x+12=-x+4\)

\(\Leftrightarrow4x=-8\)

\(\Leftrightarrow x=-2\)

Vậy: \(S=\left\{-2\right\}\)

[----------]

1. \(7x-5=13-5x\) \(\Leftrightarrow12x=18\Leftrightarrow x=\dfrac{3}{2}\)

2. \(19+3x=5-18x\Leftrightarrow21x=-14\Leftrightarrow x=-\dfrac{2}{3}\)

3. \(x^2+2x-4=-12+3x+x^2\Leftrightarrow-x=-8\Leftrightarrow x=8\)

4. \(-\left(x+5\right)=3\left(x-5\right)\Leftrightarrow-x-5=3x-15\Leftrightarrow4x=10\Leftrightarrow x=\dfrac{5}{2}\)

5. \(3\left(x+4\right)=-x+4\Leftrightarrow3x+12=-x+4\Leftrightarrow4x=-8\Leftrightarrow x=-2\)

1) Ta có: \(7x-5=13-5x\)

\(\Leftrightarrow12x=18\)

hay \(x=\dfrac{3}{2}\)

2) Ta có: \(19+3x=5-18x\)

\(\Leftrightarrow21x=-14\)

hay \(x=-\dfrac{2}{3}\)

3) Ta có: \(x^2+2x-4=x^2+3x-12\)

\(\Leftrightarrow3x-12=2x-4\)

hay x=8

4) Ta có: \(-\left(x+5\right)=3\left(x-5\right)\)

\(\Leftrightarrow-x-5-3x+15=0\)

\(\Leftrightarrow-4x=-10\)

hay \(x=\dfrac{5}{2}\)