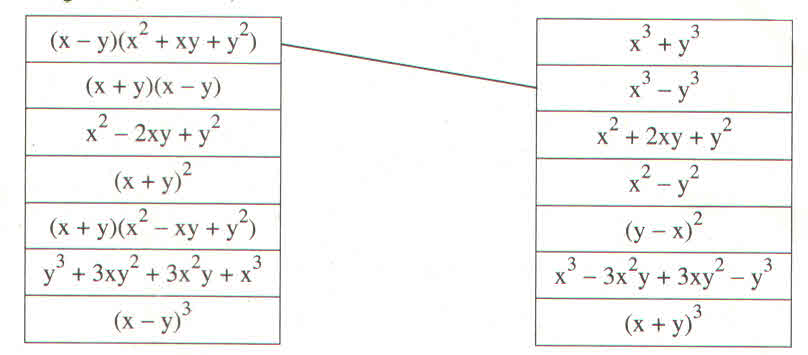
Dùng bút chì nối các biểu thức sao cho chúng tạo thành hai vế của một hằng đẳng thức (theo mẫu):
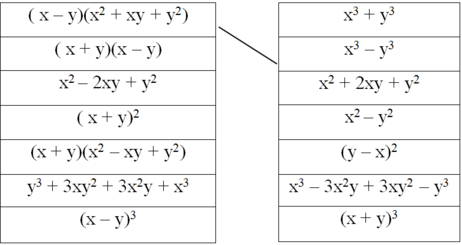
Nối các biểu thức sao cho chúng tạo thành hai vế của một hằng đẳng thức (theo mẫu) :
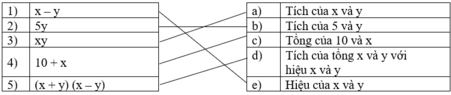
Dùng bút chì nối các ý 1), 2), ..., 5) với a), b), ..., e) sao cho chúng có cùng ý nghĩa (chẳng hạn như nối ý 1) với e)):
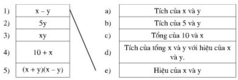
Ý 1) đã cho là x – y được đọc là hiệu của x và y. Đem so sánh với các ý cần nối kết thì ta chọn ý e) vì chúng có cùng ý nghĩa.
Ý 2): Biểu thức 5y được đọc là Tích của 5 và y. Nối 2) với b)
Ý 3): Biểu thức xy được đọc là Tích của x và y. Nối 3) với a)
Ý 4): Biểu thức x + y được đọc là Tổng của 10 và x. Nối 4) với c)
Ý 5): Biểu thức (x + y)(x - y) được đọc là Tích của tổng x và y với hiệu của x và y. Nối 5) với d)
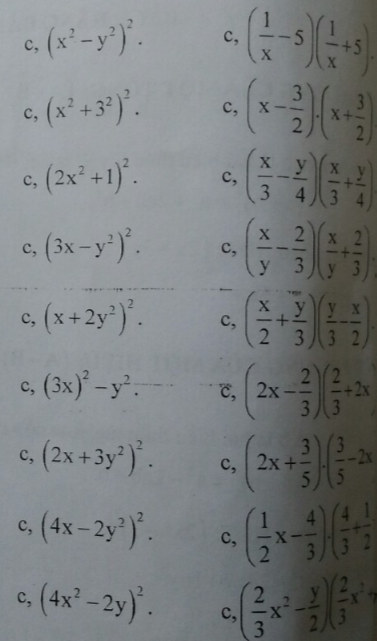 viết lại các đa thức thành các vế kia hằng đẳng thức giúp em với ạ em đang cần gấp
viết lại các đa thức thành các vế kia hằng đẳng thức giúp em với ạ em đang cần gấp
c) \(\left(x^2-y^2\right)^2=x^4-2x^2y^2+y^4\)
c) \(\left(x^2+3^2\right)^2=x^4+18x+81\)
c) \(\left(2x^2+1\right)^2=4x^4+4x^2+1\)
c) \(\left(3x-y^2\right)^2=9x^2-6xy^2+y^4\)
c) \(\left(x+2y^2\right)^2=x^2+4xy^2+4y^4\)
c) \(\left(3x\right)^2-y^2=\left(3x-y\right)\left(3x+y\right)\)
c) \(\left(2x+3y^2\right)^2=4x^2+12xy^2+9y^4\)
c) \(\left(4x-2y^2\right)^2=16x^2-16xy^2+4y^4\)
c) \(\left(4x^2-2y\right)^2=16x^4-16x^2y+4y^2\)
c) \(\left(\dfrac{1}{x}-5\right)\left(\dfrac{1}{x}+5\right)=\dfrac{1}{x^2}-25\)
c) \(\left(x-\dfrac{3}{2}\right)\left(x+\dfrac{3}{2}\right)=x^2-\dfrac{9}{4}\)
c) \(\left(\dfrac{x}{3}-\dfrac{y}{4}\right)\left(\dfrac{x}{3}+\dfrac{y}{4}\right)=\dfrac{x^2}{9}-\dfrac{y^2}{16}\)
c) \(\left(\dfrac{x}{y}-\dfrac{2}{3}\right)\left(\dfrac{x}{y}+\dfrac{2}{3}\right)=\dfrac{x^2}{y^2}-\dfrac{4}{9}\)
c) \(\left(\dfrac{x}{2}+\dfrac{y}{3}\right)\left(\dfrac{y}{3}-\dfrac{x}{2}\right)=\dfrac{y^2}{9}-\dfrac{x^2}{4}\)
c) \(\left(2x-\dfrac{2}{3}\right)\left(\dfrac{2}{3}+2x\right)=4x^2-\dfrac{4}{9}\)
c) \(\left(2x+\dfrac{3}{5}\right)\left(\dfrac{3}{5}-2x\right)=\dfrac{9}{25}-4x^2\)
c) \(\left(\dfrac{1}{2}x-\dfrac{4}{3}\right)\left(\dfrac{4}{4}+\dfrac{1}{2}x\right)=\dfrac{1}{4}x^2-\dfrac{16}{9}\)
c) \(\left(\dfrac{2}{3}x^2-\dfrac{y}{2}\right)\left(\dfrac{2}{3}x^2+\dfrac{y}{2}\right)=\dfrac{4}{9}x^4-\dfrac{y^2}{4}\)
Bổ sung vế còn lại để tạo thành hằng đẳng thức đúng:
(y-5).(y2+5y+25)
\(\left(y-5\right).\left(y^2+5y+25\right)=y^3-5^3=y^3-125\)
Dùng bút chì vẽ đường nối các điểm giao nhau giữa các gợn lồi hoặc của các gợn lõm của hai nguồn sóng trên Hình 3.6 và đối chiếu kết quả với công thức (3.1).
\(x_1-x_2=k\lambda\) (k là số nguyên) (3.1)
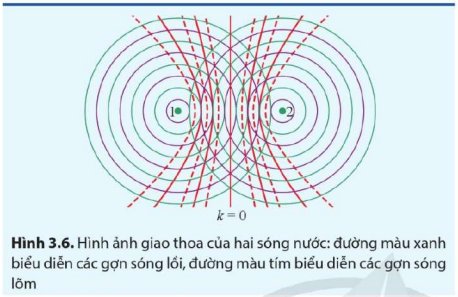
Nối các điểm giao nhau giữa các gợn lồi hoặc của các gợn lõm của hai nguồn sóng với mỗi nguồn, đo khoảng cách \(x_1,x_2\). Tính \(\dfrac{x_1-x_2}{\lambda}\) với \(\lambda\) được xác định trong câu hỏi trước. Nếu thương số nhận được là một số nguyên thì kết quả đúng với công thức.
RÚT GỌN CÁC BIỂU THỨC SAU:
Gợi ý: Dùng hằng đẳng thức để rút gọn nhanh hơn (nhưng cũng phải biến đổi rõ ràng ra rồi mới ra hằng đẳng thức chứ ko đc làm nhanh bằng cách ghi hằng đẳng thức ngay!)
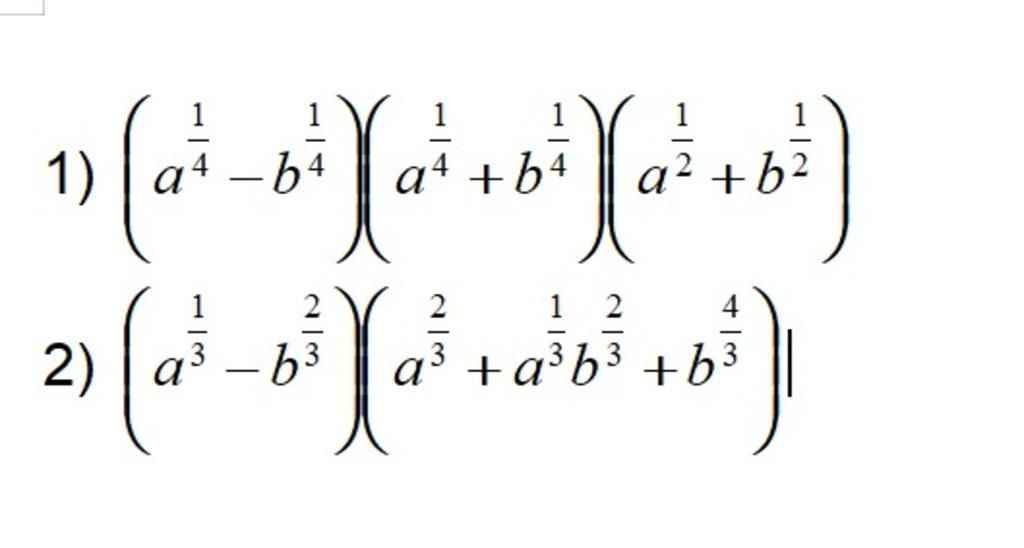
`1)(a^[1/4]-b^[1/4])(a^[1/4]+b^[1/4])(a^[1/2]+b^[1/2])`
`=[(a^[1/4])^2-(b^[1/4])^2](a^[1/2]+b^[1/2])`
`=(a^[1/2]-b^[1/2])(a^[1/2]+b^[1/2])`
`=a-b`
`2)(a^[1/3]-b^[2/3])(a^[2/3]+a^[1/3]b^[2/3]+b^[4/3])`
`=(a^[1/3]-b^[2/3])[(a^[1/3])^2+a^[1/3]b^[2/3]+(b^[2/3])^2]`
`=(a^[1/3])^3-(b^[2/3])^3`
`=a-b^2`
các ơi cho mình hỏi trong các hằng đẳng thức có hiệu của hai bình phương nhưng tại sao lại không có tổng của hai bình phương? tổng của hai bình phương là hằng đẳng thức như thế nào?
x^2 + y^2 = (x + y +\(\sqrt{2xy}\))(x + y - \(\sqrt{2xy}\))
xét hằng đẳng thức (x+1)^4=x^4+4x^3+6x^2+4x+1. Lần lượt cho x bằng 1,2,...,n rồi cộng từng vế n đẳng thức trên để tính giá trị của biểu thức: S=1^3+2^3+...+n^3.
S=n(n+1)mũ 2 trên 4
Xét hằng đẳng thức: (x+1)^2 = x^2 +2x +1
Lần lượt cho x bằng 1;2;3;...;n rồi cộng từng vế n đẳng thức trên để tính giá trị của biểu thức S3= 1^3 + 2^3 + 3^3 +...+n^3