Hình bên dưới, cho ABCD là hình bình hành. Chứng minh rằng AE //CF.
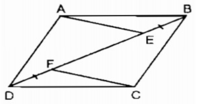
Cho hình bình hành ABCD. Từ A và C kẻ AE vuông góc với BD, CF vuông góc với BD. Chứng minh rằng AE, CF là hình bình hành.
Vì ABCD là hình bình hành
=> + AB = DC
AB // DC => góc ABE = góc FCD ( sole trong )
+ AD= BC
AD // BC
+) Xét \(\Delta AEB\)và \(\Delta CFD\)có :
\(AB=CD\left(cmt\right)\)
\(\widehat{AEB}=\widehat{CFD}=90^o\)(gt )
\(\widehat{ABE}=\widehat{FCD}\)(cmt)
Do đó : tam giác vuông AEB = tam giác vuông CFD ( cạnh huyền - góc nhọn )
\(\Rightarrow AE=FC\)( cặp cạnh tương ứng ) (1)
+) vÌ \(\hept{\begin{cases}AE\perp DB\\FC\perp DB\end{cases}}\)
=> AE // FC (2)
Từ (1) và (2)
=> AECF là hình bình hành ( đpcm )
cho hình bình hành ABCD gọi E,F,G,H lần luợt là điểm thuộc AB,CD,BC,AD sao cho AE=CF,BG=DH chứng minh rằng tứ giác EGFH là hình bình hành( vẽ hình) giúp vs ạ
Ta có: AE+EB=AB
CF+FD=CD
mà AB=CD
và AE=CF
nên EB=FD
Ta có: AH+HD=AD
CG+BG=CB
mà AD=CB
và HD=BG
nên AH=CG
Xét ΔAHE và ΔCGF có
AH=CG
\(\widehat{A}=\widehat{C}\)
AE=CF
Do đó: ΔAHE=ΔCGF
Suy ra: HE=GF
Xét ΔEBG và ΔFDH có
EB=FD
\(\widehat{B}=\widehat{D}\)
BG=DH
Do đó: ΔEBG=ΔFDH
Suy ra: EG=FH
Xét tứ giác EHFG có
EG=FH
EH=FG
Do đó: EHFG là hình bình hành
Cho hình bình hành ABCD. Gọi E, F lần lượt là hình chiếu của A, C trên BD. a) Chứng minh: AE = CF b) Chứng minh AECF là hình bình hành
a: Xét ΔADE vuông tại E và ΔCBF vuông tại F có
AD=CB
\(\widehat{ADE}=\widehat{CBF}\)
Do đó: ΔADE=ΔCBF
Suy ra: AE=CF
b: Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
Cho hình bình hành ABCD. Trên các cạnh AB và BC của hình bình hành ABCD, lần lượt lấy các điểm E và F sao cho AE = CF. AF cắt CE tại P. Chứng minh rằng DP là tia phân giác của ADC
*AF cắt DC tại G.
-△APE có: AE//CG (ABCD là hình bình hành) \(\Rightarrow\dfrac{AP}{PG}=\dfrac{AE}{CG}\) (hệ quả định lý Ta-let) mà \(AE=CF\left(gt\right)\) \(\Rightarrow\dfrac{AP}{PG}=\dfrac{CF}{CG}\)
-△ADG có: CF//AD (ABCD là hình bình hành) \(\Rightarrow\dfrac{CF}{AD}=\dfrac{CG}{DG}\Rightarrow\dfrac{AD}{DG}=\dfrac{CF}{CG}=\dfrac{AP}{PG}\)
*AH//DP (H thuộc DC)
△AHG có: AH//DP (gt) \(\Rightarrow\dfrac{AP}{PG}=\dfrac{DH}{DG}=\dfrac{AD}{DG}\Rightarrow DH=AD\)
\(\Rightarrow\)△ADH cân tại D. \(\Rightarrow\widehat{HAD}=\widehat{ADH}=\widehat{ADP}=\widehat{CDP}\)
\(\Rightarrow\)DP là tia phân giác của góc ADC
Làm giúp mình với ạ mình cần tối nay ạ
Cho hình bình hành ABCD, E, F thuộc đường chéo BD, sao cho BE = DF
a/ Chứng minh AE // CF
b/ AE cắt BC tại K, CF cắt AD tại I. Chứng minh tứ giác AKCI là hình bình hành
a: Xét ΔAEB và ΔCFD có
AB=CD
\(\widehat{ABE}=\widehat{CDF}\)
BE=DF
Do đó: ΔAEB=ΔCFD
Suy ra: \(\widehat{AEB}=\widehat{CFD}\)
\(\Leftrightarrow\widehat{AEF}=\widehat{EFC}\)
mà hai góc này là hai góc ở vị trí đồng vị
nên AE//CF
Cho hình bình hành ABCD . Trên cạnh AB lấy điểm E , trên cạnh CD lấy điểm F sao cho AE = CF. a / Chứng minh DE = BF b / Chứng minh tứ giác AECF là hình bình hành . c / Chứng minh tứ giác BEDF là hình bình hành
a: Ta có: AE+EB=AB
DF+FC=DC
mà AE=FC
và AB=DC
nên EB=DF
Xét tứ giác EBFD có
EB//DF
EB=DF
Do đó: EBFD là hình bình hành
Suy ra: DE=BF
b: Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
Cho hình bình hành ABCD. Trêb AD, BC lấy AE=CF. Trên AB,CD lấy BM=ND. Chứng minh EACF, DMBN là hình bình hành
Hình bên cho ABCD là hình bình hành. Chứng minh rằng AECF là hình bình hành.
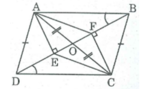
Gọi O là'giao điểm của AC và BD, ta có:
OA = OC (tính chất hình bình hành) (1)
Xét hai tam giác vuông AEO và CFO, ta có:
∠ (AEO) = ∠ (CFO) = 90 0
OA = OC (chứng minh trên)
∠ (AOE) = ∠ (COF) (đối đỉnh)
Do đó ∆ AEO = ∆ CFO (cạnh huyền, góc nhọn)
⇒ OE = OF (2)
Từ (1) và (2) suy ra tứ giác AECF là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường).
Hình 10
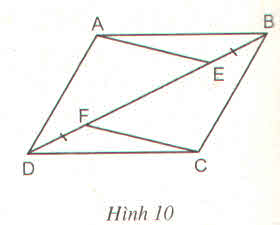
Cho ABCD là hình bình hành. Chứng minh rằng AE // CF ?
Gọi O là giao điểm của AC và BD. Ta có OA = OC, OE = OF nên AECF là hình bình hành. Suy ra AE // CF.
Gọi O là giao điểm của AC và BD, ta có:
(tính chất hình bình hành)
Xét ∆ AEB và ∆ CFD :
AB = CD (tính chất hình bình hành)
ˆABE=ˆCDFABE^=CDF^ (so le trong)
BE = DF (gt)
Do đó: ∆ AEB = ∆ CFD (c.g.c)
⇒ BE = DF
Ta có: OB = OE + BE
OD = OF + DF
Suy ra: OE = OF
Suy ra: Tứ giác AECF là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường) // CF