Cho mệnh đề chứa biến P ( x ) : " x ∈ ℝ : x + 8 ≤ x 2 " . Mệnh đề đúng là:
A. P(-2)
B. P(0)
C. P(3)
D. P(5)
Những câu hỏi liên quan
Cho các tập hợp:
M
{
x
∈
ℝ
:
x
≥
−
3
}
,
N
{
x
∈
ℝ
:
−
2
≤
x
≤
1
}
,
P
{
x
∈
ℝ
:
−
5
x
≤
0
}
.Mệnh đề nào sau đây là mệnh đề đúng? A.
M
⊂
N
B.
M
⊃
P
C. ...
Đọc tiếp
Cho các tập hợp:
M = { x ∈ ℝ : x ≥ − 3 } , N = { x ∈ ℝ : − 2 ≤ x ≤ 1 } , P = { x ∈ ℝ : − 5 < x ≤ 0 } .
Mệnh đề nào sau đây là mệnh đề đúng?
A. M ⊂ N
B. M ⊃ P
C. N ⊂ M
D. N ⊂ P
Đáp án C.
Giải thích
M = x ∈ R : x ≥ - 3 = [ - 3 ; + ∞ ) N = x ∈ R : - 2 ≤ x ≤ 1 = [ - 2 ; 1 ] P = x ∈ R : - 5 < x ≤ 0 = ( - 5 ; 0 ]
Ta thấy rằng - 2 ; 1 ⊂ [ - 3 ; + ∞ ) d o đ ó N ⊂ M
Đúng 0
Bình luận (0)
Cho mệnh đề chứa biến: 3-2x > 3x-83−2x>3x−8. Tìm hai giá trị nguyên a,a, bb thuộc khoảng (-10;10)(−10;10) sao cho x = ax=a thì mệnh đề đúng, x= bx=b thì mệnh đề sai.
Cho hàm số f(x) xác định, liên tục trên ℝ và có bảng biến thiên như sau:Mệnh đề nào dưới đây là mệnh đề đúng? A. Hàm số có giá trị cực đại bằng 3. B. Hàm số có hai điểm cực trị. C. Hàm số có giá trị lớn nhất bằng 1, nhỏ nhất bằng -1/3. D. Đồ thị hàm số không cắt trục hoành.
Đọc tiếp
Cho hàm số f(x) xác định, liên tục trên ℝ và có bảng biến thiên như sau:
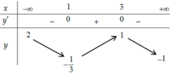
Mệnh đề nào dưới đây là mệnh đề đúng?
A. Hàm số có giá trị cực đại bằng 3.
B. Hàm số có hai điểm cực trị.
C. Hàm số có giá trị lớn nhất bằng 1, nhỏ nhất bằng -1/3.
D. Đồ thị hàm số không cắt trục hoành.
Cho mệnh đề chứa biến: 2-3x > x-192−3x>x−19. Tìm hai giá trị nguyên a,a, bb thuộc khoảng (-10;10)(−10;10) sao cho x = ax=a thì mệnh đề đúng, x= bx=b thì mệnh đề sai.
Với mỗi mệnh đề chứa biến sau, tìm những giá trị của biến để nhận được một mệnh đề đúng và một mệnh đề sai.
a) \(P(x): "x^2=2"\)
b) \(Q(x): "x^2+1>0"\)
c) \(R(n): "n+2\) chia hết cho 3” (n là số tự nhiên).
a)
+) \(x = \sqrt 2 \) ta được mệnh đề là một mệnh đề đúng.
+) \(x = 0\) ta được mệnh đề là một mệnh đề sai.
b)
+) \(x = 0\) ta được mệnh đề là một mệnh đề đúng.
+) Không có giá trị của x để là một mệnh đề sai do \({x^2} + 1 > 0\) với mọi x.
c) chia hết cho 3” (n là số tự nhiên).
+) \(n = 1\) ta được mệnh đề chia hết cho 3” là một mệnh đề đúng.
+) \(n = 5\)ta được mệnh đề chia hết cho 3” là một mệnh đề sai.
Đúng 0
Bình luận (0)
Cho mệnh đề chứa biến P(x): “ x + 12 > x2”. Mệnh đề nào sau đây đúng?
A. P(3).
B. P(5).
C. P(4).
D. P(9).
Đáp án: A
A. 3 +12 = 15 > 32 => mệnh đề đúng.
B. 5 +12 = 17 < 52 => mệnh đề sai.
C. 4 +12 = 16 = 42 => mệnh đề sai.
D. 9 +12 = 21 < 92 => mệnh đề sai.
Đúng 0
Bình luận (0)
giúp mk vs mk cần gấp cho tối nay, giải từng bước mk đc ko
Với giá trị nào của x thì mệnh đề chứa biến:"\(x^2\) - 8 > 4x" trở thành mệnh đề đúng?
A. x= -1 B. x=3 C. x=6 D. x=0
Bạn thay giá trị $x$ của từng đáp án vô xem $x^2-8$ có lớn hơn $4x$ không thì đáp án đó đúng
Đáp án $x=6$ (C)
Đúng 1
Bình luận (1)
Cho mênh đề “
∀
x
∈
ℝ
,
x
2
+
x
≥
−
1
4
”. Lập mệnh đề phủ định của mệnh đề A và xét tính đúng sai của nó A.
A
¯
:
∃
x
∈
ℝ
,
x
2
+
x
≥
−
1
4...
Đọc tiếp
Cho mênh đề “ ∀ x ∈ ℝ , x 2 + x ≥ − 1 4 ”. Lập mệnh đề phủ định của mệnh đề A và xét tính đúng sai của nó
A. A ¯ : " ∃ x ∈ ℝ , x 2 + x ≥ − 1 4 " Đây là mệnh đề đúng
B. A ¯ : " ∃ x ∈ ℝ , x 2 + x ≤ − 1 4 " Đây là mệnh đề đúng
C. A ¯ : " ∃ x ∈ ℝ , x 2 + x < − 1 4 " Đây là mệnh đề đúng
D. A ¯ : " ∃ x ∈ ℝ , x 2 + x ≥ − 1 4 " Đây là mệnh đề sai
cho mệnh đề chứa biến ''x2 - 3x +2 >0'' Hãy xác định tính đúng sai của các mệnh đề có được khi cho biến x nhận các giá trị sau đây a) x= 2 b) x= 0 c) x= 0,5 d) x= -1
