Cho hàm số f x = x 2 + mx , khi x ≤ 1 x + 3 − 2 x − 1 , khi x > 1 . Tìm m đề hàm số đã cho liên tục tại x = 1 .
A. − 3 4
B. 2
C. 3 4
D. 1 3
Cho hàm số y=f(x) có đạo hàm f'(x)= x ( x - 1 ) 2 ( x 2 + m x + 9 ) . Có bao nhiêu số nguyên dương m để hàm số y=f(3-x) đồng biến trên khoảng ( 3 ; + ∞ ) .
A. 6.
B. 8.
C. 5.
D. 7.
Cho hàm số y=f(x) liên tục và có đạo hàm trên R. Biết hàm số f’(x) có đồ thị được cho trong hình vẽ. Tìm điều kiện của m để hàm số g(x)=f(2019)x – mx +2 đồng biến trên [0;1]
![]()
![]()
![]()
![]()
Cho hàm số f(x) = mx^2 +2x +2 khi x>0 và nx +2 khi x<=0. Tìm tất cả các giá trị của các tham số m,n sao cho f(x) có đạo hàm tại x=0
Để hàm số có đạo hàm tại x=0 phải thỏa mãn 2 điều kiện, đó là hàm số liên tục tại x=0 và có đạo hàm bên trái bằng đạo hàm bên phải
Để hàm số liên tục tại x=0 \(\Leftrightarrow\lim\limits_{x\rightarrow0^+}=\lim\limits_{x\rightarrow0^-}=f\left(0\right)\Leftrightarrow2=2\left(tm\right)\)
\(f'\left(0^+\right)=\lim\limits_{x\rightarrow0^+}\dfrac{f\left(x\right)-f\left(0\right)}{x-0}=\lim\limits_{x\rightarrow0^+}\dfrac{mx^2+2x+2-2}{x}=\lim\limits_{x\rightarrow0^+}\dfrac{x\left(mx+2\right)}{x}=2\)
\(f'\left(0^-\right)=\lim\limits_{x\rightarrow0^-}\dfrac{f\left(x\right)-f\left(0\right)}{x-0}=\lim\limits_{x\rightarrow0^-}\dfrac{nx+2-2}{x}=n\)
\(\Rightarrow\left\{{}\begin{matrix}m\in R\\n=2\end{matrix}\right.\)
\(f\left(0^+\right)=f\left(0^-\right)\Leftrightarrow n=2\)
Cho hàm số y=f(x)=√x+7 -3∠x-2 , xkhác 2 ; mx+2023 ,x=2 (với m là tham số)
Tìm m để hàm số liên tục tại điểm x=2
\(f\left(x\right)=\left\{{}\begin{matrix}\dfrac{\sqrt{x+7}-3}{x-2}\left(x< >2\right)\\mx+2023\left(x=2\right)\end{matrix}\right.\)
Để hàm số liên tục tại x=2 thì \(\lim\limits_{x\rightarrow2}f\left(x\right)=F\left(2\right)\)
=>\(\lim\limits_{x\rightarrow2}\dfrac{x+7-9}{\left(x-2\right)\left(\sqrt{x+7}+3\right)}=2m+2023\)
=>\(2m+2023=\dfrac{1}{\sqrt{2+7}+3}=\dfrac{1}{6}\)
=>m=-12137/12
Cho hàm số y = f(x) = 2 x + m x - 1 . Tính tổng các giá trị của tham số m để m a x [ 2 ; 3 ] f ( x ) - m i n [ 2 ; 3 ] f ( x ) = 2.
A. -4
B. -2
C. -1
D. -3
Chọn A
Hàm số y = f(x) = 2 x + m x - 1 . xác định và liên tục trên [2;3].
Với m = -2, hàm số trở thành y = 2![]() (không thỏa)
(không thỏa)
Với ![]() ta có:
ta có: 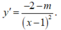
Khi đó hàm số luôn đồng biến hoặc nghịch biến trên [2;3]
Suy ra 
Do đó: ![]()
![]()
Theo giả thiết ![]()
![]()
Vậy tổng các giá trị của tham số thỏa mãn yêu cầu bài toán là: -4.
Nhận xét: đề bài cho thêm dấu giá trị tuyệt đối ở trong biểu thức ![]() là không cần thiết.
là không cần thiết.
Cho hàm số y = f(x) = 2 x + m x - 1 . Tính tổng các giá trị của tham số m để m a x [ 2 ; 3 ] f ( x ) - m i n [ 2 ; 3 ] f ( x ) = 2
A. -4
B. -2
C. -1
D. -3
Chọn A
Hàm số y = f(x) =
2
x
+
m
x
-
1
xác định và liên tục trên [2;3]
Với m = -2, hàm số trở thành y = 2 ![]() (không thỏa).
(không thỏa).
Với m
≠
2, ta có: 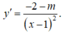
Khi đó hàm số luôn đồng biến hoặc nghịch biến trên [2;3]
Suy ra

Do đó:
![]()
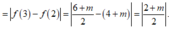
Theo giả thiết
![]()
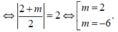
Vậy tổng các giá trị của tham số thỏa mãn yêu cầu bài toán là: -4.
Nhận xét: đề bài cho thêm dấu giá trị tuyệt đối ở trong biểu thức ![]() là không cần thiết.
là không cần thiết.
1/ Cho hàm số \(f\)(\(x\))=\(\dfrac{1}{3}\)\(x\)\(^3\)+\(x \)\(^2\)-(\(m\)+1)\(x\)-\(m\)+3. Với \(m\) là tham số. Có bao nhiêu số nguyên \(m\) thuộc đoạn [-10;10] để \(f\)'(\(x\)) ≥ 0, ∀\(x\) ϵ \(R\)
2/ Cho hàm số \(y\) = \(\dfrac{mx+4}{x+m}\). Với \(m\) là tham số. Có bao nhiêu số nguyên m thuộc đoạn [-5;2023] để \(y\)' > 0, ∀\(x\) ϵ (0;+∞).
1: \(f'\left(x\right)=\dfrac{1}{3}\cdot3x^2+2x-\left(m+1\right)=x^2+2x-m-1\)
\(\Delta=2^2-4\left(-m-1\right)=4m+8\)
Để f'(x)>=0 với mọi x thì 4m+8<=0 và 1>0
=>m<=-2
=>\(m\in\left\{-10;-9;...;-2\right\}\)
=>Có 9 số
Cho hàm số \(f\left(x\right)=x^4-\left(m+2\right)x^3+mx+3\). Trong trường hợp giá trị lớn nhất của hàm số đạt giá trị lớn nhất, tính f(3)
Cho hàm số y=f(x) có đạo hàm f'(x)= x 2 ( x + 1 ) ( x 2 - m x + 16 ) . Có bao nhiêu số nguyên m<100 để hàm số y = f ( x 2 ) có 5 điểm cực trị.
A. 8.
B. 90.
C. 91.
D. 7.
Cho hàm số f ( x ) = 2 x 2 + 3 x - 2 x + 2 k h i x ≠ - 2 m 2 + m x - 8 k h i x = - 2
Tính tổng các giá trị tìm được của tham số m để hàm số liên tục tại x=-2
A.2
B.4
C.1
D.5