Cho a O b ^ = 90 0 . Bên trong a O b ^ vẽ các tia Oc tạo với Oa một góc 30 ° , tia Od tạo với Ob một góc 30 ° . Hãy chỉ ra những tia là tia phân giác.
Những câu hỏi liên quan
cho góc tù xOy. bên trong xOy vẽ tia Om và On sao chớ:xOm=900,yOn=900
a) chung to xOn=yOm
b) gọi Ot là tia nằm trong xOy sao cho:xOt=tOy. chứng minh Ot là tia phân giác của góc mOn
bạn phải vẽ hình ra thì bọn mình mới giúp cho được chứ
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho hình vẽ bên : biết a song song với b, ^{^◻ĐAB}90^0;^{^◻BCD130^0}Tính ^{^◻Đ_1};^{^◻B_1} ?
Đọc tiếp
Cho hình vẽ bên :
biết a song song với b, \(^{^◻ĐAB}\)=90\(^0\);\(^{^◻BCD=130^0}\)
Tính \(^{^◻Đ_1}\);\(^{^◻B_1}\)= ?
Cho hình vẽ bên : biết a song song với b, ^{^◻ĐAB90^0};^{^◻BCD130^0}Tính ^{^◻Đ_1};^{^◻B_1} ?Mình cần gấp ạ!
Đọc tiếp
Cho hình vẽ bên :
biết a song song với b, \(^{^◻ĐAB=90^0}\);\(^{^◻BCD=130^0}\)
Tính \(^{^◻Đ_1}\);\(^{^◻B_1}\)= ?
Mình cần gấp ạ!
Do a//b \(\Rightarrow\widehat{DAB}+\widehat{B_1}=180^o\)(2 góc tcp)
\(\Rightarrow90^o+\widehat{B_1}=180^o\)
\(\Rightarrow\widehat{B_1}=180^o-90^o=90^o\)
Do a// b \(\Rightarrow\widehat{BCD}+\widehat{D_1}=180^o\)
\(\Rightarrow130^o+\widehat{D_1}=180^o\)
\(\Rightarrow\widehat{D_1}=180^o-130^o=50^o\)
Đúng 1
Bình luận (0)
4 tháng 10 2021 lúc 15:25
a b A B C O D cho A_140^0,B^150^0,AOB90^0a)CHỨNG MINH a//b b)TÍNH CDBGiups mk nhá
Đọc tiếp
cho \(A_1\)=\(40^0,B^1=50^0,AOB=90^0\)
a)CHỨNG MINH a//b
b)TÍNH CDB
Giups mk nhá 
Xét tính đúng - sai của mỗi khẳng định sau :
Cho tam giác ABC nội tiếp đường tròn (O)
a) Nếu BC là đường kính của đường tròn thì \(\widehat{BAC}=90^0\)
b) Nếu AB = AC thì AO vuông góc với BC
c) Nếu tam giác ABC không vuông thì điểm O nằm bên trong tam giác đó
Cho ∠xOy = 90◦. a) Dựng tia Oz nằm giữa hai tia Ox, Oy sao cho ∠xOz = 30◦. b) Trên tia Ox,Oz lần lượt lấy các điểm A,B sao cho OA = OB (A,B ̸= O). Dựng về phía bên trong tam giác OAB tam giác đều ABC. Đường thẳng AC cắt Oy tại D. Chứng minh rằng C là trung điểm của AD. c) Chứng minh rằng đường trung trực của các đoạn thẳng CO,CB và tia Oy đồng quy. Giúp nình vơi!!
a) Nêu nhận xét về vị trí điểm M trên nửa đường tròn đơn vị trong mỗi trường hợp sau:
\(\begin{array}{l}\alpha = {90^o};\\\alpha < {90^o};\\\alpha > {90^o}.\end{array}\)
b) Khi \({0^o} < \alpha < {90^o}\), nêu mối quan hệ giữa \(\cos \alpha ,\;\sin \alpha \) với hoành độ và tung độ của điểm M.
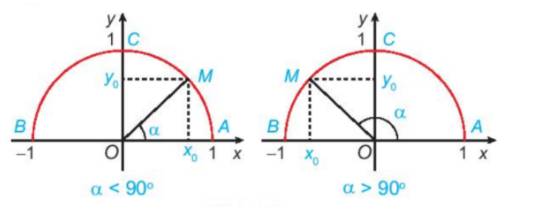
a) Khi \(\alpha = {90^o}\), điểm M trùng với điểm C. (Vì \(\widehat {xOC} = \widehat {AOC} = {90^o}\))
Khi \(\alpha < {90^o}\), điểm M thuộc vào cung AC (bên phải trục tung)
Khi \(\alpha > {90^o}\), điểm M thuộc vào cung BC (bên trái trục tung)
b) Khi \({0^o} < \alpha < {90^o}\) , ta có:
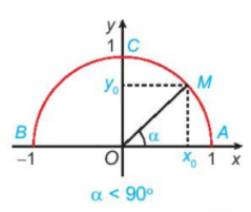
\(\begin{array}{l}\cos \alpha = \frac{{\left| {{x_0}} \right|}}{{OM}} = \left| {{x_0}} \right| = {x_0};\\\sin \alpha = \frac{{\left| {{y_0}} \right|}}{{OM}} = \left| {{y_o}} \right| = {y_o}\end{array}\)
Vì \(OM = R = 1\); \({x_0} \in \)tia \(Ox\)nên \({x_0} > 0\); \({y_0} \in \)tia \(Oy\)nên \({y_0} > 0\)
Vậy \(\cos \alpha \) là hoành độ \({x_0}\)của điểm M, \(\sin \alpha \) là tung độ \({y_0}\) của điểm M.
Đúng 0
Bình luận (0)
Cho đường tròn (O) và điểm M nằm bên ngoài đường tròn . Qua M vẽ hai tiếp tuyến MA , MB với đường tròn (O) trong đó A , B là hai tiếp điểm sao cho AMB = 90 độ . Qua điểm C trên cung nhỏ AB kẻ tiếp tuyến với đường tròn (o) cắt MA , MB tại P vs Q .
CMR : 1/3 ( MA + MB ) < PQ < 1/2 ( MA + MB)
o l m . v n
Cho góc tù xOy. Bên trong góc xOy, vẽ tia Om sao cho góc xOm bằng 900 và vẽ tia On sao cho góc yOn bằng 900.
a. Chứng minh: \(\widehat{xOn}=\widehat{yOm}\).
b. Gọi Ot là tia phân giác của góc xOy. Chứng minh Ot cũng là tia phân giác của góc mOn.
(a) Do tia On nằm giữa 2 tia Ox và Oy nên ta có \(\widehat{xOy}=\widehat{xOn}+\widehat{nOy}\)
\(\Rightarrow\widehat{xOn}=\widehat{xOy}-90^0\) hay \(\widehat{xOn}\) nhọn
\(\Rightarrow\widehat{xOn}< \widehat{xOm}\) mà 2 tia Om và On cùng thuộc nửa mặt phẳng bờ Ox chứa Oy nên tia On nằm giữa tia Ox và tia Oy
\(\Rightarrow\widehat{xOn}+\widehat{mOn}=\widehat{xOm}=90^0\)
Tương tự ta có \(\widehat{yOm}+\widehat{mOn}= 90^0 \). Do đó \(\widehat{xOn}=\widehat{yOm}\) (đpcm).
(b) Ta có: \(\widehat{xOn}=\widehat{xOy}-90^0=\dfrac{1}{2}\widehat{xOy}+\dfrac{\widehat{xOy}-180^0}{2}<\dfrac{\widehat{xOy}}{2}=\widehat{xOt}<90^0=\widehat{xOm}\)Mà Om, On, Ot cùng thuộc nửa mặt phẳng bờ Ox chứa Oy nên tia Ot nằm giữa 2 tia Om và On.
\(\Rightarrow\) \(\widehat{nOt}=\widehat{xOt}-\widehat{xOn}=\widehat{yOt}-\widehat{yOm}=\widehat{tOm}\) hay Ot là phân giác \(\widehat{mOn}\) (đpcm).
Đúng 0
Bình luận (3)
Cho góc tù xOy. Bên trong góc xOy, vẽ tia Om sao cho góc xOm bằng 900 và vẽ tia On sao cho góc yOn bằng 900
a) Chứng minh góc xOn bằng góc yOm
b) Gọi Ot là tia phân giác của góc xOy. Chứng minh Ot cũng là tia phân giác của góc mOn
a) CMR \(\widehat{xOn}\)=\(\widehat{yOm}\)
Ta có
\(\widehat{xOn}\)và\(\widehat{yOm}\)bằng nhau vì chúng có số đo là 900 .Chúng cùng nằm trong \(\widehat{xOy}\)
b) Gọi Ot là tia phân giác của góc \(\widehat{xOy}\). CMR Ot là tia phân giác của \(\widehat{mOn}\)
Vì:
Tia Ot là tia phân giác của \(\widehat{xOy}\)nên ta có:
\(\widehat{xOt}\)+\(\widehat{tOy}\)=\(\widehat{xOy}\)
mà 2 góc \(\widehat{xOn}\)và\(\widehat{yOm}\)tạo thành một góc ở giữa là \(\widehat{mOn}\)nên suy ra Ot cũng là tia phân giác của \(\widehat{mOn}\)
Đúng 0
Bình luận (0)