Cho hai hàm số: f ( x ) = 1 3 x 3 - m + 1 x 2 + m 2 + 2 m + 5 x - 2019 và g ( x ) = ( m 2 + 2 m + 3 ) x 3 - ( 3 m 2 + 6 m + 8 ) x 2 - 4 x + 3 với m là tham số.
Phương trình g(f(x)) = 0 có bao nhiêu nghiệm?
A. 9
B. 6
C. 3
D. 1
1. Cho hàm số \(y=x^3-3mx^2+3\left(2m-1\right)x+1\) . Với giá trị nào của m thì \(f'\left(x\right)-6x>0\) với mọi x>2
A. m > 1/2 B. m < -1/2 C. m >1 D. m ≤ 0
2. Cho hai hàm số f(x) và g(x) đều có đạo hàm trên R và thỏa mãn :
\(f^3\left(2-x\right)-2f^2\left(2+3x\right)+x^2g\left(x\right)+36x=0\) với mọi x thuộc R.
Tính \(A=3f\left(2\right)+4f'\left(2\right)\)
3. Biết hàm số f(x) - f(2x) có đạo hàm bằng 18 tại x=1 và đạo hàm bằng 2000 tại x=2. Tính đạo hàm của hàm số f(x) - f(4x) tại x=1
1.
\(f'\left(x\right)=3x^2-6mx+3\left(2m-1\right)\)
\(f'\left(x\right)-6x=3x^2-3.2\left(m+1\right)x+3\left(2m-1\right)>0\)
\(\Leftrightarrow x^2-2\left(m+1\right)x+2m-1>0\)
\(\Leftrightarrow x^2-2x-1>2m\left(x-1\right)\)
Do \(x>2\Rightarrow x-1>0\) nên BPT tương đương:
\(\dfrac{x^2-2x-1}{x-1}>2m\Leftrightarrow\dfrac{\left(x-1\right)^2-2}{x-1}>2m\)
Đặt \(t=x-1>1\Rightarrow\dfrac{t^2-2}{t}>2m\Leftrightarrow f\left(t\right)=t-\dfrac{2}{t}>2m\)
Xét hàm \(f\left(t\right)\) với \(t>1\) : \(f'\left(t\right)=1+\dfrac{2}{t^2}>0\) ; \(\forall t\Rightarrow f\left(t\right)\) đồng biến
\(\Rightarrow f\left(t\right)>f\left(1\right)=-1\Rightarrow\) BPT đúng với mọi \(t>1\) khi \(2m< -1\Rightarrow m< -\dfrac{1}{2}\)
2.
Thay \(x=0\) vào giả thiết:
\(f^3\left(2\right)-2f^2\left(2\right)=0\Leftrightarrow f^2\left(2\right)\left[f\left(2\right)-2\right]=0\Rightarrow\left[{}\begin{matrix}f\left(2\right)=0\\f\left(2\right)=2\end{matrix}\right.\)
Đạo hàm 2 vế giả thiết:
\(-3f^2\left(2-x\right).f'\left(2-x\right)-12f\left(2+3x\right).f'\left(2+3x\right)+2x.g\left(x\right)+x^2.g'\left(x\right)+36=0\) (1)
Thế \(x=0\) vào (1) ta được:
\(-3f^2\left(2\right).f'\left(2\right)-12f\left(2\right).f'\left(2\right)+36=0\)
\(\Leftrightarrow f^2\left(2\right).f'\left(2\right)+4f\left(2\right).f'\left(2\right)-12=0\) (2)
Với \(f\left(2\right)=0\) thế vào (2) \(\Rightarrow-12=0\) ko thỏa mãn (loại)
\(\Rightarrow f\left(2\right)=2\)
Thế vào (2):
\(4f'\left(2\right)+8f'\left(2\right)-12=0\Leftrightarrow f'\left(2\right)=1\)
\(\Rightarrow A=3.2+4.1\)
3.
Đặt \(g\left(x\right)=f\left(x\right)-f\left(2x\right)\)
\(\Rightarrow g'\left(x\right)=f'\left(x\right)-2f'\left(2x\right)\)
Thay \(x=1\Rightarrow18=f'\left(1\right)-2f'\left(2\right)\) (1)
Thay \(x=2\Rightarrow2000=f'\left(2\right)-2f'\left(4\right)\Rightarrow4000=2f'\left(2\right)-4f'\left(4\right)\) (2)
Cộng vế (1) và (2):
\(f'\left(1\right)-4f'\left(4\right)=4018\)
Đặt \(h\left(x\right)=f\left(x\right)-f\left(4x\right)\Rightarrow h'\left(x\right)=f'\left(x\right)-4f'\left(4x\right)\)
Thay \(x=1\Rightarrow h'\left(1\right)=f'\left(1\right)-4f'\left(4\right)=4018\)
1) Cho hàm số y = f(x) = 2x - 3.
a) Tính f(2); f(0); f(-3); f(![]() )
)
b) Tìm giá trị của x để f(x) = 5
c) Trong hai điểm M(0; -3); N(3; 1), điểm nào thuộc đồ thị hàm số trên?
2)
a) Vẽ hệ trục tọa độ Oxy và đánh dấu các điểm A(2; -2); B(-3;1/2); C(0; 2); D(-3; 0)
3) Vẽ đồ thị của hàm số y = 2x và y = - 1/2x trên cùng một hệ trục tọa độ.
Đạo hàm y 0 = −3x 2 + 6x + m − 1. Hàm số đã cho đồng biến trên khoảng (0; 3) khi và chỉ khi y 0 > 0, ∀x ∈ (0; 3). Hay −3x 2 + 6x + m − 1 > 0, ∀x ∈ (0; 3) ⇔ m > 3x 2 − 6x + 1, ∀x ∈ (0; 3) (∗). Xét hàm số f(x) = 3x 2 − 6x + 1 trên đoạn [0; 3] có f 0 (x) = 6x − 6; f 0 (x) = 0 ⇔ x = 1. Khi đó f(0) = 1, f(3) = 10, f(1) = −2, suy ra max [0;3] f(x) = f(3) = 10. Do đó (∗) ⇔ m > max [0;3] f(x) ⇔ m > 10. Vậy với m > 10 thì hàm số đã cho đồng biến trên khoảng (0; 3).
1/ Cho hàm số \(f\)(\(x\))=\(\dfrac{1}{3}\)\(x\)\(^3\)+\(x \)\(^2\)-(\(m\)+1)\(x\)-\(m\)+3. Với \(m\) là tham số. Có bao nhiêu số nguyên \(m\) thuộc đoạn [-10;10] để \(f\)'(\(x\)) ≥ 0, ∀\(x\) ϵ \(R\)
2/ Cho hàm số \(y\) = \(\dfrac{mx+4}{x+m}\). Với \(m\) là tham số. Có bao nhiêu số nguyên m thuộc đoạn [-5;2023] để \(y\)' > 0, ∀\(x\) ϵ (0;+∞).
1: \(f'\left(x\right)=\dfrac{1}{3}\cdot3x^2+2x-\left(m+1\right)=x^2+2x-m-1\)
\(\Delta=2^2-4\left(-m-1\right)=4m+8\)
Để f'(x)>=0 với mọi x thì 4m+8<=0 và 1>0
=>m<=-2
=>\(m\in\left\{-10;-9;...;-2\right\}\)
=>Có 9 số
Cho hàm số y=f(x) có đạo hàm f'(x)= x ( x - 1 ) 2 ( x 2 + m x + 9 ) . Có bao nhiêu số nguyên dương m để hàm số y=f(3-x) đồng biến trên khoảng ( 3 ; + ∞ ) .
A. 6.
B. 8.
C. 5.
D. 7.
cho hàm số y= f(x)=(m-3)x + m-2 a)tìm m để hàm số trên là hàm số đồng biến b) tìm m biết f(-1)=1
a: Để hàm số đồng biến thì m-3>0
hay m>3
b: Thay x=-1 và y=1 vào (d), ta được:
-m+3+m-2=1
hay 1=1(đúng)
Cho hai hàm số \(f\left( x \right) = {x^3} + x\) và \(g\left( x \right) = {x^2} + 1\,\,\left( {x \in \mathbb{R}} \right).\) Hãy cho biết:
a) Hai hàm số \(f\left( x \right),g\left( x \right)\) có liên tục tại \(x = 2\) hay không.
b) Các hàm số \(f\left( x \right) + g\left( x \right);f\left( x \right) - g\left( x \right);f\left( x \right).g\left( x \right);\frac{{f\left( x \right)}}{{g\left( x \right)}}\) có liên tục tại \(x = 2\) hay không.
a) Ta có \(f\left( x \right),g\left( x \right)\) là các hàm đa thức nên các hàm số \(f\left( x \right),g\left( x \right)\) liên tục trên \(\mathbb{R}\)
Vậy các hàm số \(f\left( x \right),g\left( x \right)\) liên tục tại \(x = 2\)
b) \(\begin{array}{l}f\left( x \right) + g\left( x \right) = {x^3} + {x^2} + x + 1\\f\left( x \right) - g\left( x \right) = {x^3} - {x^2} + x - 1\\f\left( x \right).g\left( x \right) = \left( {{x^3} + x} \right)\left( {{x^2} + 1} \right) = {x^5} + 2{x^3} + x\\\frac{{f\left( x \right)}}{{g\left( x \right)}} = \frac{{{x^3} + x}}{{{x^2} + 1}} = \frac{{x\left( {{x^2} + 1} \right)}}{{{x^2} + 1}} = x\end{array}\)
Ta có \(f\left( x \right) + g\left( x \right);f\left( x \right) - g\left( x \right);f\left( x \right).g\left( x \right);\frac{{f\left( x \right)}}{{g\left( x \right)}}\) là các hàm đa thức nên các hàm số \(f\left( x \right),g\left( x \right)\) liên tục trên \(\mathbb{R}\)
Vậy các hàm số \(f\left( x \right) + g\left( x \right);f\left( x \right) - g\left( x \right);f\left( x \right).g\left( x \right);\frac{{f\left( x \right)}}{{g\left( x \right)}}\) liên tục tại \(x = 2\)
a) Cho hàm số
y = f ( x ) = 2 3 x
Tính: f(-2); f(-1); f(0); f(1/2); f(1); f(2); f(3)
b) Cho hàm số
y = g ( x ) = 2 3 x + 3
Tính: g(-2); g(-1); g(0); g(1/2); g(1); g(2); g(3)
c) Có nhận xét gì về giá trị của hai hàm số đã cho ở trên khi biến x lấy cùng một giá trị?
a) Ta có:
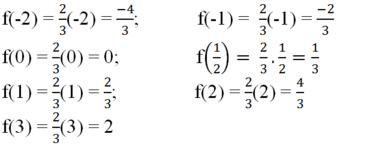
b) Ta có:
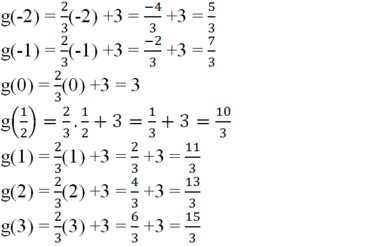
c) Từ kết quả câu a, b ta được bảng sau:

Nhận xét:
- Hai hàm số
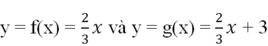
là hai hàm số đồng biến vì khi x tăng thì y cũng nhận được các giá trị tương ứng tăng lên.
- Cùng một giá trị của biến x, giá trị của hàm số y = g(x) luôn luôn lớn hơn giá trị tương ứng của hàm số y = f(x) là 3 đơn vị.
Bài 1. Cho hai hàm số (P): y = f(x) = 3x2 và (d) : y = x + 2
a) Vẽ đồ thị hai hàm số trên cùng một mặt phẳng tọa độ .
b) Tìm tọa độ giao điểm của (P) và (d)
c) Tính f(-1), f(2), f(1/3)
Bài 2:Cho hệ phương trình:
Tìm điều kiện của m để hệ phương trình đã cho có nghiệm duy nhất? Hệ vô nghiệm?
Bài 3. (3 điểm). Cho tam giác ABC nhọn (AB < AC) nội tiếp trong đường tròn (O; R). Gọi H là giao điểm của ba đường cao AD, BE, CF của tam giác ABC.
a) Chứng minh rằng tứ giác BDHF, BFEC nội tiếp đường tròn.
b) Vẽ đường kính AK của đường tròn (O). Cho , tính số đo các góc của tam giác AKC.
Giúp mình với ạ, mình đang cần gấp!!
1:
a: 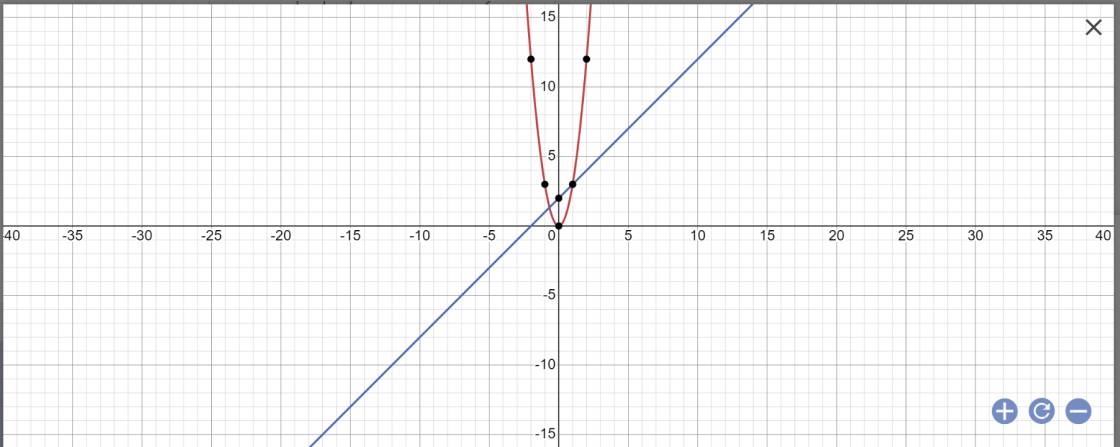
b: PTHĐGĐ là:
3x^2-x-2=0
=>3x^2-3x+2x-2=0
=>(x-1)(3x+2)=0
=>x=1 hoặc x=-2/3
Khi x=1 thì y=3*1^2=3
Khi x=-2/3 thì y=3*4/9=4/3
c: f(-1)=3(-1)^2=3
f(2)=3*2^2=12
f(1/3)=3*(1/3)^2=1/3
Cho hai hàm số f(x)=x+2 và g ( x ) = x 2 - 2 x + 3 Đạo hàm của hàm số y = g f x tại x=1 bằng
A. 4
B. 1
C. 3
D. 2