Giải phương trình sin x 2 + cos x 2 2 + 3 cos x = 2
![]()
![]()
![]()
![]()
giải phương trình sin^2 x − 4√3 sin x · cos x + cos^2 x = −2.
Với \(cosx=0\) ko phải nghiệm
Với \(cosx\ne0\) chia 2 vế cho \(cos^2x\)
\(\Rightarrow tan^2x-4\sqrt{3}tanx+1=-2\left(1+tan^2x\right)\)
\(\Leftrightarrow3tan^2x-4\sqrt{3}tanx+3=0\)
\(\Rightarrow\left[{}\begin{matrix}tanx=\sqrt{3}\\tanx=\dfrac{\sqrt{3}}{3}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k\pi\\x=\dfrac{\pi}{6}+k\pi\end{matrix}\right.\)
Giải phương trình cos x + cos 3 x = sin x - sin 3 x .
A . x = - π 4 + k π 2 k ∈ ℤ
B . x = π 4 + k π 2 k ∈ ℤ
C . x = π 4 + k π k ∈ ℤ
D . x = π 4 + k 2 π k ∈ ℤ
câu này nhìn ngứa mắt quá làm kiểu gì giờ ???
Giải phương trình
\(\sin\dfrac{5x}{2}=5\cos^3x\sin\dfrac{x}{2}\)
Giải các phương trình: sin x + cos x = 1 + sin x . cos x
sin x + cos x = 1 + sin x.cos x
⇔ sin x.cos x – sin x – cos x + 1 = 0
⇔ (sinx. cosx –sinx)- (cosx -1 ) =0
⇔ sinx. (cosx – 1) – (cosx -1) = 0
⇔ (sin x – 1)(cos x – 1) = 0
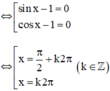
Vậy phương trình có tập nghiệm 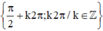
Giải phương trình sau:
a) $\tan ^2x+4\cos ^2x+7=4\tan x+8\cot x$
b) $6\sin ^2x+2\cos ^2x-2\sqrt{3}\sin 2x=14\sin \left(x-\frac{\pi }{6}\right)$
Giải phương trình cos 4 x + 12 sin x . cos x - 5 = 0
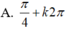
![]()
![]()
Giải phương trình
\(\sin x+2\cos x+2\tan x+4\cot x+6=0\)
Giải các phương trình sau: a) \(2\cos x = - \sqrt 2 \); b) \(\cos 3x - \sin 5x = 0\)
a) \(2\cos x = - \sqrt 2 \Leftrightarrow \cos x = - \frac{{\sqrt 2 }}{2}\;\; \Leftrightarrow \cos x = \cos \frac{\pi }{4} \Leftrightarrow \;\left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{4} + k2\pi }\\{x = \pi - \frac{\pi }{4} + k2\pi }\end{array}} \right.\;\;\;\;\;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{4} + k2\pi }\\{x = \frac{{3\pi }}{4} + k2\pi }\end{array}\;\left( {k \in \mathbb{Z}} \right)} \right.\)
b) \(\cos 3x - \sin 5x = 0\;\;\;\; \Leftrightarrow \cos 3x = \sin 5x\;\;\;\; \Leftrightarrow \cos 3x = \cos \left( {\frac{\pi }{2} - 5x} \right)\;\;\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{3x = \frac{\pi }{2} - 5x + k2\pi }\\{3x = - \frac{\pi }{2} + 5x + k2\pi }\end{array}} \right.\;\;\;\;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{8x = \frac{\pi }{2} + k2\pi }\\{ - 2x = - \frac{\pi }{2} + k2\pi }\end{array}} \right.\;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{{16}} + \frac{{k\pi }}{4}}\\{x = \frac{\pi }{4} - k\pi }\end{array}} \right.\;\;\left( {k \in \mathbb{Z}} \right)\)
Giải các phương trình sau :
a) \(\cos^2x+2\sin x\cos x+5\sin^2x=2\)
b) \(3\cos^2x-2\sin2x+\sin^2x=1\)
c) \(4\cos^2x-3\sin x\cos x+3\sin^2x=1\)
Giải phương trình
\(\left(2\cos x+\sqrt{3}\right)\left(\cos2x+2\sin x-\sqrt{3}\right)=1-4\sin^2x\)
\(\left(2cosx+\sqrt{3}\right)\left(cos2x+2sinx-\sqrt{3}\right)=1-4\left(1-cos^2x\right)\)
\(\Leftrightarrow\left(2cosx+\sqrt{3}\right)\left(cos2x+2sinx-\sqrt{3}\right)=4cos^2x-3\)
\(\Leftrightarrow\left(2cosx+\sqrt{3}\right)\left(cos2x+2sinx-\sqrt{3}\right)=\left(2cosx+\sqrt{3}\right)\left(2cosx-\sqrt{3}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=-\dfrac{\sqrt{3}}{2}\Rightarrow x=...\\cos2x+2sinx-\sqrt{3}=2cosx-\sqrt{3}\left(1\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow cos^2x-sin^2x-2\left(cosx-sinx\right)=0\)
\(\Leftrightarrow\left(cosx-sinx\right)\left(cosx+sinx\right)-2\left(cosx-sinx\right)=0\)
\(\Leftrightarrow\left(cosx-sinx\right)\left(cosx+sinx-2\right)=0\)
\(\Leftrightarrow...\)