Hàm số y = 2.cos 3x + 3.sin 3x - 2 có tất cả bao nhiêu giá trị nguyên
A. 7
B. 3
C. 5
D. 6
Những câu hỏi liên quan
Nguyên hàm sin ( bi chia 4 — x )dx
Nguyên hàm ( 7/cos^2(3—x) + 8 sin(9—3x) — 1/x + 6/3—2x + căn x )dx
Nguyên hàm (7/cos^2x — 8/ 2x+1 +9^2x+1 + e^5—2x +8) dx
Nguyên hàm ( 3—căn x + 5x^5—6x^7+1 tất cả / x )dx
Xem chi tiết
Tính tổng tất cả các giá trị nguyên của hàm số
y
3
.
sin
x
-
cos
x
-
4
2...
Đọc tiếp
Tính tổng tất cả các giá trị nguyên của hàm số y = 3 . sin x - cos x - 4 2 . sin x + cos x - 3
A. 8
B. 5
C. 6
D. 9
23 tháng 8 2021 lúc 20:48
câu 1 Có bao nhiêu giá trị nguyên của x thỏa mãn cả hai bất phương trình sau:
\(\dfrac{x+2}{5}-\dfrac{3x-7}{4}>-5\)
và \(\dfrac{3x}{5}-\dfrac{x-4}{3}+\dfrac{x+2}{6}>6\)
a, 3 b,1 c,4 d,2
Cho hàm số
f
x
m
-
1
x
3
-
5
x
2
+
m
+
3
x
+
3
. Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số
y
f...
Đọc tiếp
Cho hàm số f x = m - 1 x 3 - 5 x 2 + m + 3 x + 3 . Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số y = f x có đúng 3 điểm cực trị ?
A. 1.
B. 4.
C. 5.
D. 3.
TXĐ: D = R .
TH1: m = 1 . Khi đó hàm số trở thành:
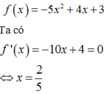
BBT:
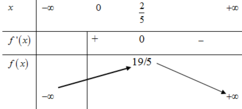
Từ đó ta suy ra BBT của hàm số y = f x như sau:
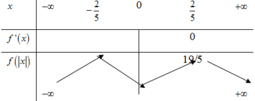
Hàm số có 3 điểm cực trị, do đó m = 1 thỏa mãn.
TH2: m ≠ 1 Để hàm số y = f x có 3 điểm cực trị thì hàm số y = f x có 2 điểm cực trị trái dấu.
Ta có:
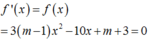
Để hàm số có 2 cực trị trái dấu ⇔ f x = 0 có 2 nghiệm trái dấu
Chọn B.
Đúng 0
Bình luận (0)
Cho hàm số
f
(
x
)
m
-
1
x
3
-
5
x
2
+
m
+
3
x
+
3
. Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số
y
...
Đọc tiếp
Cho hàm số f ( x ) = m - 1 x 3 - 5 x 2 + m + 3 x + 3 . Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số y = f x có đúng 3 điểm cực trị?
A. 1.
B. 5.
C. 3.
D. 4.
Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số y=|3x⁴-mx³+6x²+m-3| đồng biến trên khoảng (0- dương vô cùng)
SGK Kết nối tri thức và cuộc sống
17 tháng 8 2023 lúc 10:44
Tính đạo hàm của các hàm số sau:
a) \(y = x{\sin ^2}x;\)
b) \(y = {\cos ^2}x + \sin 2x;\)
c) \(y = \sin 3x - 3\sin x;\)
d) \(y = \tan x + \cot x.\)
tham khảo:
a)\(y'=xsin2x+sin^2x\)
\(y'=sin^2x+xsin2x\)
b)\(y'=-2sin2x+2cosx\\ y'=2\left(cosx-sin2x\right)\)
c)\(y=sin3x-3sinx\)
\(y'=3cos3x-3cosx\)
d)\(y'=\dfrac{1}{cos^2x}-\dfrac{1}{sin^2x}\)
\(y'=\dfrac{sin^2x-cos^2x}{sin^2x.cos^2x}\)
Đúng 1
Bình luận (0)
Trong các hàm số dưới đây có bao nhiêu hàm số là hàm số chẵn: y cos 3x (1); y sin (x2 + 1) (2) ; y tan2 x (3); y cot x (4); A. 1 . B. 2 C. 3 . D. 4
Đọc tiếp
Trong các hàm số dưới đây có bao nhiêu hàm số là hàm số chẵn:
y = cos 3x (1); y = sin (x2 + 1) (2) ;
y = tan2 x (3); y = cot x (4);
A. 1 .
B. 2
C. 3 .
D. 4
Đáp án C.
+ Xét hàm y = f(x) = cos 3x
TXĐ: D = R
Với mọi x ∈ D, ta có: -x ∈ D và f(-x) = cos (-3x) = cos 3x = f(x)
Do đó, y = f(x) = cos 3x là hàm chẵn trên tập xác định của nó.
+ Xét hàm y = g(x) = sin (x2 + 1)
TXĐ: D = R
Với mọi x ∈ D, ta có: -x ∈ D và g(-x) = sin ((-x)2 + 1) = sin (x2 + 1) = g(x)
Do đó: y = g(x) = sin (x2 + 1) là hàm chẵn trên R.
+ Xét hàm y = h(x) = tan2 x
TXĐ: D = R\{π/2 + k2π, k ∈ Z)
Với mọi x ∈ D, ta có: -x ∈ D và h(-x) = tan2 (-x) = tan2 x = h(x)
Do đó: y = h(x) = tan2 x là hàm số chẵn trên D
+ Xét hàm y = t(x) = cot x.
TXĐ: D = R\{kπ, k ∈ Z)
Với mọi x ∈ D, ta có: -x ∈ D và t(-x) = cot (-x) = -cot x = -t(x)
Do đó: y = t(x) = cot x là hàm số lẻ trên D.
Đúng 0
Bình luận (0)
Tìm đạo hàm các hàm số:
1, \(y=\tan(3x-\dfrac{\pi}{4})+\cot(2x-\dfrac{\pi}{3})+\cos(x+\dfrac{\pi}{6})\)
2, \(y=\dfrac{\sqrt{\sin x+2}}{2x+1}\)
3, \(y=\cos(3x+\dfrac{\pi}{3})-\sin(2x+\dfrac{\pi}{6})+\cot(x+\dfrac{\pi}{4})\)
a.
\(y'=\dfrac{3}{cos^2\left(3x-\dfrac{\pi}{4}\right)}-\dfrac{2}{sin^2\left(2x-\dfrac{\pi}{3}\right)}-sin\left(x+\dfrac{\pi}{6}\right)\)
b.
\(y'=\dfrac{\dfrac{\left(2x+1\right)cosx}{2\sqrt{sinx+2}}-2\sqrt{sinx+2}}{\left(2x+1\right)^2}=\dfrac{\left(2x+1\right)cosx-4\left(sinx+2\right)}{\left(2x+1\right)^2}\)
c.
\(y'=-3sin\left(3x+\dfrac{\pi}{3}\right)-2cos\left(2x+\dfrac{\pi}{6}\right)-\dfrac{1}{sin^2\left(x+\dfrac{\pi}{4}\right)}\)
Đúng 2
Bình luận (0)