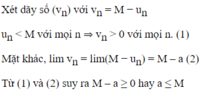Cho hai dãy số ( u n ) và ( v n ) . Chứng minh rằng nếu lim v n = 0 v à | u n | ≥ v n với mọi n thì l i m u n = 0

Những câu hỏi liên quan
Cho dãy số ( u n ) thoả mãn u n > M với mọi n. Chứng minh rằng nếu l i m u n = a thì a ≤ M
Cho hai dãy số \(\left(u_n\right)\) và \(\left(v_n\right)\). Chứng minh rằng nếu \(\lim\limits v_n=0\) và \(\left|u_n\right|\le v_n\) với mọi n thì \(\lim\limits u_n=0\) ?
Biết dãy số
u
n
thỏa mãn
u
n
-
1
1
3
với mọi n. Chứng minh rằng:
l
i
m
u
n
...
Đọc tiếp
Biết dãy số u n thỏa mãn u n - 1 < 1 3 với mọi n. Chứng minh rằng: l i m u n = 1 .
Đặt vn = un – 1.
Lấy số dương d > 0 bé tùy ý
⇒ luôn tồn tại 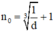 thỏa mãn
thỏa mãn 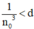
⇒ 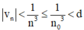 với mọi n ≥ n0.
với mọi n ≥ n0.
⇒ Theo định nghĩa ta có:
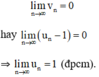
Đúng 0
Bình luận (0)
Cho dãy số xác định bởi u1=1/2 un+1=un^2+1/2
a,chứng minh rằng un<1mọi n
b,chứng minh ưn trang và bị chặn trên
c,Tính lim un
Bài này sai đề rồi
\(u_1=\frac{1}{2}< 1\)
\(u_2=u_1^2+1=\left(\frac{1}{2}\right)^2+\frac{1}{2}=\frac{3}{4}< 1\)
\(u_3=u_2^2+1=\left(\frac{3}{4}\right)^2+\frac{1}{2}=\frac{9}{16}+\frac{8}{16}=\frac{17}{16}>1\)
cho dãy số 1,3,6,10,15,...,n(n+1)/2,... chứng minh rằng tổng hai số hạng liên tiếp của dãy bao giờ cũng là số chính phương
Hai số hạng liên tiếp của dãy có dạng:
\(\dfrac{\left(n-1\right)n}{2}\) và \(\dfrac{n\left(n+1\right)}{2}\) với \(n\ge2\)
Tổng của 2 số hạng liên tiếp:
\(\dfrac{\left(n-1\right)n}{2}+\dfrac{n\left(n+1\right)}{2}=\dfrac{n}{2}\left(n-1+n+1\right)=n^2\) là 1 SCP (đpcm)
Đúng 1
Bình luận (0)
B.1.Chứng minh rằng:
A. 22010 +2 2013 là số chính phương
B. Với n là số tự nhiên lớn hơn 0 thì hai số n2 +n và 2n+1 là hai số nguyên tố cùng nhau
C. Nếu số abc chia hết cho 27 thì số bác cũng chia hết cho 27
2, Tìm số tự nhiên A biết rằng 442 chia A dư 22 và 321 chia A dư 21
3,
A. Chứng tỏ
108 + 8 chia hết cho 72
B. Cho A và B là các số tự nhiên chứng minh rằng : Nếu a +2b thì 3a -10b chia hết cho 8 và ngược lại
Đọc tiếp
B.1.Chứng minh rằng:
A. 22010 +2 2013 là số chính phương
B. Với n là số tự nhiên lớn hơn 0 thì hai số n2 +n và 2n+1 là hai số nguyên tố cùng nhau
C. Nếu số abc chia hết cho 27 thì số bác cũng chia hết cho 27
2, Tìm số tự nhiên A biết rằng 442 chia A dư 22 và 321 chia A dư 21
3,
A. Chứng tỏ
108 + 8 chia hết cho 72
B. Cho A và B là các số tự nhiên chứng minh rằng : Nếu a +2b thì 3a -10b chia hết cho 8 và ngược lại
Cho một dãy số nguyên A gồm N phần tử A1, A2,…, AN và hai số nguyên dương U, V (1 ≤ U ≤ V ≤ N). Hãy tìm một đoạn con liên tiếp của dãy A có tổng các phần tử đạt giá trị lớn nhất và độ dài là D tùy ý với U ≤ D ≤ V. (Độ dài của đoạn con là số lượng phần tử trên đoạn con đó).input out5 12 3 -4 3 -2 -6 5giúp em với c++ ạ
Đọc tiếp
Cho một dãy số nguyên A gồm N phần tử A1, A2,…, AN và hai số nguyên dương U, V (1 ≤ U ≤ V ≤ N). Hãy tìm một đoạn con liên tiếp của dãy A có tổng các phần tử đạt giá trị lớn nhất và độ dài là D tùy ý với U ≤ D ≤ V. (Độ dài của đoạn con là số lượng phần tử trên đoạn con đó).
input out
5 1
2 3 -4 3 -2 -6 5
giúp em với c++ ạ
Cho hai dãy số
(
u
n
)
và
(
v
n
)
. Biết
l
i
m
u
n
−
∞
và
v
n
≤
u
n
với mọi n. Có kết luận gì về giới hạn của dãy
(
v
n...
Đọc tiếp
Cho hai dãy số ( u n ) và ( v n ) . Biết l i m u n = − ∞ và v n ≤ u n với mọi n. Có kết luận gì về giới hạn của dãy ( v n ) khi n → + ∞ ?
Vì l i m u n = − ∞ nên l i m ( − u n ) = + ∞ . Do đó ( − u n ) có thể lớn hơn một số dương lớn tuỳ ý, kể từ một số hạng nào đó trở đi. (1)
Mặt khác, vì v n ≤ u n với mọi n nên ( − v n ) ≥ ( − u n ) với mọi n. (2)
Từ (1) và (2) suy ra ( − v n ) có thể lớn hơn một số dương lớn tuỳ ý, kể từ một số hạng nào đó trở đi. Do đó, l i m ( − v n ) = + ∞ hay l i m v n = − ∞
Đúng 0
Bình luận (0)
Cho dãy số \(\left(u_n\right)\) thỏa mãn \(u_n< M\) với mọi \(n\). Chứng minh rằng nếu \(\lim\limits u_n=a\) thì \(a\le M\) ?