Hai đường thẳng ( d 1 ) và ( d 2 ) cắt nhau tại M(2; -5) nên:

M ∈ ( d 1  ): 3 a - 1 2 + 2b.(-5) = 56 ⇔ 6a - 10b = 58

Khi đó, ta có hệ phương trình:

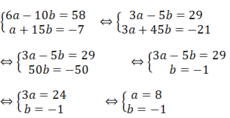
Vậy a = 8 và b = -1 thì hai đường thẳng ( d 1  ) và ( d 2  ) cắt nhau tại M(2; -5).

Theo đề, ta có:

\(\left\{{}\begin{matrix}2\left(3a-1\right)-10b=56\\\dfrac{1}{2}\cdot a\cdot2+5\left(3b-2\right)=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}6a-10b=58\\a+15b=13\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}6a-10b=58\\6a+90b=78\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=\dfrac{1}{5}\\a=10\end{matrix}\right.\)

a: Theo đề, ta có:

\(\left\{{}\begin{matrix}a+b=5\\2a+b=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=3\\b=2\end{matrix}\right.\)

b: 

1: Thay x=-1 và y=3 vào (d), ta được:

\(2\cdot\left(-1\right)-a+1=3\)

=>-a-1=3

=>-a=4

hay a=-4

tra góc le đi

a: Thay m=2 vào y=(m-1)x+m-1, ta được:

y=(2-1)x+2-1=x+1

Phương trình hoành độ giao điểm là:

x+1=-x+1

=>2x=0

=>x=0

Thay x=0 vào y=x+1, ta được:

y=0+1=1

Vậy: Tọa độ giao điểm là A(0;1)

b: Thay x=3 và y=4 vào y=(m-1)x+m-1, ta được;

3(m-1)+m-1=4

=>4(m-1)=4

=>m-1=1

=>m=2

c: Để hai đường thẳng này cắt nhau thì \(m-1\ne-1\)

=>\(m\ne0\)

a) √(√3 - 2)² + √3

= 2 - √3 + √3

= 2

b) Để (d) và (d') cắt nhau thì:

m + 2 ≠ -2

m ≠ -2 - 2

m ≠ -4

Vậy m ≠ -4 thì (d) cắt (d')

c) Thay tọa độ điểm A(3; -1) vào (d) ta có:

(2m - 3).3 + m = -1

⇔ 6m - 9 + m = -1

⇔ 7m = -1 + 9

⇔ 7m = 8

⇔ m = 8/7 (nhận)

Thay m = 8/7 vào (d) ta có:

(d): y = -5x/7 - 8/7

Vậy hệ số góc của (d) là -5/7

a: Thay x=2 và y=-3 vào (d), ta được:

\(2\left(2m-1\right)-2m+5=-3\)

=>\(4m-2-2m+5=-3\)

=>2m+3=-3

=>2m=-6

=>\(m=-\dfrac{6}{2}=-3\)

b: Để (d)//(d') thì \(\left\{{}\begin{matrix}2m-1=2\\-2m+5\ne1\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}2m=3\\-2m\ne-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{3}{2}\\m\ne2\end{matrix}\right.\)

=>m=3/2

Thay m=3/2 vào (d), ta được:

\(y=\left(2\cdot\dfrac{3}{2}-1\right)x-2\cdot\dfrac{3}{2}+5=2x+2\)

y=2x+2 nên a=2

Gọi \(\alpha\) là góc tạo bởi (d) với trục Ox

\(tan\alpha=2\)

=>\(\alpha\simeq63^026'\)

Bài 3 làm sao v ạ?