Nếu sinx + cosx= 1/2 thì 3sinx + 2cosx bằng
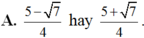
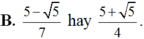
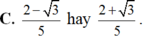
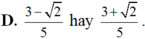
Nếu sinx + cosx = 1/2 thì 3sinx + 2cosx bằng
![]()
![]()
![]()
![]()
Chọn A.
Ta có:
sinx + cosx = ½ nên ( sinx + cosx)2 = ¼
Do đó sinx. cosx = -3/8
Khi đó sinx; cosx là nghiệm của phương trình
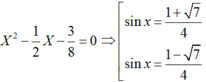
Ta có sinx + cos x = ½ nên 2( sinx + cosx) = 1
+) Với 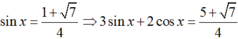
+) Với 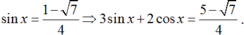
(2sinx+cosx)(sinx+cosx) =3sinx +2cosx
Giải pt
\(2sin\left(x+\dfrac{\pi}{6}\right)+sinx+2cosx=3\)
\(\left(sin2x+cos2x\right)cosx+2cos2x-sinx=0\)
\(sin2x-cos2x+3sinx-cosx-1=0\)
1.
\(2sin\left(x+\dfrac{\pi}{6}\right)+sinx+2cosx=3\)
\(\Leftrightarrow\sqrt{3}sinx+cosx+sinx+2cosx=3\)
\(\Leftrightarrow\left(\sqrt{3}+1\right)sinx+3cosx=3\)
\(\Leftrightarrow\sqrt{13+2\sqrt{3}}\left[\dfrac{\sqrt{3}+1}{\sqrt{13+2\sqrt{3}}}sinx+\dfrac{3}{\sqrt{13+2\sqrt{3}}}cosx\right]=3\)
Đặt \(\alpha=arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}\)
\(pt\Leftrightarrow\sqrt{13+2\sqrt{3}}sin\left(x+\alpha\right)=3\)
\(\Leftrightarrow sin\left(x+\alpha\right)=\dfrac{3}{\sqrt{13+2\sqrt{3}}}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\alpha=arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}+k2\pi\\x+\alpha=\pi-arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=\pi-2arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}+k2\pi\end{matrix}\right.\)
Vậy phương trình đã cho có nghiệm:
\(x=k2\pi;x=\pi-2arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}+k2\pi\)
2.
\(\left(sin2x+cos2x\right)cosx+2cos2x-sinx=0\)
\(\Leftrightarrow2sinx.cos^2x+cos2x.cosx+2cos2x-sinx=0\)
\(\Leftrightarrow\left(2cos^2x-1\right)sinx+cos2x.cosx+2cos2x=0\)
\(\Leftrightarrow cos2x.sinx+cos2x.cosx+2cos2x=0\)
\(\Leftrightarrow cos2x.\left(sinx+cosx+2\right)=0\)
\(\Leftrightarrow cos2x=0\)
\(\Leftrightarrow2x=\dfrac{\pi}{2}+k\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)
Vậy phương trình đã cho có nghiệm \(x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)
giải pt : \(\dfrac{2cos2x+1}{\sqrt{3}sinx+cosx}\)=2cosx-1
tìm txđ hàm số D: y=\(\dfrac{2+3sinx}{2sin2x+\sqrt{2}}\)
Giải các phương trình sau:
a, \(\sqrt{2}\) sin \(\left(2x+\frac{\pi}{4}\right)\)=3sinx+cosx+2
b, 1+sinx+cosx+sin2x+cos2x=0
c, (2cosx-1)(2sinx+cosx)=sin2x-sinx
d, cos3x+cos2x-cosx-1=0
a.
\(\Leftrightarrow sin2x+cos2x=3sinx+cosx+2\)
\(\Leftrightarrow2sinx.cosx-3sinx+2cos^2x-cosx-3=0=0\)
\(\Leftrightarrow sinx\left(2cosx-3\right)+\left(cosx+1\right)\left(2cosx-3\right)=0\)
\(\Leftrightarrow\left(sinx+cosx+1\right)\left(2cosx-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx+cosx=-1\\2cosx-3=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}sin\left(x+\frac{\pi}{4}\right)=-\frac{\sqrt{2}}{2}\\cosx=\frac{3}{2}\left(vn\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\frac{\pi}{4}=-\frac{\pi}{4}+k2\pi\\x+\frac{\pi}{4}=\frac{5\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow...\)
b.
\(\Leftrightarrow1+sinx+cosx+2sinx.cosx+2cos^2x-1=0\)
\(\Leftrightarrow sinx\left(2cosx+1\right)+cosx\left(2cosx+1\right)=0\)
\(\Leftrightarrow\left(sinx+cosx\right)\left(2cosx+1\right)=0\)
\(\Leftrightarrow\sqrt{2}sin\left(x+\frac{\pi}{4}\right)\left(2cosx+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin\left(x+\frac{\pi}{4}\right)=0\\cosx=-\frac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\frac{\pi}{4}+k\pi\\x=\frac{2\pi}{3}+k2\pi\\x=-\frac{2\pi}{3}+k2\pi\end{matrix}\right.\)
c.
\(\Leftrightarrow\left(2cosx-1\right)\left(2sinx+cosx\right)=2sinx.cosx-sinx\)
\(\Leftrightarrow\left(2cosx-1\right)\left(2sinx+cosx\right)-sinx\left(2cosx-1\right)=0\)
\(\Leftrightarrow\left(2cosx-1\right)\left(2sinx+cosx-sinx\right)=0\)
\(\Leftrightarrow\left(2cosx-1\right)\left(sinx+cosx\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2cosx-1=0\\sinx+cosx=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=\frac{1}{2}\\sin\left(x+\frac{\pi}{4}\right)=0\end{matrix}\right.\)
\(\Leftrightarrow...\)
mọi người giải chi tiết dùm e 3 bài này với
a) \(2cosx-3sinx+2=0\)
b) \(\dfrac{1+sinx}{1+cosx}=\dfrac{1}{2}\)
c) \(cos\left(2x-15^0\right)+sin\left(2x-15^0\right)=-1\)
a ) \(2cosx-3sinx+2=0\)
\(\Leftrightarrow2cosx-3sinx=-2\)
\(\Leftrightarrow\dfrac{2}{\sqrt{13}}cosx-\dfrac{3}{\sqrt{13}}sinx=-\dfrac{2}{\sqrt{13}}\)
Thấy : \(\left(\dfrac{2}{\sqrt{13}}\right)^2+\left(\dfrac{-3}{\sqrt{13}}\right)^2=1\) nên tồn tại \(\alpha\) t/m :
\(sin\alpha=\dfrac{2}{\sqrt{13}};cos\alpha=\dfrac{-3}{\sqrt{13}}\) . . Khi đó : \(sin\alpha.cosx+cos\alpha.sinx=\dfrac{-2}{\sqrt{13}}\)
\(\Leftrightarrow sin\left(\alpha+x\right)=\dfrac{-2}{\sqrt{13}}\) ( p/t cơ bản )
b ) \(\dfrac{1+sinx}{1+cosx}=\dfrac{1}{2}\) ( ĐK : \(cosx\ne-1\Leftrightarrow x\ne\left(2k+1\right)\pi\) ; ( k thuộc Z ) )
\(\Leftrightarrow2+2sinx=cosx+1\) \(\Leftrightarrow cosx-2sinx=1\)
Làm giống như a )
c ) \(cos\left(2x-15^o\right)+sin\left(2x-15^o\right)=-1\)
Đặt \(t=2x-15^o\) ; ta có : \(cos t + sin t = -1\)
\(\Leftrightarrow\sqrt{2}sin\left(t+\dfrac{\pi}{4}\right)=-1\) \(\Leftrightarrow sin\left(t+\dfrac{\pi}{4}\right)=sin\left(-\dfrac{\pi}{4}\right)\)
Xong rồi bn làm tiếp ; chú ý đổi ra độ
giải các pt
a) \(1-2cos2x-\sqrt{3}sinx+cosx=0\)
b) \(cos2x+cos^2x-sinx.cosx=8\left(cosx-sinx\right)\)
c) \(sin^2x+3sinx.cosx-4cos^2x=4\left(sinx-cosx\right)\)
d) \(\frac{cos^3x-sin^3x}{2cosx+3sinx}=cos2x\)
a/
\(\Leftrightarrow1-2\left(2cos^2x-1\right)-\sqrt{3}sinx+cosx=0\)
\(\Leftrightarrow3-4cos^2x+cosx-\sqrt{3}sinx=0\)
\(\Leftrightarrow\left(1-cosx\right)\left(4cosx+3\right)-\sqrt{3}sinx=0\)
\(\Leftrightarrow2sin^2\frac{x}{2}\left(4cosx+3\right)-2\sqrt{3}sin\frac{x}{2}cos\frac{x}{2}=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}sin\frac{x}{2}=0\Rightarrow x=k2\pi\\sin\frac{x}{2}\left(4cosx+3\right)-\sqrt{3}cos\frac{x}{2}=0\left(1\right)\end{matrix}\right.\)
Xét (1) \(\Leftrightarrow sin\frac{x}{2}\left(8cos^2\frac{x}{2}-1\right)-\sqrt{3}cos\frac{x}{2}=0\)
- Với \(\left\{{}\begin{matrix}cos\frac{x}{2}=0\\sin\frac{x}{2}=-1\end{matrix}\right.\) \(\Rightarrow x=-\pi+k4\pi\) là 1 nghiệm
- Với \(cos\frac{x}{2}\ne0\) chia 2 vế cho \(cos^3\frac{x}{2}\)
\(tan\frac{x}{2}\left(8-1-tan^2\frac{x}{2}\right)-\sqrt{3}-\sqrt{3}tan^2\frac{x}{2}=0\)
\(\Leftrightarrow-tan^3\frac{x}{2}-\sqrt{3}tan^2\frac{x}{2}+7tan\frac{x}{2}-\sqrt{3}=0\)
Đặt \(tan\frac{x}{2}=t\)
\(\Rightarrow t^3+\sqrt{3}t^2-7t+\sqrt{3}=0\)
\(\Leftrightarrow\left[{}\begin{matrix}t=\sqrt{3}\\t=-2-\sqrt{3}\\t=2-\sqrt{3}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\frac{x}{2}=\frac{\pi}{3}+k\pi\\\frac{x}{2}=-\frac{5\pi}{12}+k\pi\\\frac{x}{2}=\frac{\pi}{12}+k\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\frac{2\pi}{3}+k2\pi\\x=-\frac{5\pi}{6}+k2\pi\\x=\frac{\pi}{6}+k2\pi\end{matrix}\right.\)
b/
\(\Leftrightarrow cos^2x-sin^2x+cos^2x-sinx.cosx=8\left(cosx-sinx\right)\)
\(\Leftrightarrow\left(cosx-sinx\right)\left(cosx+sinx\right)+cosx\left(cosx-sinx\right)=8\left(cosx-sinx\right)\)
\(\Leftrightarrow\left(cosx-sinx\right)\left(2cosx+sinx-8\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx-sinx=0\left(1\right)\\2cosx+sinx=8\left(2\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow sin\left(x-\frac{\pi}{4}\right)=0\Leftrightarrow x-\frac{\pi}{4}=k\pi\)
\(\Rightarrow x=\frac{\pi}{4}+k\pi\)
Xét (2), theo điều kiện có nghiệm của pt lượng giác bậc nhất, \(2^2+1^2< 8^2\Rightarrow\left(2\right)\) vô nghiệm
c/
\(\Leftrightarrow\left(sinx-cosx\right)\left(sinx+4cosx\right)=4\left(sinx-cosx\right)\)
\(\Leftrightarrow\left(sinx-cosx\right)\left(sinx+4cosx-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx-cosx=0\left(1\right)\\sinx+4cosx-4=0\left(2\right)\end{matrix}\right.\)
Xét (1) \(\Leftrightarrow sin\left(x-\frac{\pi}{4}\right)=0\Leftrightarrow x=\frac{\pi}{4}+k\pi\)
Xét (2) \(\Leftrightarrow\frac{1}{\sqrt{17}}sinx+\frac{4}{\sqrt{17}}cosx=\frac{4}{\sqrt{17}}\)
Đặt \(\frac{4}{\sqrt{17}}=cosa\) với \(a\in\left(0;\pi\right)\)
\(\Rightarrow cosx.cosa+sinx.sina=cosa\)
\(\Leftrightarrow cos\left(x-a\right)=cosa\)
\(\Leftrightarrow\left[{}\begin{matrix}x-a=a+k2\pi\\x-a=-a+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2a+k2\pi\\x=k2\pi\end{matrix}\right.\)
III. Phương trình bậc nhất đối với sinx và cosx:
*Giải các phương trình bậc nhất đối với sinx và cosx sau đây:
(2.1)
1) \(2sinx-2cosx=\sqrt{2}\)
2) \(cosx-\sqrt{3}sinx=1\)
3) \(\sqrt{3}sin\dfrac{x}{3}+cos\dfrac{x}{2}=\sqrt{2}\)
4) \(cosx-sinx=1\)
5) \(2cosx+2sinx=\sqrt{6}\)
6) \(sin3x+\sqrt{3}cosx=\sqrt{2}\)
7) \(3sinx-2cosx=2\)
(2.3)
1) \(\left(sinx-1\right)\left(1+cosx\right)=cos^2x\)
2) \(sin\left(\dfrac{\pi}{2}+2x\right)+\sqrt{3}sin\left(\pi-2x\right)=1\)
3) \(\sqrt{2}\left(cos^4x-sin^4x\right)=cosx+sinx\)
4) \(sin2x+cos2x=\sqrt{2}sin3x\)
5) \(sinx=\sqrt{2}sin5x-cosx\)
6) \(sin8x-cos6x=\sqrt{3}\left(sin6x+cos8x\right)\)
7) \(cos3x-sinx=\sqrt{3}\left(cosx-sin3x\right)\)
8) \(2sin^2x+\sqrt{3}sin2x=3\)
9) \(sin^4x+cos^4\left(x+\dfrac{\pi}{4}\right)=\dfrac{1}{4}\)
(2.3)
1) \(\dfrac{\sqrt{3}\left(1-cos2x\right)}{2sinx}=cosx\)
2) \(cotx-tanx=\dfrac{cosx-sinx}{sinx.cosx}\)
3) \(\dfrac{\sqrt{3}}{cosx}+\dfrac{1}{sinx}=4\)
4) \(\dfrac{1+sinx}{1+cosx}=\dfrac{1}{2}\)
5) \(3cosx+4sinx+\dfrac{6}{3cosx+4sinx+1}=6\)
(2.4)
a) Tìm nghiệm \(x\in\left(\dfrac{2\pi}{5};\dfrac{6\pi}{7}\right)\) của phương trình \(cos7x-\sqrt{3}sin7x+\sqrt{2}=0\)
b) Tìm nghiệm \(x\in\left(0;\pi\right)\) của phương trình \(4sin^2\dfrac{x}{2}-\sqrt{3}cos2x=1+2cos^2\left(x-\dfrac{3\pi}{4}\right)\)
(2.5) Xác định tham số m để các phương trình sau đây có nghiệm:
a) \(mcosx-\left(m+1\right)sinx=m\)
b) \(\left(2m-1\right)sinx+\left(m-1\right)cosx=m-3\)
(2.6) Tìm GTLN, GTNN (nếu có) của các hàm số sau đây:
a) \(y=3sinx-4cosx+5\)
b) \(y=cos2x+sin2x-1\)
2.1
a.
\(\Leftrightarrow sinx-cosx=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\sqrt{2}sin\left(x-\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow sin\left(x-\dfrac{\pi}{4}\right)=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{4}=\dfrac{\pi}{6}+k2\pi\\x-\dfrac{\pi}{4}=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5\pi}{12}+k2\pi\\x=\dfrac{13\pi}{12}+k2\pi\end{matrix}\right.\)
b.
\(cosx-\sqrt{3}sinx=1\)
\(\Leftrightarrow\dfrac{1}{2}cosx-\dfrac{\sqrt{3}}{2}sinx=\dfrac{1}{2}\)
\(\Leftrightarrow cos\left(x+\dfrac{\pi}{3}\right)=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{3}=\dfrac{\pi}{3}+k2\pi\\x+\dfrac{\pi}{3}=-\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=-\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)
c.
\(\sqrt{3}sin\dfrac{x}{3}+cos\dfrac{x}{2}=\sqrt{2}\)
Câu này đề đúng không nhỉ? Nhìn thấy có vẻ không đúng lắm
d.
\(cosx-sinx=1\)
\(\Leftrightarrow\sqrt{2}cos\left(x+\dfrac{\pi}{4}\right)=1\)
\(\Leftrightarrow cos\left(x+\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{4}=\dfrac{\pi}{4}+k2\pi\\x+\dfrac{\pi}{4}=-\dfrac{\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=-\dfrac{\pi}{2}+k2\pi\end{matrix}\right.\)
\(\dfrac{1}{cosx\left(sinx-cosx\right)}=2\sqrt{2}sinx+\dfrac{2cosx}{sinx-cosx}\)
Bài này giải như nào ạ ??? Em cảm ơn trước nha.
Đk: \(\left\{{}\begin{matrix}x\ne\dfrac{\pi}{2}+m2\pi\\x\ne\dfrac{\pi}{4}+n\pi\end{matrix}\right.\left(m,n\in Z\right)\)
PT \(\Leftrightarrow1=2\sqrt{2}sinx.cosx\left(sinx-cosx\right)+2cos^2x\)
\(\Leftrightarrow\sqrt{2}.2sinx.cosx\left(sinx-cosx\right)+\left(2cos^2x-1\right)=0\)
\(\Leftrightarrow\sqrt{2}sin2x\left(sinx-cosx\right)+\left(cosx-sinx\right)\left(cosx+sinx\right)=0\)
\(\Leftrightarrow\sqrt{2}sin2x=sinx+cosx\)
\(\Leftrightarrow\sqrt{2}sin2x=\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=x+\dfrac{\pi}{4}+k2\pi\\2x=\pi-x-\dfrac{\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k2\pi\\x=\dfrac{\pi}{4}+k\dfrac{2\pi}{3}\end{matrix}\right.\left(k\in Z\right)\)