Trong mặt phẳng Oxy cho parabol (P) có phương trình: y = 6 x 2 - 3 x + 13 . Phép đối xứng trục Ox biến (P) thành (P’) có phương trình:
A. y = 6 x 2 + 3 x - 13
B. y = 6 x 2 - 3 x - 13
C. y = - 6 x 2 + 3 x - 13
D. y = - 6 x 2 - 3 x - 13
Trong mặt phẳng toạ độ Oxy, cho parabol (P) y=x^2 và đường thẳng (d) y=x+2.
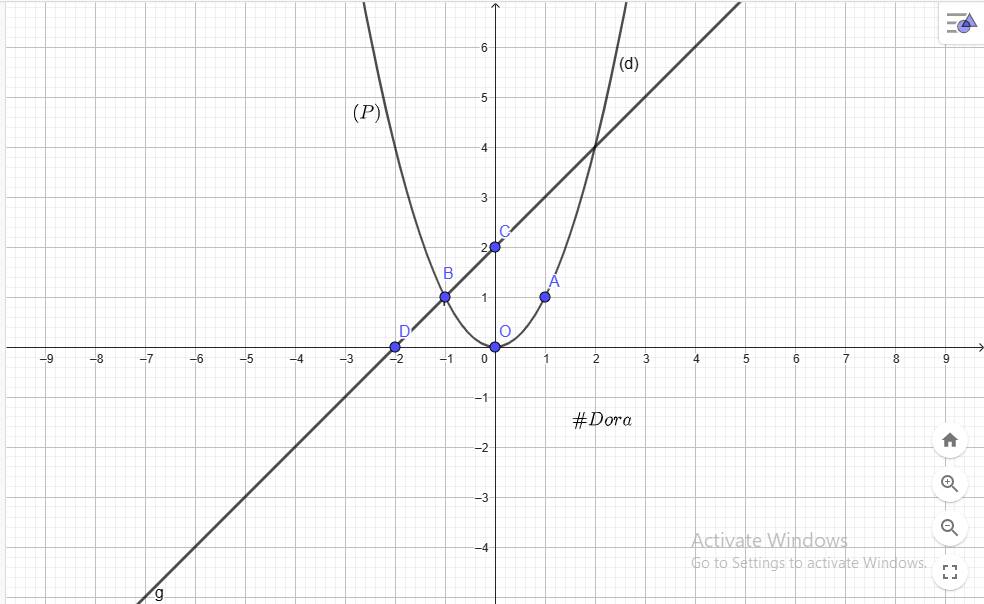
a) vẽ parabol (P) và đường thẳng (d) trên cùng mặt phẳng toạ độ Oxy.
b) Tìm toạ độ giao điểm của (P) và (d) bằng phép tính.
c) viết phương trình đường thẳng (d') có dạng y=ax+b , biết (d') song song với (d) và đi qua điểm M(2:5)
`a)`
`@ O(0;0), A(1;1), B(-1;1) in (P)`
`@ C(0;2), D(-2;0) in (d)`
`b)` Ptr hoành độ của `(P)` và `(d)` là:
`x^2=x+2`
`<=>x^2-x-2=0`
Ptr có: `a-b+c=1+1-2=0`
`=>x_1=-1;x_2=-c/a=2`
`=>y_1=1;y_2=4`
`=>(-1;1), (2;4)` là giao điểm của `(P)` và `(d)`
`c)` Vì `(d') //// (d)=>a=1` và `b ne 2`
Thay `a=1;M(2;5)` vào `(d')` có:
`5=2+b<=>b=3` (t/m)
`=>` Ptr đường thẳng `(d'): y=x+3`
Trong mặt phẳng tọa độ Oxy, cho parabol (P) có phương trình và đường thẳng (d) có phương trình
1, trong đó m là tham số.
a, Vẽ parabol (P).
b, Xác định m để đường thẳng (d) cắt (P) tại hai điểm phân biệt.
c, Chứng minh rằng khi m thay đổi, các đường thẳng (d) luôn đi qua một điểm cố định Trong mặt phẳng tọa độ Oxy, cho parabol (P) có phương trình
và đường thẳng (d) có phương trình
1, trong đó m là tham số.
a, Vẽ parabol (P).
b, Xác định m để đường thẳng (d) cắt (P) tại hai điểm phân biệt.
c, Chứng minh rằng khi m thay đổi, các đường thẳng (d) luôn đi qua một điểm cố định
a:
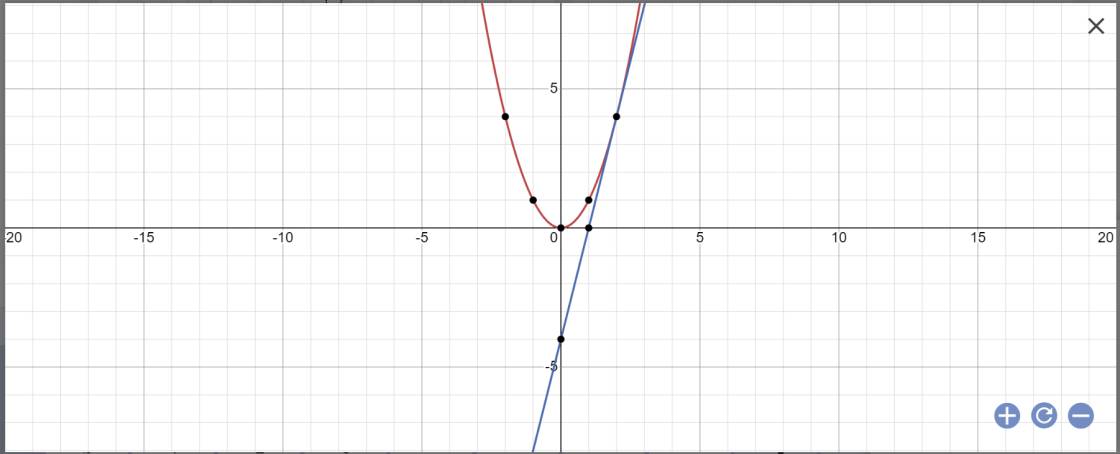
b: PTHĐGĐ là:
2x^2-(2m-2)x+m-1=0
Δ=(2m-2)^2-4*2*(m-1)
=4m^2-8m+4-8m+8
=4m^2-16m+12
=4m^2-2*2m*4+16-4=(2m-4)^2-4=(2m-6)(2m-2)
Để (d) cắt (P) tại 2 điểm pb thì (2m-6)(2m-2)>0
=>m>3 hoặc m<1
Trong mặt phẳng Oxy cho parabol (P) có phương trình y = 4 x 2 - 7 x + 3 . Phép đối xứng trục Oy biến (P) thành (P’) có phương trình:
A. y = 4 x 2 + 7 x - 3
B. y = 4 x 2 + 7 x + 3
C. y = - 4 x 2 + 7 x - 3
D. y = - 4 x 2 - 7 x + 3
Phép đối xứng trục Oy có:
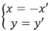
Thay vào phương trình (P) được y = 4 x ' 2 + 7 x ' + 3 hay y = 4 x 2 + 7 x + 3
Đáp án B
Trong mặt phẳng Oxy cho parabol (P) có phương trình: y = x 2 - 3 x + 1 . Phép đối xứng tâm I(4; -3) biến P thành (P’) có phương trình:
A. y = - x 2 + 13 x - 47
B. y = x 2 - 13 x + 47
C. y = - x 2 - 13 x - 47
D. y = - x 2 - 13 x + 47
Phép đối xứng tâm I biến M(x; y) thành M’(x’; y’) thì:
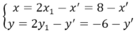
Thay vào phương trình (P) ta được:
- 6 - y ' = 8 - x ' 2 - 3 ( 8 - x ' ) + 1
⇒ - y ' = x ' 2 - 13 x ' + 47 hay
y = - x 2 + 13 x - 47
Đáp án A
1. Giải phương trình x (x - 1) (x2 - x + 1) = 6.
2. Trong mặt phẳng tọa độ Oxy, cho parabol (P): y=x2 và đường thẳng d: y = 2x - m +1
Gọi E và F là 2 diểm thuộc (P) có hoành độ lần lượt là -1 và 3. Xác định tọa độ E và F và viết phương trình đường thẳng đi qua 2 điểm E và F.
a. Giải phương trình $x^2 + x^4 - 6 = 0$.
b. Trong mặt phẳng tọa độ $Oxy$ cho đường thẳng $d:$ $y = 4x + 1 - m$ và parabol $(P):$ $y = x^2$. Tìm giá trị của $m$ để $d$ cắt $(P)$ tại hai điểm phân biệt có tung độ $y_1$ và $y_2$ sao cho $\sqrt{y_1}.\sqrt{y_2} = 5.$
Bài 1 :
Đặt \(x^2=t\left(t\ge0\right)\)khi đó phương trình tương đương
\(t+t^2-6=0\)
Ta có : \(\Delta=1+24=25\)
\(t_1=\frac{-1-5}{2}=-3;t_2=\frac{-1+5}{2}=2\)
TH1 : \(x^2=-3\)( vô lí )
TH2 : \(x^2=2\Leftrightarrow x=\pm\sqrt{2}\)
Vậy tập nghiệm của phương trình là S = { \(\pm\sqrt{2}\)}
a) \(x^2+x^4-6=0\)
Đặt \(x^2=t\left(t\ge0\right)\)
⇒ t + \(t^2\) - 6 = 0
⇒ \(t^2+t-6=0\)
⇒ Δ = \(1^2-4.\left(-6\right)\)
= 25
x1 = \(\dfrac{-1-5}{2}\) = - 3 (L)
x2 = \(\dfrac{-1+5}{2}\) = 2 (TM)
Thay \(x^2\) = 2 ⇒ x = \(\pm\sqrt{2}\)
Vậy x = \(\left\{\sqrt{2};-\sqrt{2}\right\}\)
b) (d) : y = 4x +1 - m
(p) : y = \(x^2\)
Xét phương trình hoành độ giao điểm
\(x^2=4x+1-m\)
⇒ \(x^2-4x+m-1=0\)
Δ' = 4 - m + 1
= 5 - m
Để (d) cắt (p) tại hai điểm phân biệt thì Δ' > 0
5 - m > 0
⇒ m < 5
Vậy m < 5 thì (d) cắt (p) tại hai điểm phân biệt
Gọi tọa độ giao điểm của (d) và (p) là (x1;y1) và (x2;y2)
Theo Vi-ét : \(\left\{{}\begin{matrix}S=x_1+x_2=4\\P=x_1x_2=m-1\end{matrix}\right.\)
và y1 = \(x_1^{2_{ }}\) ; y2 = \(x_2^2\)
Khi đó : \(\sqrt{y_1}.\sqrt{y_2}=5\) ⇒ \(\sqrt{y_1.y_2}=5\)
⇔ \(\sqrt{\left(x_1x_2\right)^2}=5\) ⇔ \(|m-1|=5\)
⇔ \(\left[{}\begin{matrix}m-1=5\\m-1=-5\end{matrix}\right.\) ⇔ \(\left[{}\begin{matrix}m=6\left(L\right)\\m=-4\left(TM\right)\end{matrix}\right.\)
Vậy m = - 4 thì TMĐKBT
a. Giải phương trình x^2 + x^4 - 6 = 0x
2
+x
4
−6=0.
b. Trong mặt phẳng tọa độ OxyOxy cho đường thẳng d:d: y = 4x + 1 - my=4x+1−m và parabol (P):(P): y = x^2y=x
2
. Tìm giá trị của mm để dd cắt (P)(P) tại hai điểm phân biệt có tung độ y_1y
1
và y_2y
2
sao cho \sqrt{y_1}.\sqrt{y_2} = 5.
y
1
.
y
2
=5.
Hướng dẫn giải:
a. Đặt x^2 = tx
2
=t, t \ge 0t≥0 thì phương trình đã cho trở thành:
t^2 + t - 6 = 0 \Leftrightarrow t^2 - 2t + 3t - 6 = 0 \Leftrightarrow (t-2)(t+3) = 0t
2
+t−6=0⇔t
2
−2t+3t−6=0⇔(t−2)(t+3)=0 \Leftrightarrow \left[\begin{aligned} & t = 2 \ \text{(thỏa mãn)} \\ & t = -3 \ \text{(loại)} \\ \end{aligned} \right.⇔[
t=2 (thỏa m
a
˜
n)
t=−3 (loại)
.
Với t = 2t=2 thì x^2 = 2 \Leftrightarrow x = \pm \sqrt 2.x
2
=2⇔x=±
2
.
Vậy phương trình có nghiệm x = \pm \sqrt2x=±
2
.
b. Phương trình hoành độ giao điểm: x^2 = 4x + 1 - mx
2
=4x+1−m \Leftrightarrow x^2 - 4x + m -1 = 0⇔x
2
−4x+m−1=0 (1)
\Delta' = 4 - m + 1 = 5 - mΔ
′
=4−m+1=5−m.
Để dd cắt (P)(P) tại hai điểm phân biệt thì phương trình (1) có 2 nghiệm phân biệt
\Leftrightarrow \Delta' > 0 \Leftrightarrow m < 5⇔Δ
′
>0⇔m<5.
Gọi hai giao điểm của dd và (P)(P) có tọa độ (x_1;y_1)(x
1
;y
1
) và (x_2;y_2)(x
2
;y
2
).
Ta có định lí Vi - et: \left\{\begin{aligned} & x_1 + x_2 = 4\\ & x_1x_2 = m-1 \end{aligned} \right.{
x
1
+x
2
=4
x
1
x
2
=m−1
và y_1 = x_1^2y
1
=x
1
2
; y_2 = x_2 ^2y
2
=x
2
2
.
Khi đó \sqrt{y_1}.\sqrt{y_2} = 5 \Leftrightarrow \sqrt{y_1.y_2} = 5
y
1
.
y
2
=5⇔
y
1
.y
2
=5
\Leftrightarrow \sqrt{(x_1x_2)^2} = 5 \Leftrightarrow |m-1| = 5⇔
(x
1
x
2
)
2
=5⇔∣m−1∣=5
\Leftrightarrow \left[\begin{aligned} & m - 1 = 5\\ & m - 1 = -5 \end{aligned} \right. \Leftrightarrow \left[\begin{aligned} & m = 6 \ \text{(loại)} \\ & m = -4 \ \text{(thỏa mãn)} \end{aligned} \right.⇔[
m−1=5
m−1=−5
⇔[
m=6 (loại)
m=−4 (thỏa m
a
˜
n)
.
Vậy với m = -4m=−4 thì dd cắt (P)(P) tại hai điểm phân biệt có tung độ y_1y
1
và y_2y
2
sao cho \sqrt{y_1}.\sqrt{y_2} = 5.
y
1
.
y
2
=5.
Trong mặt phẳng Oxy cho parabol (P) có phương trình y = x 2 - 3 x + 1 . Phép đối xứng tâm O(0;0) biến (P) thành (P’) có phương trình:
A. y = x 2 + 3 x - 1
B. y = - x 2 + 3 x + 1
C. y = - x 2 - 3 x - 1
D. y = - x 2 - 3 x + 1
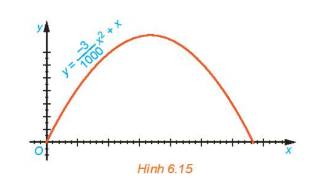
Quỹ đạo của vật được ném lên từ gốc O (được chọn là điểm ném) trong mặt phẳng tọa độ Oxy là một parabol có phương trình \(y = \frac{{ - 3}}{{1000}}{x^2} + x\) , trong đó x (mét) là khoảng cách theo phương ngang trên mặt đất từ vị trí của vật đến gốc O, y (mét) là độ cao của vật so với mặt đất (H.6.15)
a) Tím độ cao cực đại của vật trong quá trình bay
b) Tính khoảng cách từ điểm chạm mặt đất sau khi bay của vật đến gốc O. Khoảng cách này gọi là tầm xa của quỹ đạo.
a) Tung độ đỉnh của hàm số \(y = \frac{{ - 3}}{{1000}}{x^2} + x\) là:
\(\frac{{ - \Delta }}{{4a}} = \frac{{ - \left( {{1^2} - 4.\frac{{ - 3}}{{1000}}.0} \right)}}{{4.\frac{{ - 3}}{{1000}}}} = \frac{{250}}{3}\)
Vậy độ cao cực đại của vật là \(\frac{{250}}{3}(m)\)
b) Vật chạm đất khi:
\(y = 0 \Leftrightarrow \frac{{ - 3}}{{1000}}{x^2} + x = 0 \Leftrightarrow x = \frac{{1000}}{3}\)và x=0(loại)
Vậy khoảng cách từ điểm chạm mặt đất sau khi bay của vật đến gốc O là \(\frac{{1000}}{3}\left( m \right)\)
1) Giải hệ phương trình
\(\left\{{}\begin{matrix}\dfrac{3}{x-1}-\dfrac{2}{y+2}=4\\\dfrac{2x}{x-1}+\dfrac{1}{y+2}=5\end{matrix}\right.\)
2) Trong mặt phẳng tọa độ Oxy cho đường thẳng d : y = 3x + \(m^2\) -1 và parabol (P) : y = \(x^2\)
a) Chứng minh d luôn cắt (P) tại hai điểm phân biệt với mọi m.
b) Gọi \(x_1\) và \(x_2\) là hoành độ các giao điểm của d và (P). Tìm m để \(\left(x_1+1\right)\left(x_2+1\right)=1\)
Câu 1:
ĐKXĐ: \(\left\{{}\begin{matrix}x\ne1\\y\ne-2\end{matrix}\right.\)
Ta có: \(\left\{{}\begin{matrix}\dfrac{3}{x-1}-\dfrac{2}{y+2}=4\\\dfrac{2x}{x-1}+\dfrac{1}{y+2}=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3}{x-1}-\dfrac{2}{y+2}=4\\\dfrac{2x-2+2}{x-1}+\dfrac{1}{y+2}=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3}{x-1}-\dfrac{2}{y+2}=4\\\dfrac{2}{x-1}+\dfrac{1}{y+2}=3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{6}{x-1}-\dfrac{4}{y+2}=8\\\dfrac{6}{x-1}+\dfrac{3}{y+2}=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{-7}{y+2}=-1\\\dfrac{6}{x-1}+\dfrac{3}{y+2}=9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y+2=7\\\dfrac{6}{x-1}+\dfrac{3}{7}=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=5\\\dfrac{6}{x-1}=\dfrac{60}{7}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-1=\dfrac{7}{10}\\y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{17}{10}\left(nhận\right)\\y=5\left(nhận\right)\end{matrix}\right.\)
Vậy: Hệ phương trình có nghiệm duy nhất là \(\left(x,y\right)=\left(\dfrac{17}{10};5\right)\)
Câu 2:
a) Phương trình hoành độ giao điểm của (P) và (d) là:
\(x^2=3x+m^2-1\)
\(\Leftrightarrow x^2-3x-m^2+1=0\)
\(\Delta=\left(-3\right)^2-4\cdot1\cdot\left(-m^2+1\right)\)
\(=9-4\left(-m^2+1\right)=9+4m^2-4=4m^2+5>0\forall m\)
Vậy: (d) luôn cắt (P) tại hai điểm phân biệt với mọi m