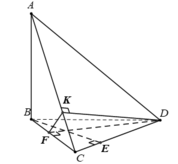
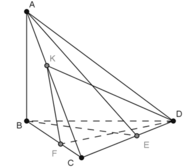
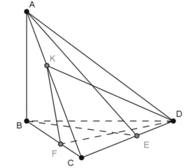
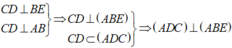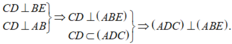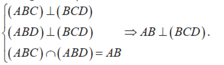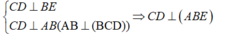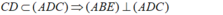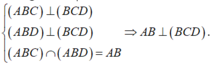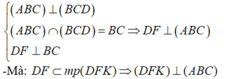Cho tứ diện ABCD có AB⊥(BCD). Trong ΔBCD vẽ các đường cao BE và DF cắt nhau ở O. Trong mp(ADC), vẽ DK⊥AC tại K. Chứng minh: (ADC)⊥(DFK)

Những câu hỏi liên quan
Cho tứ diện ABCD có AB⊥(BCD) . Trong ΔBCD vẽ các đường cao BE và DF cắt nhau ở O. Trong (ADC) vẽ DK⊥AC tại K. Chứng minh: (ADC)⊥(DFK)
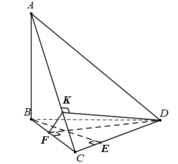
Ta có:
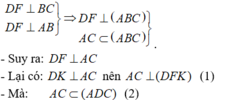
- Từ (1) và (2) suy ra: (ADC) ⊥ (DFK).
Đúng 0
Bình luận (0)
Cho tứ diện ABCD có AB⊥(BCD). Trong ΔBCD vẽ các đường cao BE và DF cắt nhau ở O. Trong mp(ADC), vẽ DK⊥AC tại K. Chứng minh: (ADC)⊥(ABE)
Phần II: Tự luận
Cho tứ diện ABCD có AB⊥(BCD) . Trong ΔBCD vẽ các đường cao BE và DF cắt nhau ở O. Trong (ADC) vẽ DK⊥AC tại K. Chứng minh: (ADC)⊥(ABE)
Cho tứ diện ABCD có AB ⊥(BCD). Trong tam giác BCD vẽ các đường cao BE và DF cắt nhau tại O. Trong mp(ACD) vẽ DK ⊥AC. Gọi H là trực tâm của tam giác ACD.
a. Chứng minh: (ACD)⊥(ABE) và (ACD)⊥ (DFK).
b. Chứng minh: OH⊥(ACD)
a/ \(AB\perp\left(BCD\right)\Rightarrow AB\perp CD\)
Mà \(BE\perp CD\Rightarrow CD\perp\left(ABE\right)\)
\(CD\in\left(ACD\right)\Rightarrow\left(ACD\right)\perp\left(ABE\right)\)
*/ \(AB\perp\left(BCD\right)\Rightarrow AB\perp DF\)
\(DF\perp BC\Rightarrow DF\perp\left(ABC\right)\Rightarrow DF\perp AC\)
Mà \(AC\perp DK\Rightarrow AC\perp\left(DFK\right)\Rightarrow\left(ACD\right)\perp\left(DFK\right)\)
b/ H là trực tâm ACD \(\Rightarrow CD\perp AH\)
Mà \(CD\perp AB\Rightarrow CD\perp\left(ABE\right)\)
\(\Rightarrow CD\perp OH\)
Theo câu a ta có \(AC\perp\left(DFK\right)\Rightarrow AC\perp OH\)
\(\Rightarrow OH\perp\left(ACD\right)\)
Đúng 0
Bình luận (0)
Tứ diện ABCD có AB bot left( {BCD} right). Trong tam giác BCD vẽ đường cao BE và DF cắt nhau tại O. Trong mặt phẳng left( {ACD} right) vẽ {rm{D}}K vuông góc với AC tại K. Gọi H là trực tâm của tam giác ACD. Chứng minh rằng:a) left( {ADC} right) bot left( {ABE} right) và left( {ADC} right) bot left( {DFK} right);b) OH bot left( {ADC} right).
Đọc tiếp
Tứ diện \(ABCD\) có \(AB \bot \left( {BCD} \right)\). Trong tam giác \(BCD\) vẽ đường cao \(BE\) và \(DF\) cắt nhau tại \(O\). Trong mặt phẳng \(\left( {ACD} \right)\) vẽ \({\rm{D}}K\) vuông góc với \(AC\) tại \(K\). Gọi \(H\) là trực tâm của tam giác \(ACD\). Chứng minh rằng:
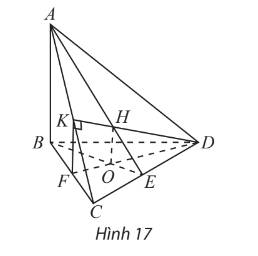
a) \(\left( {ADC} \right) \bot \left( {ABE} \right)\) và \(\left( {ADC} \right) \bot \left( {DFK} \right)\);
b) \(OH \bot \left( {ADC} \right)\).
a) Ta có:
\(\left. \begin{array}{l}AB \bot \left( {BC{\rm{D}}} \right) \Rightarrow AB \bot C{\rm{D}}\\BE \bot CE\end{array} \right\} \Rightarrow C{\rm{D}} \bot \left( {ABE} \right)\)
Lại có \(C{\rm{D}} \subset \left( {A{\rm{D}}C} \right)\)
Vậy \(\left( {ADC} \right) \bot \left( {ABE} \right)\)
\(\begin{array}{l}\left. \begin{array}{l}AB \bot \left( {BC{\rm{D}}} \right) \Rightarrow AB \bot DF\\DF \bot BC\end{array} \right\} \Rightarrow DF \bot \left( {ABC} \right)\\\left. \begin{array}{l} \Rightarrow DF \bot AC\\DK \bot AC\end{array} \right\} \Rightarrow AC \bot \left( {DFK} \right)\end{array}\)
Lại có \(AC \subset \left( {A{\rm{D}}C} \right)\)
Vậy \(\left( {ADC} \right) \bot \left( {DFK} \right)\)
b) Ta có:
\(\left. \begin{array}{l}\left( {ADC} \right) \bot \left( {ABE} \right)\\\left( {ADC} \right) \bot \left( {DFK} \right)\\\left( {ABE} \right) \cap \left( {DFK} \right) = OH\end{array} \right\} \Rightarrow OH \bot \left( {ADC} \right)\)
Đúng 0
Bình luận (0)
cho tứ diện ABCD có 2 mặt ABC, ABD vuông góc với đáy DBC , vẽ có đường cao BE , DF của tam giác BCD, đường cao DK của tam giác ACD
a) chứng minh AB vuông góc với (BCD)
b) Chứng minh 2 mặt phẳng (ABE) và (DFK) vuông góc với (ADC)
\(\left\{{}\begin{matrix}\left(ABD\right)\perp\left(BCD\right)\\\left(ABC\right)\perp\left(BCD\right)\\\left(ABC\right)\cap\left(ABD\right)=AB\end{matrix}\right.\) \(\Rightarrow AB\perp\left(BCD\right)\)
b/ \(AB\perp\left(BCD\right)\Rightarrow AB\perp CD\)
Mà \(BE\perp CD\Rightarrow CD\perp\left(ABE\right)\)
\(CD\in\left(ACD\right)\Rightarrow\left(ACD\right)\perp\left(ABE\right)\)
*/ \(\left\{{}\begin{matrix}AB\perp\left(BCD\right)\Rightarrow AB\perp DF\\DF\perp BC\end{matrix}\right.\) \(\Rightarrow DF\perp\left(ABC\right)\Rightarrow DF\perp AC\)
Mà \(DK\perp AC\Rightarrow AC\perp\left(DFK\right)\)
\(AC\in\left(ACD\right)\Rightarrow\left(ACD\right)\perp\left(DFK\right)\)
Đúng 0
Bình luận (0)
Cho tứ diện ABCD có hai mặt phẳng (ABC) và (ABD) cùng vuông góc với (BCD). Gọi BE và DF là hai đường cao của tam giác BCD, DK là đường cao của tam giác ACD. Chứng minh (ABE)⊥(ADC)
Cho ∆ABC nhọn (ABAC) nội tiếp đường tròn tâm O bán kính R, 3 đường cao AD, BE và CF cắt nhau tại Ha) Chứng minh các tứ giác AEHF, AEDB nội tiếp.b) Vẽ đường kính AK của đường tròn tâm O.Chứng minh AB . AC 2R . ADc) BE cắt (O) ở Q, CF cắt (O) tại P.Chứng minh AP AQ Và H đối xứng với P qua AB.d) Chứng minh OC vuông góc với PE. Các bạn giúp mình với, tối nay mình phải nộp cho thầy rồi
Đọc tiếp
Cho ∆ABC nhọn (AB<AC) nội tiếp đường tròn tâm O bán kính R, 3 đường cao AD, BE và CF cắt nhau tại H
a) Chứng minh các tứ giác AEHF, AEDB nội tiếp.
b) Vẽ đường kính AK của đường tròn tâm O.
Chứng minh AB . AC = 2R . AD
c) BE cắt (O) ở Q, CF cắt (O) tại P.
Chứng minh AP = AQ Và H đối xứng với P qua AB.
d) Chứng minh OC vuông góc với PE.
Các bạn giúp mình với, tối nay mình phải nộp cho thầy rồi
a: góc AEH+góc AFH=180 độ
=>AEHF nội tiếp
góc AEB=góc ADB=90 độ
=>AEDB nội tiếp
b: góc ACK=góc ABK=1/2*sđ cung AK=90 độ
Xét ΔACK vuông tại C và ΔADB vuông tại D có
góc AKC=góc ABD
=>ΔACK đồng dạng với ΔADB
=>AC/AD=AK/AB
=>AC*AB=AD*AK=AD*2R
Đúng 0
Bình luận (0)
Cho tứ diện ABCD có hai mặt phẳng (ABC) và (ABD) cùng vuông góc với (BCD). Gọi BE và DF là hai đường cao của tam giác BCD, DK là đường cao của tam giác ACD. Chứng minh (ABC)⊥(DFK)