Số nghiệm chung của hai phương trình 4 cos 2 x - 3 = 0 và 2 sin x + 1 = 0 trên khoảng - π 2 ; 3 π 2 là:
A. 4.
B. 1.
C. 2
D. 3.
Câu 33 : số nghiệm của phương trình 3cos x + 2=0 trên đoạn [0;5π] là: A. 4 B. 3 C. 6 D. 5 Câu 34. Số nghiệm của phương trình ( 2cos^2 x - cos x)/ (tan x -√3)=0 trên đoạn [0;3] là A. 4 B. 3 C. 2 D. 1
Cho tập hợp A={-3;1;2;3} và ba phương trình:
(x-1)2+(x-2)2 = 1 (1)
x4-3x3+3x2-3x+2=0 (2)
x3-7x+6=0 (3)
Số nào thuộc A là nghiệm, không là nghiệm của mỗi phương trình là nghiệm chung của hai trong ba phương trình, là nghiệm chung của cả ba phương trình.
Tìm số nghiệm của phương trình cos 2x - cos x - 2 = 0, x ∈ 0 , 2 π
A. 0
B. 2
C. 1
D. 3
Số nghiệm chung của hai phương trình 4 cos 2 x − 3 = 0 và 2.sin x + 1 = 0 trên khoảng − π 2 ; 3 π 2 là:
A. 4
B. 1
C. 2
D. 3
Cho hai phương trình: x2-5x+6=0 (1)
x+(x-2)(2x+1)=2 (2)
a) Chứng minh hai phương trình có nghiệm chung là x=2
b) Chứng minh: x=3 là nghiệm của (1) nhưng không là nghiệm của (2).
c) Hai phương trình đã cho có tương đương với nhau không, vì sao?
a:
Thay x=2 vào (1), ta được:
\(2^2-5\cdot2+6=0\)(đúng)
Thay x=2 vào (2), ta được:
\(2+\left(2-2\right)\cdot\left(2\cdot2+1\right)=2\)(đúng)
b: (1)=>(x-2)(x-3)=0
=>S1={2;3}
(2)=>\(x+2x^2+x-4x-2-2=0\)
\(\Leftrightarrow x^2+x-2=0\)
=>(x+2)(x-1)=0
=>S2={-2;1}
vậy: x=3 là nghiệm của (1) nhưng không là nghiệm của (2)
Cho hai phương trình cos 3x -1 =0 (1); cos 2x = - 1 2 (2) Tập các nghiệm của phương trình (1) đồng thời là nghiệm của phương trình (2) là
![]()
![]()
![]()
![]()
Đáp án D
Ta có
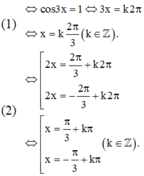
Suy ra nghiệm chung của hai phương trình là
![]()
Nghiệm của phương trình \(sin^4x+cos^4x+cos\left(x-\dfrac{\pi}{4}\right).sin\left(3x-\dfrac{\pi}{4}\right)-\dfrac{3}{2}=0\)
\(\Leftrightarrow\left(sin^2x+cos^2x\right)^2-2sin^2x.cos^2x+\dfrac{1}{2}sin\left(4x-\dfrac{\pi}{2}\right)+\dfrac{1}{2}sin2x-\dfrac{3}{2}=0\)
\(\Leftrightarrow1-\dfrac{1}{2}sin^22x-\dfrac{1}{2}cos4x+\dfrac{1}{2}sin2x-\dfrac{3}{2}=0\)
\(\Leftrightarrow1-\dfrac{1}{2}\left(\dfrac{1-cos4x}{2}\right)-\dfrac{1}{2}cos4x+\dfrac{1}{2}sin2x-\dfrac{3}{2}=0\)
\(\Leftrightarrow-\dfrac{3}{4}-\dfrac{1}{4}cos4x+\dfrac{1}{2}sin2x=0\)
\(\Leftrightarrow-\dfrac{3}{4}-\dfrac{1}{4}\left(1-2sin^22x\right)+\dfrac{1}{2}sin2x=0\)
\(\Leftrightarrow...\)
Cho hai phương trình:
\(x^3+3x^2+2x=0\) và \(\left(x+1\right)\left(x^2+2x+1+a\right)=0\) (với x là ẩn số). Tìm các giá trị của a để hai phương trình trên chỉ có một nghiệm chung duy nhất
\(x^3+3x^2+2x=0\Rightarrow x\left(x+1\right)\left(x+2\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x=-1\\x=-2\end{matrix}\right.\)
\(\left(x+1\right)\left(x^2+2x+1+a\right)=0\Rightarrow\left[{}\begin{matrix}x=-1\\x^2+2x+1=-a\end{matrix}\right.\)
Vì 2 pt đã có nghiệm chung là \(-1\Rightarrow\) nghiệm của pt \(\left(x+1\right)^2=-a\) phải khác \(0,2\)
\(\Rightarrow a\ne-1;-9\)
(cách mình là vậy chứ mình cũng ko chắc là có đúng ko nữa)
\(x^3+3x^2+2x=0\left(1\right)\)
\(\Leftrightarrow x\left(x^2+3x+2\right)=0\)
\(\Leftrightarrow x\left(x^2+x+2x+2\right)=0\)
\(\Leftrightarrow x\left[x\left(x+1\right)+2\left(x+1\right)\right]=0\)
\(\Leftrightarrow x\left(x+2\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x+2=0\\x+1=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=-1\end{matrix}\right.\)
Vậy phương trình (1) có nghiệm \(x=0;x=-2;x=-1\)
\(\Leftrightarrow\left(x+1\right)\left(x^2+2x+1+a\right)=0\left(2\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}x+1=0\Leftrightarrow x=-1\\x^2+2x+1+a=0\end{matrix}\right.\)
\(\Rightarrow x=-1\) là (1) nghiệm của phương trình (2)
Đặt \(F\left(x\right)=\left(x+1\right)\left(x^2+2x+1+a\right)\)
Có phương trình (1) và (2) có nghiệm chung là =1
Để (1) và (2) có 1 nghiệm chung duy nhất
Thì \(\left\{{}\begin{matrix}F\left(0\right)\ne0\\F\left(-2\right)\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}1.\left(1+a\right)\ne0\\\left(-2+1\right)\left(4-4+1+a\right)\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a\ne-1\\-\left(a+1\right)\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a\ne-1\\a\ne-1\end{matrix}\right.\)
-Chúc bạn học tốt-