Cho tam giác ABC vuông tại A, đường cao AH. Kẻ He vuông góc với AB (E ∈ AB); kẻ HF vuông góc với AC (F ∈ AC)
a) Chứng minh: Tứ giác AEHF là hình chữ nhật
b) Gọi P là điểm đối xứng của H qua AB . Tứ giác APEF là hình gì? Vì sao?

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A, đường cao AH. Kẻ HE vuông góc với AB tại E, Kẻ HF vuông góc với AC tại F. Chứng minh tứ giác BEFC nội tiếp
Gợi ý: A F E ^ = A H E ^ (tính chất hình chữ nhật và A H E ^ = A B H ^ (cùng phụ B H E ^ )
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH. Kẻ HE vuông góc với AB tại E, Kẻ HF vuông góc với AC tại F. Chứng minh tứ giác BEFC nội tiếp.
Ta có: \(\widehat{C_1}=\widehat{A_1}\)(cùng phụ với \(\widehat{B_1}\)) \(\left(1\right)\)
Xét tứ giác AEHF có: \(\widehat{A}=\widehat{E}=\widehat{F}=\widehat{H}=90^o\)
=> tứ giác AEHF là h.c.n
=> \(\widehat{A_1}=\widehat{E_1}\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\widehat{E_1}=\widehat{C_1}\)
vì \(\widehat{E_1}+\widehat{BEF}=180^o\)
\(\Rightarrow\widehat{C_1}+\widehat{BEF}=180^o\) mà 2 góc đối nhau
=> tứ giác BEFC nội tiếp
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A đường cao AH kẻ HD vuông góc với AB tại D và HE vuông góc với AC tại E Chứng minh AH.AH = AD.DB + AE.EC
\(\widehat{DAH}=90^0-\widehat{AHD}=\widehat{BHD}\).
\(\widehat{HAE}=90^0-\widehat{AHE}=\widehat{CHE}\).
-△AHD và △HBD có: \(\widehat{DAH}=\widehat{DHB};\widehat{ADH}=\widehat{BDH}=90^0\).
\(\Rightarrow\)△AHD∼△HBD (g-g) \(\Rightarrow\dfrac{AD}{HD}=\dfrac{HD}{BD}\Rightarrow HD^2=AD.BD\).
-△AHE và △HCE có: \(\widehat{HAE}=\widehat{CHE};\widehat{AEH}=\widehat{HEC}=90^0\).
\(\Rightarrow\)△AHE∼△HCE (g-g) \(\Rightarrow\dfrac{AE}{HE}=\dfrac{HE}{CE}\Rightarrow HE^2=AE.CE\)
\(\Rightarrow HD^2+HE^2=AD.BD+AE.CE\left(1\right)\).
-Tứ giác ADHE có: \(\widehat{ADH}=\widehat{DAE}=\widehat{AEH}=90^0\)
\(\Rightarrow\)ADHE là hình chữ nhật nên △DHE vuông tại H, \(AH=DE\)
\(\Rightarrow HD^2+HE^2=DE^2=AH^2\left(2\right)\)
-Từ (1), (2) suy ra: \(AH^2=AD.BD+AE.CE\)
Đúng 0
Bình luận (0)
Cho tam giác ABC, AB=5cm,AC=12cm,BC=13cm. AH là đường cao tam giác ABC và AH vuông góc với BC
a, Chứng minh: Tam giác ABC là tam giác vuông và tính AH
b, Kẻ HE vuông góc với AB tại E và HF vuông góc với AC tại F. Chứng minh: AE.AB=AF.AC
c, Tam giác AEF đồng dạng tam giác ABC
d,\(\dfrac{EB}{FC}=(\dfrac{AB}{AC})^{3}\)
e, BC.BE.CF=\(AH^{3}\)
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH=\dfrac{60}{13}\left(cm\right)\)
b: Xét ΔABH vuông tại H có HE là đường cao ứng với cạnh huyền AB
nên \(AE\cdot AB=AH^2\left(1\right)\)
Xét ΔACH vuông tại H có HF là đường cao ứng với cạnh huyền AC
nên \(AF\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)
Đúng 1
Bình luận (0)
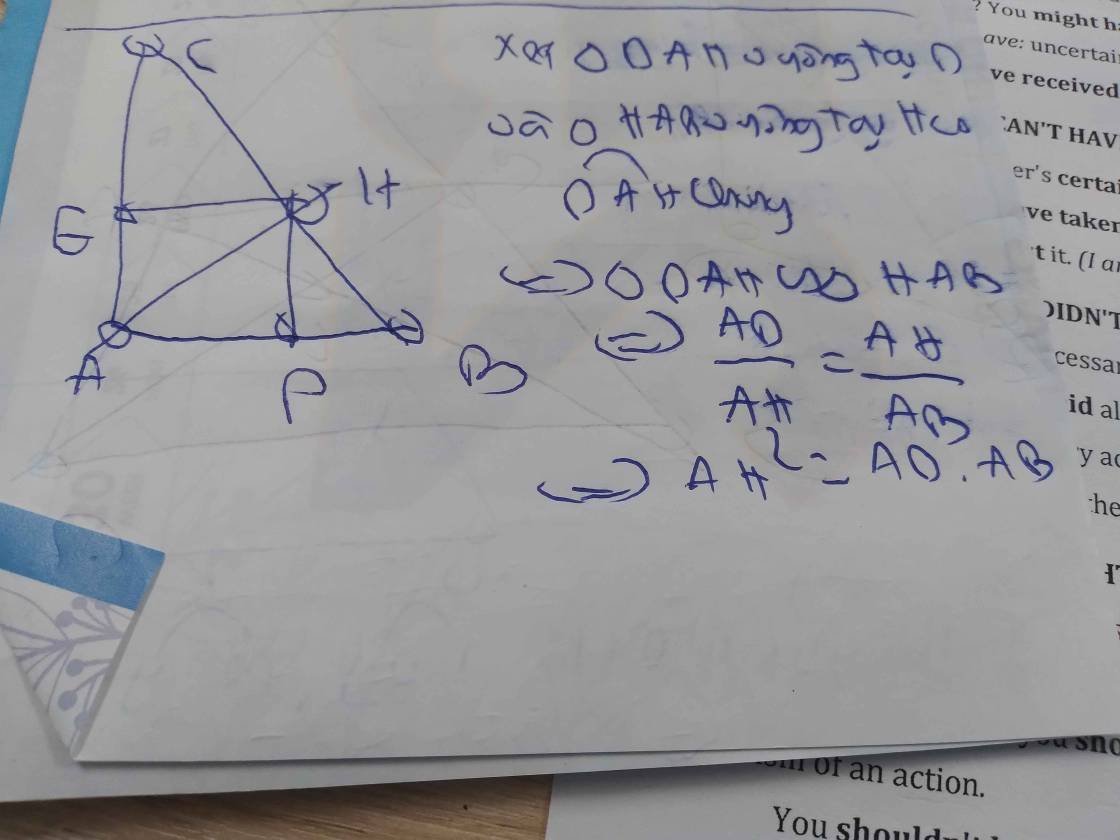
cho tam giác ABC vuông tại A có AH là đường cao. Kẻ HD vuông góc với AB; HE vuông góc với AC (D thuộc AB; E thuộc AC) CHỨNG MINH AH2= AD.AB
cho tam giác nhọn ABC, kẻ đường cao AH. từ H kẻ HE vuông góc với AB tại E, kẻ HF vuông góc với AC tại F.
a)chứng minh: tam giác AEH đồng dạng với tam giác AHB
Xét tam giác AEH và tam giác AHB, có:
\(\widehat{AHB}=\widehat{AEH}=90^0\)
\(\widehat{A}:chung\)
Vậy tam giác AEH đồng dạng tam giác AHB ( g.g )
Đúng 3
Bình luận (0)
cho tam giác ABC vuông tại A đường cao AH kẻ HD vuông góc với AB tại D kẻ HE vuông góc với AC tại E a chứng minh tứ giác ADHE là hình chữ nhật b chứng minh AH=DE? c tam giác ABC cần có điều kiện gì thì tứ giác ADHE là hình vuông
a: Xét tứ giác ADHE có
góc ADH=góc AEH=góc DAE=90 độ
nên ADHE là hình chữ nhật
b: ADHE là hình chữ nhật
nen AH=DE
c: Để ADHE là hình vuông thì AH là phân giác của góc DAE
=>ΔABC cân tại A
=>AB=AC
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có đường cao AH, lấy E bất kỳ trên AB, kẻ HF vuông góc với HE (F€AC). CMR HE*BC=EF*AB
Cho tam giác abc vuông tại a,bc=5cm,°C=30°
a)giải tam giác vuông ABC.
b)tính đường cao AH
c)kẻ HE vuông góc AB TẠI E VÀ HF VUÔNG GÓC AC TẠI F CM :AH\3=BE.CF.BC cần gấp 

Câu 15:
a: ĐKXĐ: x>=0; x<>1
Đúng 0
Bình luận (0)
Bài 5 : Cho tam giác ABC vuông tại A có đường cao AH , kẻ HE vuông góc AB tại E và HD vuông góc AC tại D. Chứng minh
a) AE . AB = AD.AC
b) AH.(tanB + tanC ) = BC
a: Xét ΔAHB vuông tại H có HE là đường cao
nên \(AE\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HD là đường cao
nên \(AD\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AB=AD\cdot AC\)
Đúng 0
Bình luận (0)