Cho hàm số f ( x ) = x 3 + 3 x 2 - m . Tìm các giá trị của m để đồ thị hàm số f(x) cắt trục hoành tại 3 điểm phân biệt
A. m ≤ 0 m ≥ 4
B. m ∈ 0 ; 4
C. m < 0 m > 4
D. m ∈ 0 ; 4
Câu 1: Cho hàm số y = 2x\(^2\)
a) Hãy lập bảng tính các giá trị f(-5), f(-3), f(0), f(3), f(5)
b) Tìm x biết f(x) = 8, f(x) = 6 - 4\(\sqrt{2}\)
Câu 2: Cho hàm số y = f(x) = \(\dfrac{1}{3}x^2\)
Tìm các giá trị của x, biết rằng \(y=\dfrac{1}{27}\). Cũng câu hỏi tương tự với y = 5
Câu 1:
a)
| \(y=f\left(x\right)=2x^2\) | -5 | -3 | 0 | 3 | 5 |
| f(x) | 50 | 18 | 0 | 18 | 50 |
b) Ta có: f(x)=8
\(\Leftrightarrow2x^2=8\)
\(\Leftrightarrow x^2=4\)
hay \(x\in\left\{2;-2\right\}\)
Vậy: Để f(x)=8 thì \(x\in\left\{2;-2\right\}\)
Ta có: \(f\left(x\right)=6-4\sqrt{2}\)
\(\Leftrightarrow2x^2=6-4\sqrt{2}\)
\(\Leftrightarrow x^2=3-2\sqrt{2}\)
\(\Leftrightarrow x=\sqrt{3-2\sqrt{2}}\)
hay \(x=\sqrt{2}-1\)
Vậy: Để \(f\left(x\right)=6-4\sqrt{2}\) thì \(x=\sqrt{2}-1\)
Cho các hàm số \(f\left(x\right)=x^2-4x+m\) và \(g\left(x\right)=\left(x^2+1\right)\left(x^2+2\right)^2\left(x^2+3\right)^3\) . Tìm tập hợp tất cả các giá trị của tham số m để hàm số \(g\left(f\left(x\right)\right)\) đồng biến trên \(\left(3;+\infty\right)\) .
\(g'\left(x\right)=0\Rightarrow x=0\)
Ta thấy \(g\left(x\right)\) đồng biến trên \(\left(0;+\infty\right)\)
\(\Rightarrow g\left(f\left(x\right)\right)\) đồng biến khi \(f\left(x\right)\ge0\)
\(\Rightarrow g\left(f\left(x\right)\right)\) đồng biến trên \(\left(3;+\infty\right)\) khi \(f\left(x\right)\ge0\) ; \(\forall x>3\)
\(\Leftrightarrow x^2-4x\ge-m\) ; \(\forall x>3\)
\(\Leftrightarrow-m\le\min\limits_{x>3}\left(x^2-4x\right)\)
\(\Rightarrow-m\le-3\Rightarrow m\ge3\)
1) Cho hàm số y = f(x) = 2x - 3.
a) Tính f(2); f(0); f(-3); f(![]() )
)
b) Tìm giá trị của x để f(x) = 5
c) Trong hai điểm M(0; -3); N(3; 1), điểm nào thuộc đồ thị hàm số trên?
2)
a) Vẽ hệ trục tọa độ Oxy và đánh dấu các điểm A(2; -2); B(-3;1/2); C(0; 2); D(-3; 0)
3) Vẽ đồ thị của hàm số y = 2x và y = - 1/2x trên cùng một hệ trục tọa độ.
Cho hàm số f(x) có đạo hàm là hàm f'(x). Đồ thị hàm số f'(x) như hình vẽ bên. Biết rằng f(0) + f(1) - 2f(2) = f(4) - f(3). Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của f(x) trên đoạn [0;4].

A. m = f(4), M = f(2)
B. m = f(1), M = f(2)
C. m = f(4), M = f(1)
D. m = f(0), M = f(2)
Chọn A
Dựa vào đồ thị của hàm f'(x) ta có bảng biến thiên.
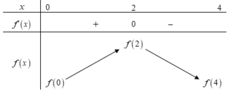
Vậy giá trị lớn nhất M = f(2)
Hàm số đồng biến trên khoảng (0;2) nên f(2) > f(1) => f(2) - f(1) > 0 .
Hàm số nghịch biến trên khoảng (2;4) nên f(2) > f(3) => f(2) - f(3) > 0.
Theo giả thuyết: f(0) + f(1) - 2f(2) = f(4) - f(3).
![]()
=> f(0) > f(4)
Vậy giá trị nhỏ nhất m = f(4)
cho hàm số f(x)=\(\begin{cases} \sqrt{2x-4}+3 \\ \dfrac{x+2}{x^2-2mx+m^2+2} \end{cases} \)(trên) khi x≥2, (dưới) khi x<2. Tìm các giá trị của tham số thực m để hàm số liên tục trên R
\(\lim\limits_{x\rightarrow2^+}f\left(x\right)=\lim\limits_{x\rightarrow2^+}\sqrt{2x-4}+3\)
\(=\sqrt{2\cdot2-4}+3=3\)
\(f\left(2\right)=\sqrt{2\cdot2-4}+3=0+3=3\)
\(\lim\limits_{x\rightarrow2^-}f\left(x\right)=\lim\limits_{x\rightarrow2^-}\dfrac{x+2}{x^2-2mx+m^2+2}\)
\(=\dfrac{2+2}{2^2-2m\cdot2+m^2+2}=\dfrac{4}{m^2-4m+6}\)
Để hàm số f(x) liên tục trên R thì f(x) liên tục tại x=2
=>\(\dfrac{4}{m^2-4m+6}=3\)
=>\(4=3\left(m^2-4m+6\right)\)
=>\(3m^2-12m+18-4=0\)
=>\(3m^2-12m+14=0\)
\(\Leftrightarrow3m^2-12m+12+2=0\)
=>\(3\left(m-2\right)^2+2=0\)(vô lý)
=>\(m\in\varnothing\)
Cho hàm số ( ) ( )2 2 1 2 1f x x m x m= − − − + − . Tìm tất cả các giá trị của tham số m để ( ) 0f x >Cho hàm số \(f\left(x\right)=-x^2-2\left(m-1\right)x+2m-1\). Tìm tất cả các giá trị của tham số \(m\) để \(f\left(x\right)>0,\forall x\in\left(0;1\right)\).
, ( )Cho hàm số ( ) ( )2 2 1 2 1f x x m x m= − − − + − . Tìm tất cả các giá trị của tham số m để ( ) 0f x >, ( )
Ta có \(f\left(x\right)>0,\forall x\in\left(0;1\right)\)
\(\Leftrightarrow-x^2-2\left(m-1\right)x+2m-1>0,\forall x\left(0;1\right)\)
\(\Leftrightarrow-2m\left(x-1\right)>x^2-2x+1,\forall x\in\left(0;1\right)\) (*)
Vì \(x\in\left(0;1\right)\Rightarrow x-1< 0\) nên (*) \(\Leftrightarrow-2m< \dfrac{x^2-2x+1}{x-1}=x-1=g\left(x\right),\forall x\in\left(0;1\right)\)
\(\Leftrightarrow-2m\le g\left(0\right)=-1\Leftrightarrow m\ge\dfrac{1}{2}\)
Cho hàm số y=f(x) có đồ thị như hình vẽ bên dưới: Tìm tất cả các giá trị của tham số m để đồ thị hàm số h ( x ) = f 2 ( x ) + f ( x ) + m có đúng 3 điểm cực trị.
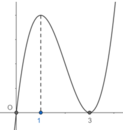
A. m ≤ 1
B. m > 1 4
C.m<1
D. m ≥ 1 4
Cho hàm số f(x) = \(\dfrac{x^3}{3}-mx^2+\left(m+2\right)x+3\). Có tất cả các giá trị nguyên của tham số m để f'(x) ≥ 0 với mọi thuộc R.
: Cho hàm số y = f(x) = -2x + 3.
a) Tính f(-2); f(0); f(-\(\dfrac{1}{2}\)). b) Tìm các giá trị của x biết : f(x) = 5 ; f(x) = 1
a) Cho hàm số y = f(x) = -2x + 3.
Ta có: f(-2)= -2.(-2)+3
= 4+3=7
Ta có: f(0)= -2.0+3
= 0+3=3
Ta có: f(
Lời giải:
a.
$f(-2)=(-2)(-2)+3=7$
$f(0)=(-2).0+3=3$
$f(\frac{-1}{2})=(-2).\frac{-1}{2}+3=4$
b.
$f(x)=-2x+3=5$
$\Rightarrow -2x=2$
$\Rightarrow x=-1$
$f(x)=-2x+3=1$
$\Rightarrow -2x=1-3=-2$
$\Rightarrow x=1$